Factoring Dividing Out Divide OUT The LARGEST NUMBER

Factoring: Dividing Out • Divide OUT: – The LARGEST NUMBER you can divide ALL terms by – The SMALLEST POWER of a variable that exists in ALL terms • What you can divide out is a factor in front of () • What remains when you divide out is a factor inside the () • Check to see if the () can be factored more

Examples: Dividing Out • 1. 2 x⁵- 18 x² • 2. 3 x³ - 12 x² + 15 x • 3. 2 x⁴ - 18 x³

Factoring: Difference of Squares • 2 terms • SUBTRACTION • Both terms have nice square roots (may need to divide out first). • Create 2 Factors – Square root of first term FIRST in each factor – Square root of second term SECOND in each factor – Each factor has a different operation between terms – (√first + √second)(√first - √second)

Examples: Difference of Squares • 1. x² - 49 • 2. 1 – 25 x² • 3. 4 x² - 16 • 4. 16 x² - 625

Examples: Divide Out & Difference of Squares • 1. 2 x⁵ - 18 x³ • 2. 27 x³ - 3 x • 3. 3 x⁵ - 75 x³

Factoring by Grouping 4 TERMS Separate into 2 Groups of 2 terms Divide out of first pair Divide out of second pair so the () has the SAME factor as the first pair did. • Create 2 factors • • – The SHARED FACTOR of the 2 groups – What was divided out of each pair • Check to see if either factor can be factored more!

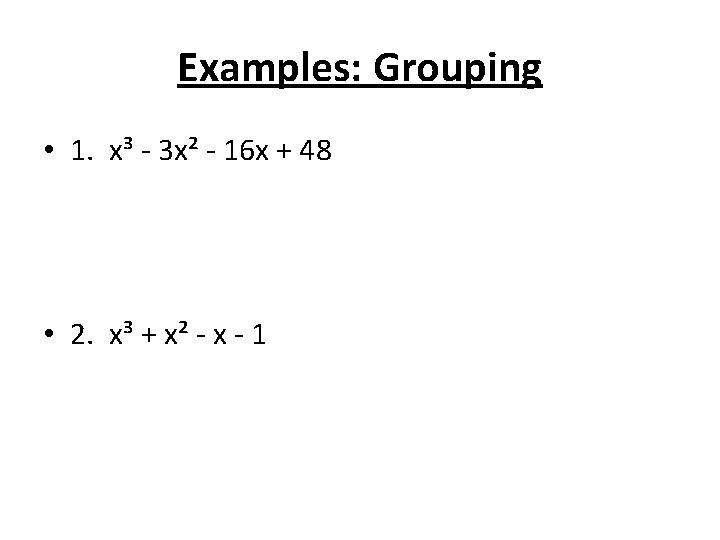
Examples: Grouping • 1. x³ - 3 x² - 16 x + 48 • 2. x³ + x² - x - 1

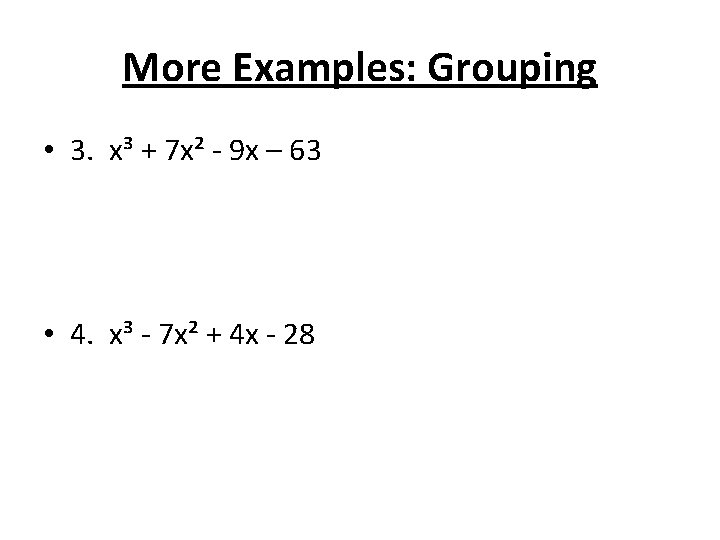
More Examples: Grouping • 3. x³ + 7 x² - 9 x – 63 • 4. x³ - 7 x² + 4 x - 28