FACTORING BY GROUPING MM 1 A 2 f

FACTORING BY GROUPING MM 1 A 2 f: FACTOR Essential Question: What are my roots?

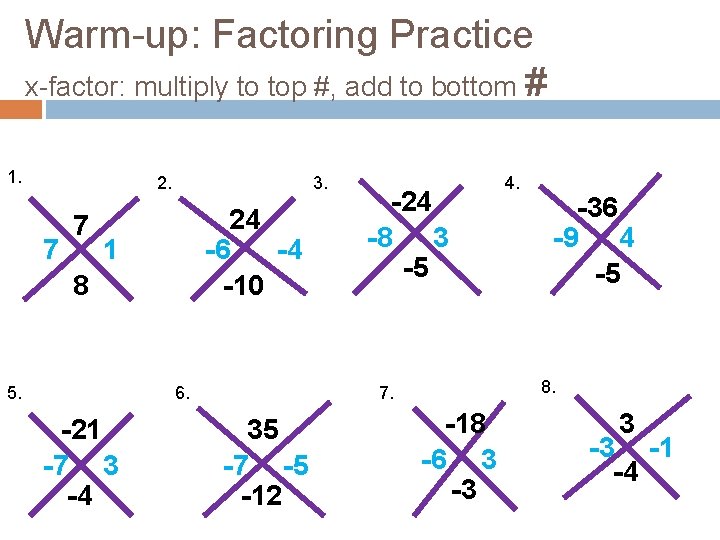
Warm-up: Factoring Practice x-factor: multiply to top #, add to bottom # 1. 2. 7 7 3. 24 -6 -4 -10 1 8 5. 6. -21 -7 3 -4 -24 -8 3 -5 -36 -9 4 -5 8. 7. 35 -7 -5 -12 4. -18 -6 3 -3 -1 -4

Factoring by Grouping Factor a common monomial, then look for a common binomial ? ? Do we remember monomials & binomials? ? ?

Factor out common binomial EX 1: 5 x 2(x – 2) – 3(x – 2) distributive property to factor (5 x 2 – 3)(x – 2) EX 2: 7 y(5 – y) + 3(y – 5) factor out -1 -7 y(y – 5) + 3(y – 5) distributive property to factor (-7 y + 3)(y – 5)

Factor by Grouping EX 3: m 3 + 7 m 2 – 2 m – 14 Group (m 3 + 7 m 2) + (-2 m – 14) Factor each group m 2(m + 7) + -2(m + 7) Distributive property (m 2 – 2)(m + 7)

Factor by Grouping EX 4: n 3 + 30 + 6 n 2 + 5 n Rearrange terms n 3 + 6 n 2 + 5 n + 30 Group terms (n 3 + 6 n 2) + (5 n + 30) Factor each group n 2(n + 6) + 5(n + 6) Distributive Property (n 2 + 5) (n + 6)

Factor Completely EX 5: 5 x 3 – 55 x 2 + 90 x Factor GCF 5 x(x 2 – 11 x + 18) Factor (x-factor) 5 x(x – 9)(x – 2) EX 6: 48 y 4 – 3 y 2 Factor GCF 3 y 2(16 y 2 – 1) Factor (special Product) 3 y 2(4 y – 1)(4 y + 1)

Solve a Polynomial Equation EX 7: 7 x 3 + 14 x 2 = 105 x Rearrange Equation 7 x 3 + 14 x 2 – 105 x = 0 Factor GCF 7 x(x 2 + 2 x – 15) = 0 Factor (x – factor) 7 x(x + 5)(x – 3) = 0 Zero Product Prop. 7 x = 0 x+5 = 0 x – 3 =0 x = -5 x=3

You Try…. 11 x(x-8) + 3(x-8) 4 x 3 – 36 x 32 y 10 x 3 + 21 y - 35 x 2 - 6 xy 9 x 3+9 x 2 – 7 x – 7 2 y 3 – 16 y 2 +