Factoring by Grouping ALGEBRA 1 LESSON 9 8

Factoring by Grouping ALGEBRA 1 LESSON 9 -8 (For help, go to Lessons 9 -2 and 9 -3. ) Find the GCF of the terms of each polynomial. 1. 6 y 2 + 12 y – 4 2. 9 r 3 + 15 r 2 + 21 r 3. 30 h 3 – 25 h 2 – 40 h 4. 16 m 3 – 12 m 2 – 36 m Find each product. 5. (v + 3)(v 2 + 5) 6. (2 q 2 – 4)(q – 5) 7. (2 t – 5)(3 t + 4) 8. (4 x – 1)(x 2 + 2 x + 3) Check Skills You’ll Need 9 -8

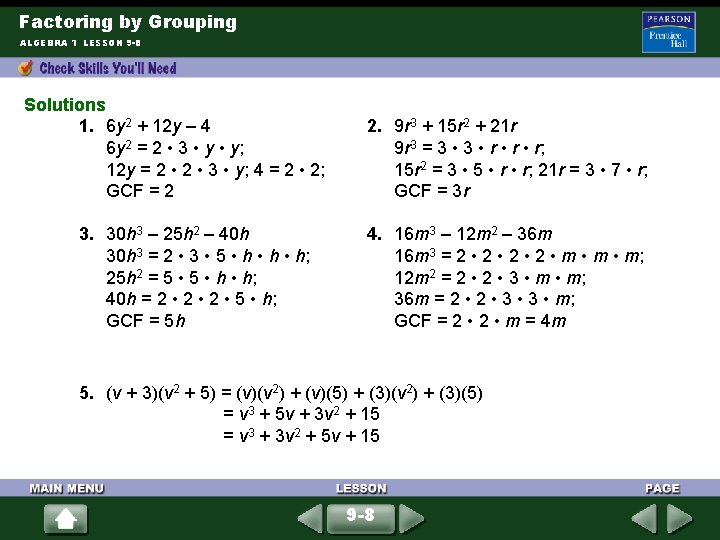
Factoring by Grouping ALGEBRA 1 LESSON 9 -8 Solutions 1. 6 y 2 + 12 y – 4 6 y 2 = 2 • 3 • y; 12 y = 2 • 3 • y; 4 = 2 • 2; GCF = 2 3. 30 h 3 – 25 h 2 – 40 h 3 = 2 • 3 • 5 • h • h; 25 h 2 = 5 • h • h; 40 h = 2 • 2 • 5 • h; GCF = 5 h 2. 9 r 3 + 15 r 2 + 21 r 9 r 3 = 3 • r • r; 15 r 2 = 3 • 5 • r; 21 r = 3 • 7 • r; GCF = 3 r 4. 16 m 3 – 12 m 2 – 36 m 16 m 3 = 2 • 2 • m • m; 12 m 2 = 2 • 3 • m; 36 m = 2 • 3 • m; GCF = 2 • m = 4 m 5. (v + 3)(v 2 + 5) = (v)(v 2) + (v)(5) + (3)(v 2) + (3)(5) = v 3 + 5 v + 3 v 2 + 15 = v 3 + 3 v 2 + 5 v + 15 9 -8

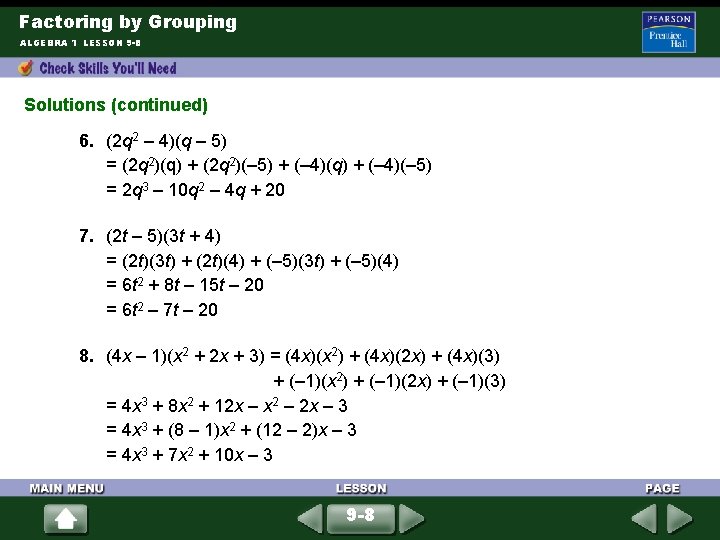
Factoring by Grouping ALGEBRA 1 LESSON 9 -8 Solutions (continued) 6. (2 q 2 – 4)(q – 5) = (2 q 2)(q) + (2 q 2)(– 5) + (– 4)(q) + (– 4)(– 5) = 2 q 3 – 10 q 2 – 4 q + 20 7. (2 t – 5)(3 t + 4) = (2 t)(3 t) + (2 t)(4) + (– 5)(3 t) + (– 5)(4) = 6 t 2 + 8 t – 15 t – 20 = 6 t 2 – 7 t – 20 8. (4 x – 1)(x 2 + 2 x + 3) = (4 x)(x 2) + (4 x)(2 x) + (4 x)(3) + (– 1)(x 2) + (– 1)(2 x) + (– 1)(3) = 4 x 3 + 8 x 2 + 12 x – x 2 – 2 x – 3 = 4 x 3 + (8 – 1)x 2 + (12 – 2)x – 3 = 4 x 3 + 7 x 2 + 10 x – 3 9 -8

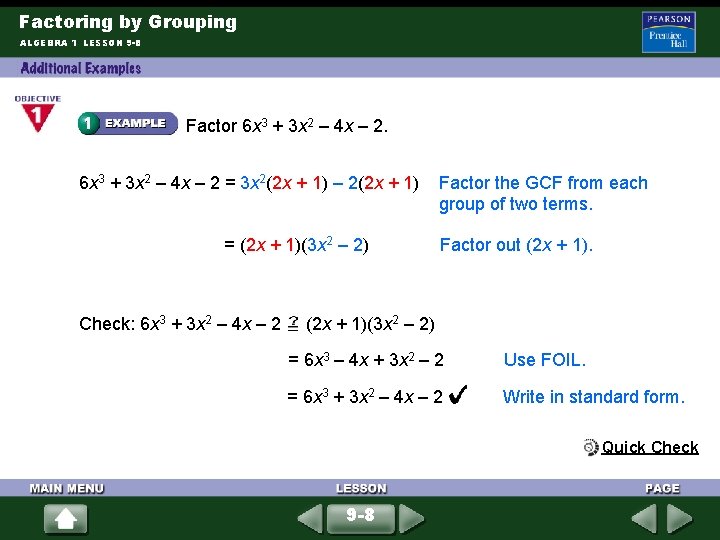
Factoring by Grouping ALGEBRA 1 LESSON 9 -8 Factor 6 x 3 + 3 x 2 – 4 x – 2 = 3 x 2(2 x + 1) – 2(2 x + 1) = (2 x + 1)(3 x 2 – 2) Check: 6 x 3 + 3 x 2 – 4 x – 2 Factor the GCF from each group of two terms. Factor out (2 x + 1)(3 x 2 – 2) = 6 x 3 – 4 x + 3 x 2 – 2 Use FOIL. = 6 x 3 + 3 x 2 – 4 x – 2 Write in standard form. Quick Check 9 -8

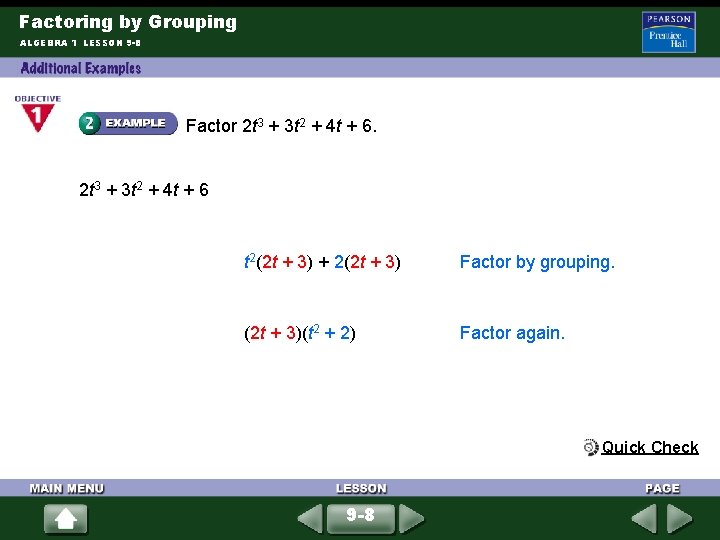
Factoring by Grouping ALGEBRA 1 LESSON 9 -8 Factor 2 t 3 + 3 t 2 + 4 t + 6 t 2(2 t + 3) + 2(2 t + 3) Factor by grouping. (2 t + 3)(t 2 + 2) Factor again. Quick Check 9 -8

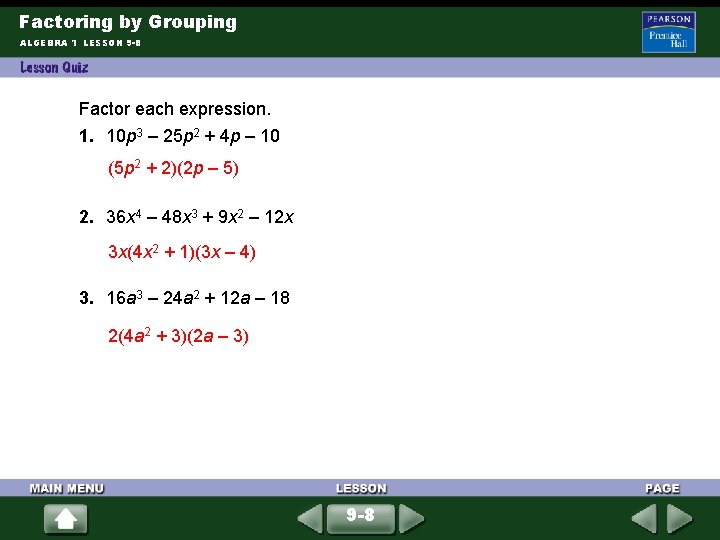
Factoring by Grouping ALGEBRA 1 LESSON 9 -8 Factor each expression. 1. 10 p 3 – 25 p 2 + 4 p – 10 (5 p 2 + 2)(2 p – 5) 2. 36 x 4 – 48 x 3 + 9 x 2 – 12 x 3 x(4 x 2 + 1)(3 x – 4) 3. 16 a 3 – 24 a 2 + 12 a – 18 2(4 a 2 + 3)(2 a – 3) 9 -8

Factoring to Solve Quadratic Equations ALGEBRA 1 Lesson 10 -4 Solve (2 x + 3)(x – 4) = 0 by using the Zero Product Property. (2 x + 3)(x – 4) = 0 2 x + 3 = 0 or x– 4=0 2 x = – 3 3 x=– 2 Use the Zero-Product Property. Solve for x. or x=4 3 Check: Substitute – 2 for x. Substitute 4 for x. (2 x + 3)(x – 4) = 0 [2(– 3 ) + 3](– 3 – 4) 2 2 (2 x + 3)(x – 4) = 0 0 [2(4) + 3](4 – 4) 1 0 (11)(0) = 0 (0)(– 5 2 ) = 0 10 -4 Quick Check

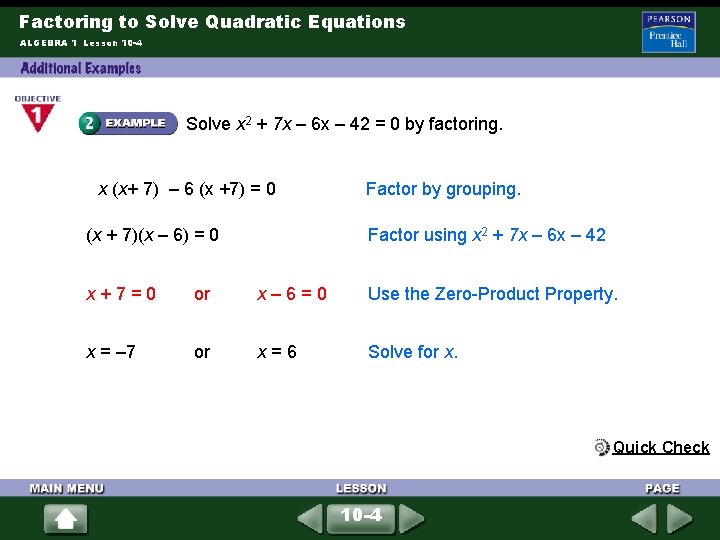
Factoring to Solve Quadratic Equations ALGEBRA 1 Lesson 10 -4 Solve x 2 + 7 x – 6 x – 42 = 0 by factoring. x (x+ 7) – 6 (x +7) = 0 (x + 7)(x – 6) = 0 Factor by grouping. Factor using x 2 + 7 x – 6 x – 42 x+7=0 or x– 6=0 Use the Zero-Product Property. x = – 7 or x=6 Solve for x. Quick Check 10 -4

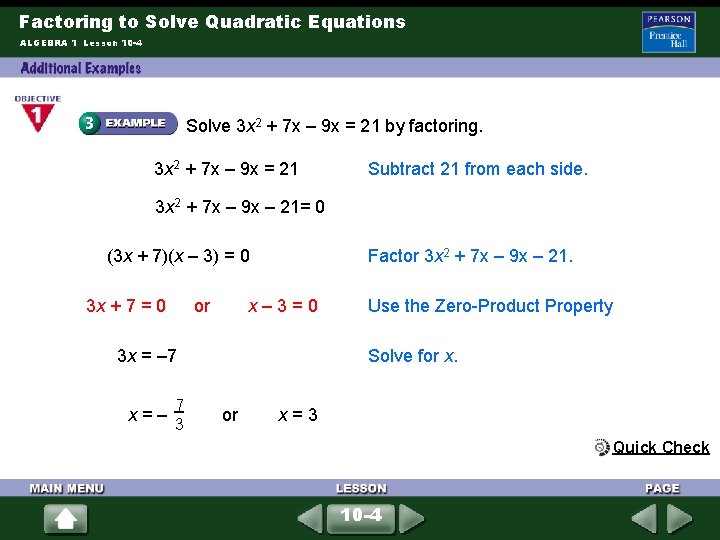
Factoring to Solve Quadratic Equations ALGEBRA 1 Lesson 10 -4 Solve 3 x 2 + 7 x – 9 x = 21 by factoring. 3 x 2 + 7 x – 9 x = 21 Subtract 21 from each side. 3 x 2 + 7 x – 9 x – 21= 0 (3 x + 7)(x – 3) = 0 3 x + 7 = 0 or Factor 3 x 2 + 7 x – 9 x – 21. x– 3=0 3 x = – 7 7 x=– 3 Use the Zero-Product Property Solve for x. or x=3 Quick Check 10 -4