Factor analysis and principal component analysis Chapter 10

Factor analysis and principal component analysis Chapter 10 Statistics for Marketing & Consumer Research Copyright © 2008 - Mario Mazzocchi 1

Data reduction methods • Useful to deal with large data-sets (many variables) and summarize information • The idea behind these methods is to avoid double counting of the same information by distinguishing between the individual information content of each variable and the amount of information shared across several variables • A data-set containing m correlated variables is condensed into a reduced set of p≤ m new variables (respectively factors or principal components according to the method used) that are uncorrelated between each other and explain a large proportion of the original variability Statistics for Marketing & Consumer Research Copyright © 2008 - Mario Mazzocchi 2

Pros and cons of data reduction • Data reduction is a necessary step to simplify data treatment when the number of variables is very large or when correlation between the original variables is regarded as an issue for subsequent analysis • The description of complex interrelations between the original variables is made easier by looking at the extracted factors (components), • The price is the loss of some of the original information and the introduction of an additional error component. Statistics for Marketing & Consumer Research Copyright © 2008 - Mario Mazzocchi 3

Factor and Principal Component Analysis • These are multivariate statistical methods designed to: • exploit the correlations between the original variables • create a smaller set of new artificial (or latent) variables that can be expressed as a combination of the original ones • The higher the correlation across the original variables, the smaller the number of artificial variables (factors or components) needed to adequately describe the phenomenon Statistics for Marketing & Consumer Research Copyright © 2008 - Mario Mazzocchi 4

History: the “g” factor • Many IQ tests, how many intelligences? • ‘G’ factor: general intelligence (common to all test) • ‘S’ factor: specific intelligence (specific to each test) • Or nine Intelligences: visual, perceptual, inductive, deductive, numerical, spatial, verbal, memory and word fluency Statistics for Marketing & Consumer Research Copyright © 2008 - Mario Mazzocchi 5

Examples of marketing applications • Data reduction – E. g. summarize the perceived value of a service/product starting from a multi-item questionnaire, for example the value of a bank service has been summarized into three dimensions: professional service, marketing efficiency and effective communication • Perceptual mapping, new market opportunities and product space – E. g. measure end-user’s preferences with respect to light dairy products and identify opportunities for new product development in lighter strawberry yoghurt as opposed to lighter Cheddar-type cheeses • Preliminary data preparation for market segmentation – E. g. market segmentation of computer gamers, three main drivers of gaming behaviour: attitudes (and knowledge), playing habits and buying habits. They eventually identify two types of gamers, hardcore and casual gamers Statistics for Marketing & Consumer Research Copyright © 2008 - Mario Mazzocchi 6

Factor analysis • A technique which is used for • the identification of latent variables and their relationship with a set of manifest indicators • data-reduction purposes, i. e. summarising a given set of variables into a reduced set of unrelated variables explaining most of the original variability Statistics for Marketing & Consumer Research Copyright © 2008 - Mario Mazzocchi 7

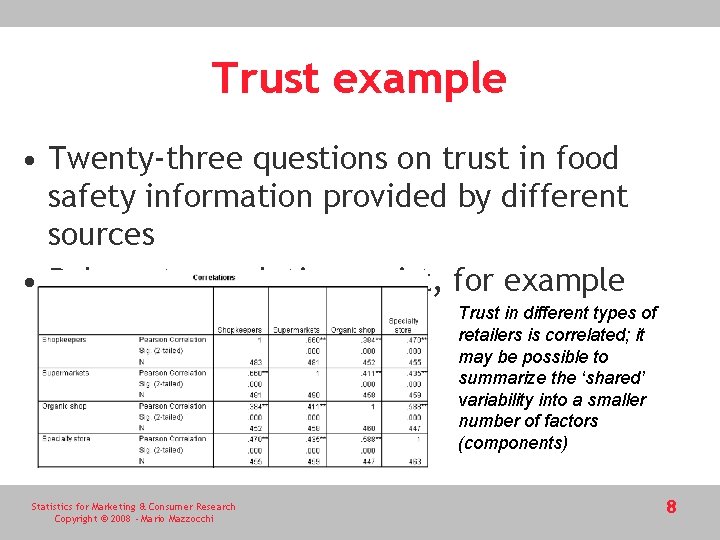
Trust example • Twenty-three questions on trust in food safety information provided by different sources • Relevant correlations exist, for example Trust in different types of retailers is correlated; it may be possible to summarize the ‘shared’ variability into a smaller number of factors (components) Statistics for Marketing & Consumer Research Copyright © 2008 - Mario Mazzocchi 8

Data reduction variability and correlation • In summary • For each of the original variables, only a certain amount of variability is specific to that variable • There is a fair amount of variability which is shared with other variables • Such shared variability can be fully summarized by the common factors • The method is potentially able to restructure into factors all of the original variability. This would be a rather useless exercise; the number of extracted factors should be equal to the number of original variables • The researcher faces a trade-off between the objective of reducing the dimension of the analysis and the amount of information lost by doing so. • These techniques are more effective and reliable when there are high levels of correlation across variables • When the links between the original variables are weak it will not be possible to perform a significant data reduction without losing a considerable amount of information Statistics for Marketing & Consumer Research Copyright © 2008 - Mario Mazzocchi 9

Factor Analysis(FA) and Principal Component Analysis(PCA) • A key difference between FA and PCA: – FA estimates p factors, where the number of factors p is lower than the number of variables n and needs to be assumed prior to estimation – One may compare results with different number of factors, for each of the analyses it is necessary to set preliminarily the number of factors p. – Instead, in PCA there is no need to run multiple analyses to choose the number of components – PCA starts by setting p=m, so that all of the variability is explained by the new factors (principal components). – The components are not estimated with error, but computed as the principal component problem and estimation method have an exact solution. – A reduced number of components can be selected at a later stage Statistics for Marketing & Consumer Research Copyright © 2008 - Mario Mazzocchi 10

Exploratory vs. Confirmatory Factor Analysis(CFA) • Exploratory factor analysis starts from observed data to identify unobservable and underlying factors, unknown to the researcher but expected to exist from theory (nine dimensions of intelligence? ) • CFA – the researcher wants to test one or more specific underlying structures, specified prior to the analysis. This is frequently the case in psychometric studies (see SEM, lecture 15) Statistics for Marketing & Consumer Research Copyright © 2008 - Mario Mazzocchi 11

Key concepts for factor analysis • What is summarised is the variability of the original data-set • There is no observed dependent variable as in regression, but interdependence (correlation) is explored • Each variable is explained by a set of underlying (non observed) factors • Each underlying factor is explained by the original set of variables • Hence. . . each variable is related to the remaining variables (interdependence) Statistics for Marketing & Consumer Research Copyright © 2008 - Mario Mazzocchi 12

Use of Factor Analysis 1. Estimation of the weights (factor loadings) that provide the most effective summarization of the original variability; 2. Interpretation of the sets of factor loadings to derive a meaningful label for each of the factors; 3. Estimation of the factor values (factor scores) so that these can be used in subsequent analysis in place of the original variables Statistics for Marketing & Consumer Research Copyright © 2008 - Mario Mazzocchi 13

Some notation p variables have been recorded on n individuals X is the data matrix xj indicates the generic variable j xij refers to the value of the j-th variable as recorded on the i-th individual X is the variance-covariance matrix of X Fk is the k-th underlying factor k: 1, 2, …, m m<p is the number of extracted factors (When m=p factor analysis becomes PCA) Statistics for Marketing & Consumer Research Copyright © 2008 - Mario Mazzocchi 14

Summarising interdependence – the covariance matrix • The original set of variables X is characterised by a p p variance-covariance matrix • The covariance matrix is a symmetric matrix, with the variance of the original variables on the diagonal and offdiagonal covariances Statistics for Marketing & Consumer Research Copyright © 2008 - Mario Mazzocchi 15

Factor analysis model The data matrix can be rewritten as a linear combination of the latent factors, plus an error term fi (i=1, 2, …, m) are uncorrelated random variables (common factors) m p mi (i=1, 2, …, p) are unique (specific) factors for each variable ei (i=1, 2, …, p) are error random variables, uncorrelated with each other and with F and represent the residual error due to the use of common factors Statistics for Marketing & Consumer Research 16 Copyright © 2008 - Mario Mazzocchi

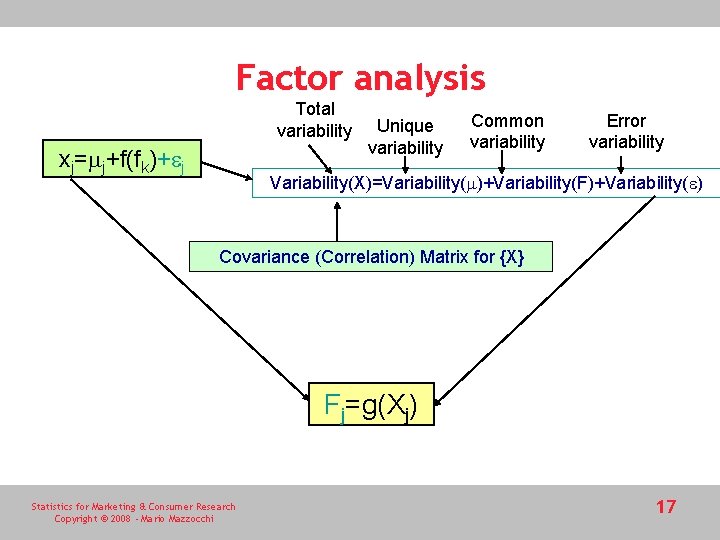
Factor analysis Total variability xj=mj+f(fk)+ej Unique variability Common variability Error variability Variability(X)=Variability(m)+Variability(F)+Variability(e) Covariance (Correlation) Matrix for {X} Fj=g(Xj) Statistics for Marketing & Consumer Research Copyright © 2008 - Mario Mazzocchi 17

The math of factor analysis X = m + GF + E This is the covariance matrix Assumption: Var(F)=I Statistics for Marketing & Consumer Research Copyright © 2008 - Mario Mazzocchi 18

Covariance matrix for the residual variable (error term) • By summarising the original data through m factors we commit an error measured by the residuals ei, whose diagonal variance-covariance matrix is Statistics for Marketing & Consumer Research Copyright © 2008 - Mario Mazzocchi 19

Terminology • An intuitive meaning can be attached to the factor coefficient matrix G (sometime referred to as the factor matrix). • Its elements g are called factor loadings and link the latent factor to the original variables, like correlations • is the communality of the i-th variable (the proportion of variance for each variable explained by the common factors) Statistics for Marketing & Consumer Research Copyright © 2008 - Mario Mazzocchi 20

Communalities • Relative communalities are between zero and one and tell us – for each variable – what percentage of the original variability is explained by the extracted factors Statistics for Marketing & Consumer Research Copyright © 2008 - Mario Mazzocchi 21

Estimation • Estimation in FA involves two objects: the factor loadings (and jointly the specific variances) and the factor scores • The two set of estimates cannot be obtained simultaneously and estimation of factor loadings always precedes estimation of factor scores. Statistics for Marketing & Consumer Research Copyright © 2008 - Mario Mazzocchi 22

FA model (factors view) f 1 = b 11 X 1+ b 12 X 2+… + b 1 p. Xp f 2 = b 21 X 1+ b 22 X 2+… + b 2 p. Xp fj = bj 1 X 1+ bj 2 X 2+… + bjp. Xp F = b. X fm = bp 1 X 1+ bp 2 X 2+… + bpp. Xp By inverting the FA equation, the common factors are expressed as linear combinations of the original variables Statistics for Marketing & Consumer Research Copyright © 2008 - Mario Mazzocchi 23

Steps in estimation Assuming a given number of factors: 1. 2. 3. 4. 5. Correlations among the original variables are exploited to obtain an initial guess for the factor loadings On the basis of this initial guess specific variances are estimated New estimates of the factor loadings are obtained according to some criterion (which varies according to the chosen method), conditional on estimates of the specific variances obtained in step 2 New estimates of the specific variances are obtained (again different methods can be used) conditional on estimates of the factor loadings obtained in step 3 Return to step (3) and proceed iteratively until estimates of factor loadings and specific variances are stable. Statistics for Marketing & Consumer Research Copyright © 2008 - Mario Mazzocchi 24

Estimation methods • Maximum likelihood: Estimates of factor loadings maximize a likelihood function conditional on the estimated sample covariance matrix. Multivariate normality is assumed for the data • Least-squares : Estimates are those that minimize the sum of the squared differences between the actual and estimated correlation matrices • Principal factoring: After the initial estimate on the specific variance (usually from regression analysis between the original variables), principal components are extracted from the difference between the sample covariance matrix and the estimated specific variances. New factor loadings and specific variances become available and the procedure is repeated iteratively • Alpha factoring: An initial principal component analysis is followed by estimation of the factor loadings through a criterion which maximizes the Cronbach alpha-reliability index • Image factoring: Each of the original variables is regressed on the remaining ones and the model is used to obtain within-sample predictions. These predictions (images) allow one to compute the specific and residual variances Statistics for Marketing & Consumer Research Copyright © 2008 - Mario Mazzocchi 25

Estimation methods characteristics • principal factoring and image factoring are not independent from the measurement scales of the original variables. • In fact, one may choose to apply them either to the correlation or to the covariance matrix of the original data. • Using the correlation matrix corresponds to standardizing the original variables and eliminates the effects of different measurement units or scales, but it also implies that all the original variables have the same variability (not always desirable) • If the measurement scale and unit are the same across variables, there is no reason to force variability to be equal across variables ( better to use the covariance matrix and maintain the measurement scales) • The other methods, and maximum likelihood should be preferred, are independent from such choices. • Compare maximum likelihood results with those from principal (image) factoring to assess the influence of the scale of measurement Statistics for Marketing & Consumer Research Copyright © 2008 - Mario Mazzocchi 26

Estimation of factor scores • Regression: If multivariate normality is assumed for the factors and for the specific component, express the factor scores as a function of the observed data (in this way they can be seen as regression predictions). Drawback – the estimated factor may be correlated (contrarily to assumptions). • Bartlett scores: This method considers the FA equation as a system of regression equations where the original variables are the dependent variables, the factor loadings are the explanatory variables and the factor scores are the unknown parameters. Estimation of the scores is obtained by weighted least squares to account for heteroskedasticity. Again, estimated factor scores may be correlated • Anderson-Rubin: The appropriate method when theoretical factors are uncorrelated and produces perfectly uncorrelated estimates. Statistics for Marketing & Consumer Research Copyright © 2008 - Mario Mazzocchi 27

Choice of the number of factors • Under extraction (less factors than in the underlying structure) or over extraction (too many factors) produce a bias on the results. • Over extraction is less serious than under extraction – better to risk an excess of factors than the opposite • The choice of the number of factors can be based on ad hoc techniques (e. g. scree diagram) • With maximum likelihood methods, the likelihood ratio provides a test for the initial assumption on the number of factors or as a benchmark for comparison with different initial choices (assumption – normally distributed data) • Akaike Information Criterion (AIC) – the factor structure which best fits the data corresponds to the lowest AIC value. • When the number of factors is uncertain run the factor analysis for different numbers of factors and compare the solutions according to goodness-of-fit statistics. Statistics for Marketing & Consumer Research Copyright © 2008 - Mario Mazzocchi 28

Bartlett’s tests • The Bartlett’s test of sphericity can be computed when multivariate normality of the original variables can be safely assumed and the maximum likelihood estimation method is applied • The test is applied to the correlation matrix. The null hypothesis is that the original correlation matrix is equal to an identity matrix. If not rejected there are no grounds for searching common factors. • A second test named after Bartlett is a corrected likelihood ratio test not to be confused with the sphericity test. • It tests whether the selected number of factors explains a significant portion of the original variability (but it is sensitive to sample size) Statistics for Marketing & Consumer Research Copyright © 2008 - Mario Mazzocchi 29

Interpretation of factors • Interpretation is based on the value of the factor loadings for each factor. • The factor loadings are the correlations between each of the original variables and the factor and are bounded between minus one and plus one, where high (positive or negative) value indicate that the link between the factor and the considered variable is very strong. • Statistical significance of the factor loadings. Complication: the standard errors are usually so high that few variables emerge as relevant in explaining a factor. • The statistical relevance of a factor loading depends on its absolute value and the sample size, so that the same value for a factor loading assumes different relevance depending on the sample size. Rule of thumb: with a sample of 100 units a reasonable threshold is 0. 55 while with 200 units the value falls to 0. 40 and with 50 units it rises to 0. 75. Statistics for Marketing & Consumer Research Copyright © 2008 - Mario Mazzocchi 30

Factor rotation • • Factor loadings are not unique Indeterminacy problem Rotation may improve interpretability Estimation methods guarantee optimality according to some mathematical rule but not optimality with respect to interpretability • Trade-off Statistics for Marketing & Consumer Research Copyright © 2008 - Mario Mazzocchi 31

Rotating or not? • Philosophical grounds of the analysis • If it is assumed that the latent factor exist but cannot be directly measured, then meaningfulness of the results is a priority. • If the objective is only data reduction, regardless of the factor meaning, there is no need for rotation Statistics for Marketing & Consumer Research Copyright © 2008 - Mario Mazzocchi 32

Rotation methods • Rotation methods can be classified in orthogonal rotation methods and oblique rotation methods. • Orthogonal methods assume that the factor remain uncorrelated. In some circumstances, the researchers may want to relax such an assumption to make interpretation even easier. • Oblique rotation methods allow for correlated factors. There are major implications in using oblique rotation methods. Although they can lead to further simplification of the factor matrix, it becomes less straightforward to evaluate the contribution of each factor in explaining the original variability. Statistics for Marketing & Consumer Research Copyright © 2008 - Mario Mazzocchi 33

Orthogonal rotation methods • Varimax: Maximizes variance of loadings on each factor (column of the factor matrix). Each factor is explained by few variables (but possibly the same variables can be relevant to explain two or more factors). • Quartimax: Maximizes variance of loadings on each variable (row of the factor matrix). Each variable is expected to explain a reduced number of factors (but one factor may need to be interpreted by a large number of variables) • Equamax: A compromise which is equidistant between Varimax and Quartimax • Orthomax: As for Equamax, a compromise between Varimax and Quartimax, where the researcher decides the relative weight of the Varimax component versus the Quartimax one. • Parsimax: Specific case of Orthomax rotation where the relative weights of the Varimax and Quartimax rotations depends on the number of variables and factors. Statistics for Marketing & Consumer Research Copyright © 2008 - Mario Mazzocchi 34

Oblique rotation methods • Orthoblique: a Quartimax (orthogonal) rotation is applied to the rescaled factor loadings so that the original non-scaled factors might be correlated. • Procrustres: The researcher sets a target factor matrix and the rotation matrix is the one which best approximates the target solution. This rotation can be seen as a test of the hypothesized factor loadings. • Promax: Starting from an orthogonal solution, further oblique rotation aims to drive to zero those factor loadings that are smaller. This is achieved by raising to powers the orthogonal loadings. Statistics for Marketing & Consumer Research Copyright © 2008 - Mario Mazzocchi 35

PCA and FA • In SPSS, PCA is treated as a special case(estimation method) of FA. • The PCA factors are built in a way that the amount of original variance explained by the first component is the highest and progressively decreases through the subsequent components • Principal components consider and replicate all of the original variability, whereas in FA estimates are based only on common variance • All original variance is considered, whereas in FA the estimates are only based on common variance • Component scores can be computed exactly whilst factor scores are estimated. There is no guarantee that estimated factor scores will actually be uncorrelated between each other Statistics for Marketing & Consumer Research Copyright © 2008 - Mario Mazzocchi 36

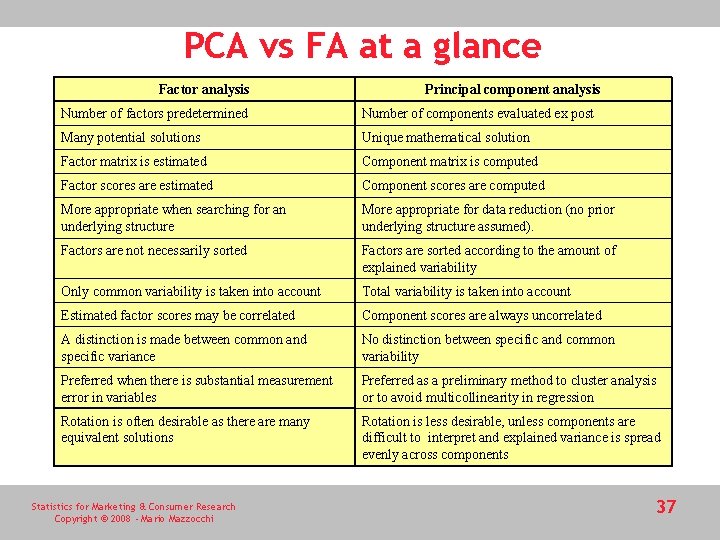
PCA vs FA at a glance Factor analysis Principal component analysis Number of factors predetermined Number of components evaluated ex post Many potential solutions Unique mathematical solution Factor matrix is estimated Component matrix is computed Factor scores are estimated Component scores are computed More appropriate when searching for an underlying structure More appropriate for data reduction (no prior underlying structure assumed). Factors are not necessarily sorted Factors are sorted according to the amount of explained variability Only common variability is taken into account Total variability is taken into account Estimated factor scores may be correlated Component scores are always uncorrelated A distinction is made between common and specific variance No distinction between specific and common variability Preferred when there is substantial measurement error in variables Preferred as a preliminary method to cluster analysis or to avoid multicollinearity in regression Rotation is often desirable as there are many equivalent solutions Rotation is less desirable, unless components are difficult to interpret and explained variance is spread evenly across components Statistics for Marketing & Consumer Research Copyright © 2008 - Mario Mazzocchi 37

Principal Component Analysis No error term, p components is a n p matrix of principal component scores, with p columns (one for each principal component cj) and n rows (one for each statistical unit) X is the usual n p data matrix component loadings Statistics for Marketing & Consumer Research Copyright © 2008 - Mario Mazzocchi is the p p matrix of 38

Two further constraints • The component scores are uncorrelated across components or which corresponds to the condition • The coefficients size across components must be constrained, otherwise the variances of the principal components would depend on the coefficients sizes as well while the aim is that they are only determined by the different weight of the original variables. Statistics for Marketing & Consumer Research Copyright © 2008 - Mario Mazzocchi 39

The PCA equation • PCA consists in finding the aj vectors that maximize the right-hand side of the above equation, subject to the specified constraints on C and A • It starts from the first component (the one with the largest variance) and proceeds until the last (the one with the smallest variance) • The total variability of the p extracted components equals the total variability of the p original variables; the first step of PCA simply consists in passing from a set of p variables (X) to an alternative set of p variables (the principal components in C), • Principal componentsa re • • linear combinations of the original variables uncorrelated between each other. • One may then decide to select a sub-set of components. • The vectors aj are the latent vectors (characteristic vectors or eigenvectors) of the covariance matrix , while the values lj. are the corresponding latent roots (characteristic roots or eigenvalues). • The eigenvectors and eigenvalues are unique and can be computed algebraically. Statistics for Marketing & Consumer Research Copyright © 2008 - Mario Mazzocchi 40

Component scores • The eigenvalues can be used as a criterion to decide the number of components to be retained for data summarization and subsequent analyses. • Once the matrix A has been computed, the component scores can be also (exactly) computed by simply applying • It may be convenient to standardize the component scores so that they all have variance equal to one. In this case, the coefficient score aij is rescaled • SPSS automatically provides standardized component scores; to maintain the original component variability and the correct balance among components the inverse operation is needed Statistics for Marketing & Consumer Research Copyright © 2008 - Mario Mazzocchi 41

Correlation vs. Covariance • PCA can be applied on either the correlation or covariance matrix – with different results. Which way to go? 1) When the measurement unit is the same for all variables, the covariance matrix should be used 2) When the measurement unit differs across variables andor it is desirable that all variables have the same weight on the analysis, regardless of their variability, the correlation matrix should be used 3) When the measurement unit differs across variables and the researcher wants to take into account the original variability, a solution might be a re-scaling of the original variables • The resulting variables are now expressed as indices with respect to their mean values but maintain the ranges of the original variables. PCA can be applied to their covariance matrix Statistics for Marketing & Consumer Research Copyright © 2008 - Mario Mazzocchi 42

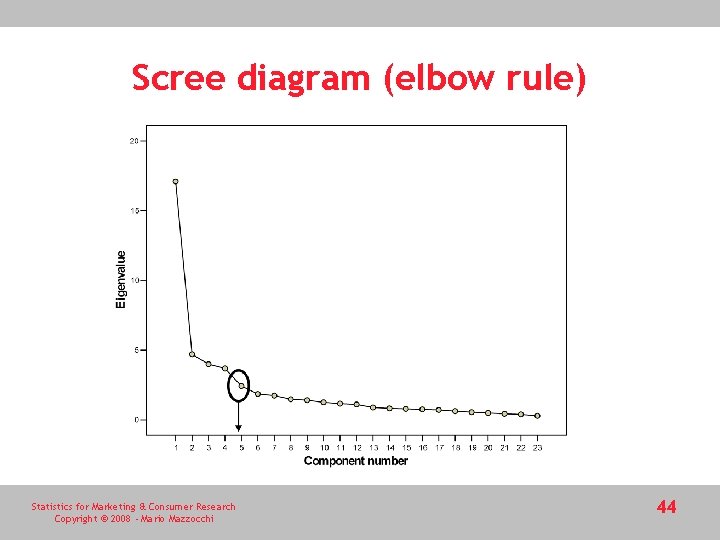
Choice of the number of principal components • Level of explained variance • • Usually the first m components explaining 70%-80% of the total variability Eigenvalues of the data correlation matrix The eigenvalues corresponding to each component represent the amount of variance they explain. The sum of eigenvalues equals the original number of variables • Eigenvalues larger than one (explaining more variance than the average component) • Scree diagram Statistics for Marketing & Consumer Research Copyright © 2008 - Mario Mazzocchi 43

Scree diagram (elbow rule) Statistics for Marketing & Consumer Research Copyright © 2008 - Mario Mazzocchi 44

Communalities • where the li are the eigenvalues and aij are the elements of the eigenvectors as before • The first term on the right-hand side of the equation represents the amount of variance which is summarized by the retained components, while the second term is the amount of variance discarded by selecting only the first k components. • The communality for each variable is then computed as: Statistics for Marketing & Consumer Research Copyright © 2008 - Mario Mazzocchi 45

Rotation • As for factor analysis component can be also orthogonally or obliquely rotated but there are differences and drawbacks to be taken into account • Rotation should concern all of the components and not only the selected one because • Otherwise there is no guarantee that the k selected components are still those which explain the larger amount of variability • Disparities in explained variability after rotation are generally smaller than before • Rotation is less problematic when explained variability is already evenly spread at the extraction of principal components. • There are many rotation methods for principal components; those discussed for factor analysis can be also applied to PCA. Statistics for Marketing & Consumer Research Copyright © 2008 - Mario Mazzocchi 46

SPSS – Trust example Factor Analysis 1. Explore the correlation matrix for the original data matrix 2. Perform factor analysis and estimate factor loadings by maximum likelihood 3. Choose the number of factors 4. Examine the factor matrix 5. Rotate the factor matrix to improve readability 6. Estimate factor scores Statistics for Marketing & Consumer Research Copyright © 2008 - Mario Mazzocchi 47

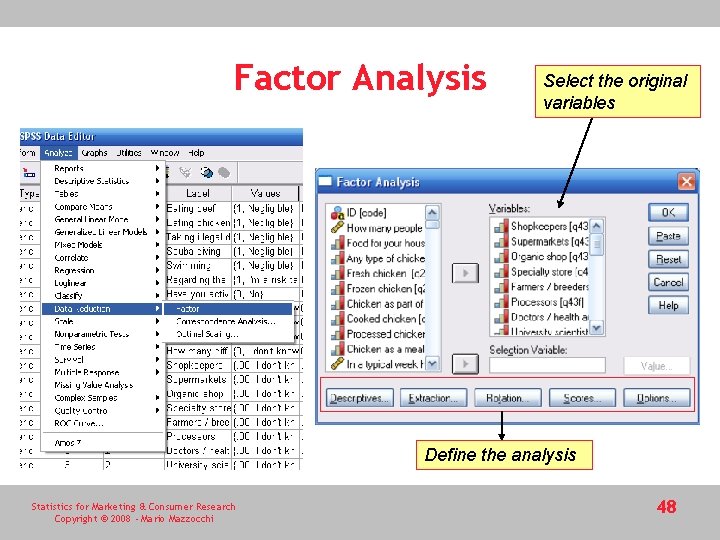
Factor Analysis Select the original variables Define the analysis Statistics for Marketing & Consumer Research Copyright © 2008 - Mario Mazzocchi 48

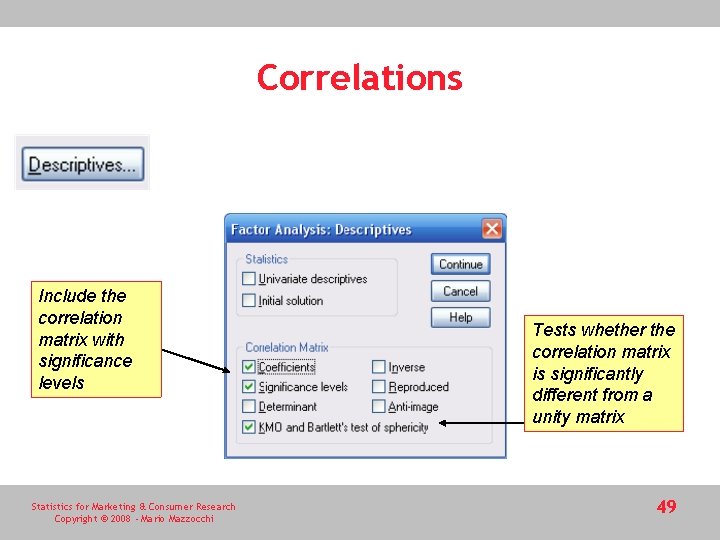
Correlations Include the correlation matrix with significance levels Statistics for Marketing & Consumer Research Copyright © 2008 - Mario Mazzocchi Tests whether the correlation matrix is significantly different from a unity matrix 49

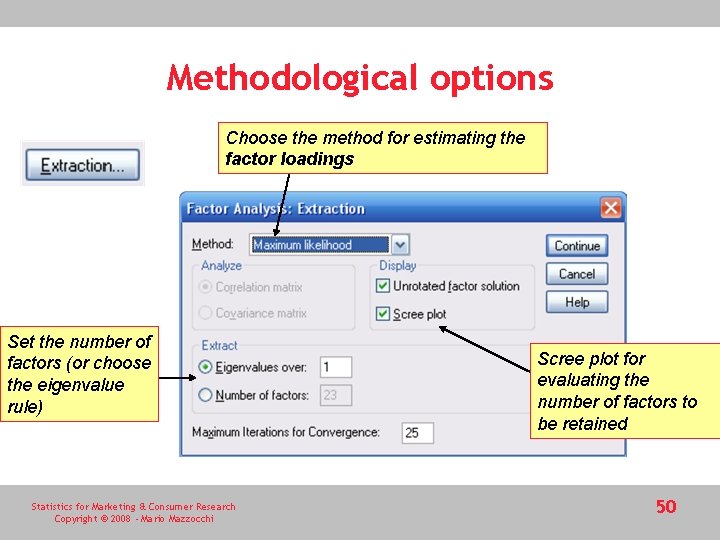
Methodological options Choose the method for estimating the factor loadings Set the number of factors (or choose the eigenvalue rule) Statistics for Marketing & Consumer Research Copyright © 2008 - Mario Mazzocchi Scree plot for evaluating the number of factors to be retained 50

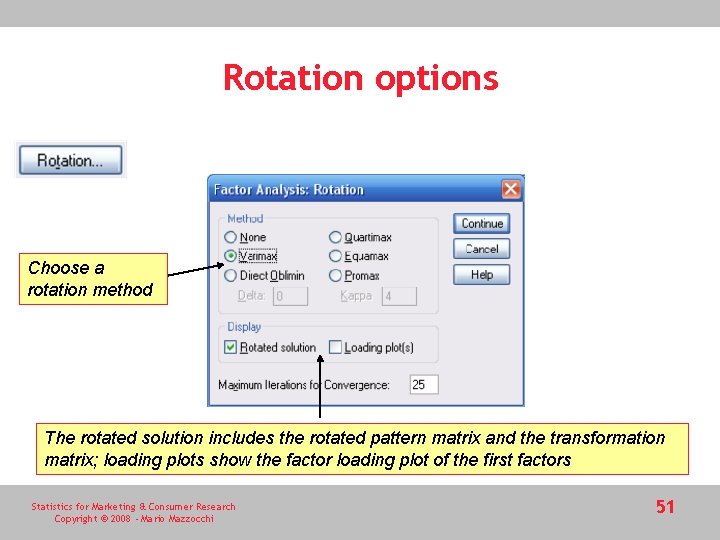
Rotation options Choose a rotation method The rotated solution includes the rotated pattern matrix and the transformation matrix; loading plots show the factor loading plot of the first factors Statistics for Marketing & Consumer Research Copyright © 2008 - Mario Mazzocchi 51

Estimation of factor scores Tick here to create new variables containing the estimated factor scores for each case in the dataset Choose the method for estimating the factor scores Show the coefficients of the factor score estimating equation Statistics for Marketing & Consumer Research Copyright © 2008 - Mario Mazzocchi 52

Other options Indicate how to deal with missing values Improve readability of the factor matrix by suppressing small coefficients (see earlier discussion on significance of factor loadings) Statistics for Marketing & Consumer Research Copyright © 2008 - Mario Mazzocchi 53

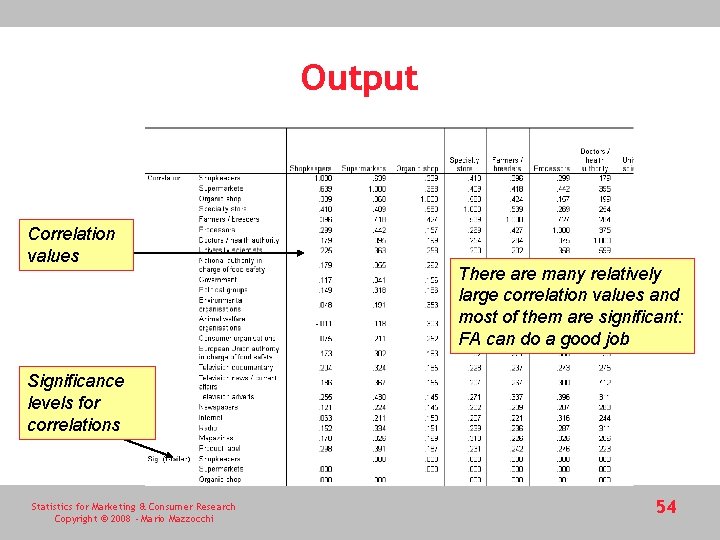
Output Correlation values There are many relatively large correlation values and most of them are significant: FA can do a good job Significance levels for correlations Statistics for Marketing & Consumer Research Copyright © 2008 - Mario Mazzocchi 54

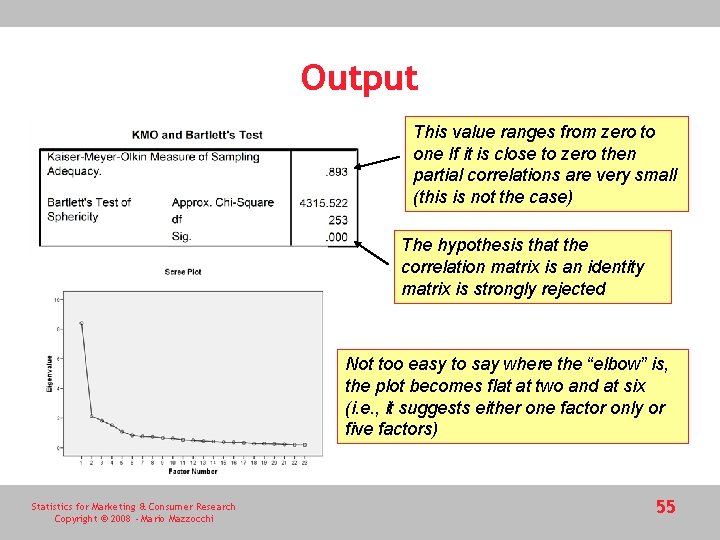
Output This value ranges from zero to one If it is close to zero then partial correlations are very small (this is not the case) The hypothesis that the correlation matrix is an identity matrix is strongly rejected Not too easy to say where the “elbow” is, the plot becomes flat at two and at six (i. e. , it suggests either one factor only or five factors) Statistics for Marketing & Consumer Research Copyright © 2008 - Mario Mazzocchi 55

Output This is the factor matrix (the unrotated factor loadings) Five factors have been extracted (based on the eigenvalue>1 rule) The loadings explain the relationship (like correlation) between the original variables and the extracted factor – so that they may be interpreted and labelled • Almost all variables load into the first factor (general trust) • The second factor has a + loading for radio and a – loading on the national authority (definition not easy) • The third factor emphasizes trust towards common retailers… and so on Statistics for Marketing & Consumer Research Copyright © 2008 - Mario Mazzocchi 56

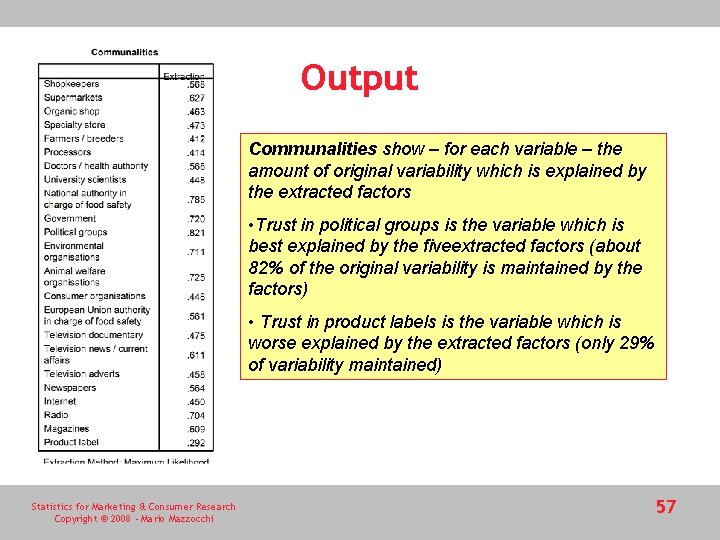
Output Communalities show – for each variable – the amount of original variability which is explained by the extracted factors • Trust in political groups is the variable which is best explained by the fiveextracted factors (about 82% of the original variability is maintained by the factors) • Trust in product labels is the variable which is worse explained by the extracted factors (only 29% of variability maintained) Statistics for Marketing & Consumer Research Copyright © 2008 - Mario Mazzocchi 57

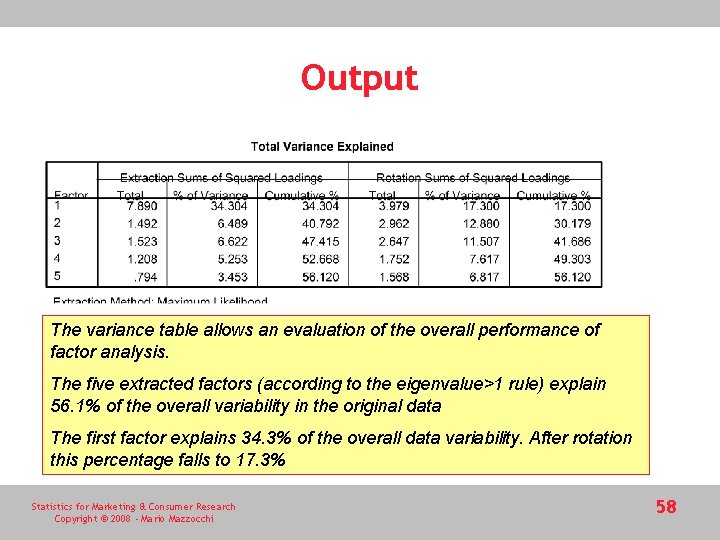
Output The variance table allows an evaluation of the overall performance of factor analysis. The five extracted factors (according to the eigenvalue>1 rule) explain 56. 1% of the overall variability in the original data The first factor explains 34. 3% of the overall data variability. After rotation this percentage falls to 17. 3% Statistics for Marketing & Consumer Research Copyright © 2008 - Mario Mazzocchi 58

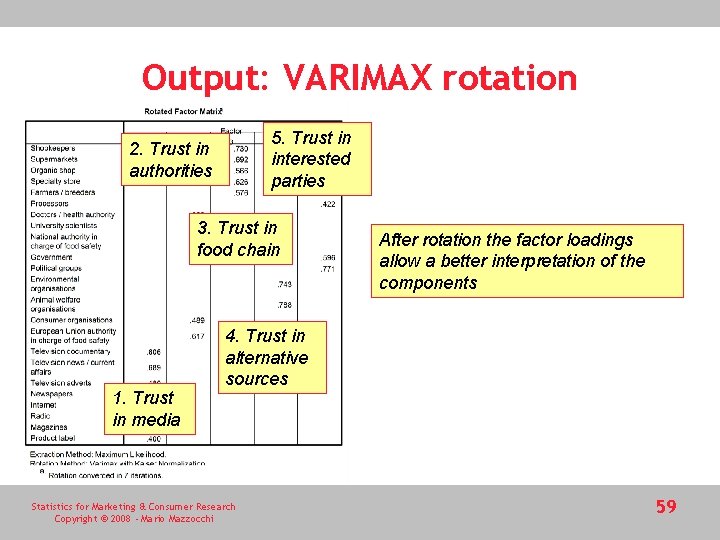
Output: VARIMAX rotation 5. Trust in interested parties 2. Trust in authorities 3. Trust in food chain 1. Trust in media After rotation the factor loadings allow a better interpretation of the components 4. Trust in alternative sources Statistics for Marketing & Consumer Research Copyright © 2008 - Mario Mazzocchi 59

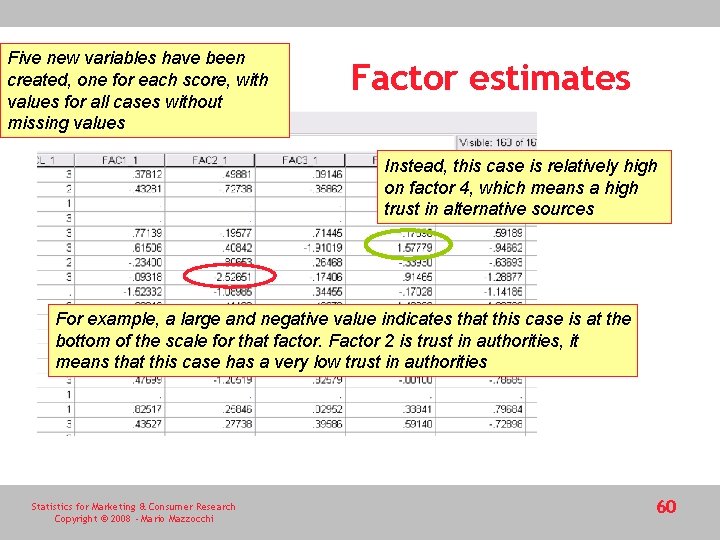
Five new variables have been created, one for each score, with values for all cases without missing values Factor estimates Instead, this case is relatively high on factor 4, which means a high trust in alternative sources For example, a large and negative value indicates that this case is at the bottom of the scale for that factor. Factor 2 is trust in authorities, it means that this case has a very low trust in authorities Statistics for Marketing & Consumer Research Copyright © 2008 - Mario Mazzocchi 60

Factor estimates • Is it true? Let us see how this synthesis works • Case 8 – Low trust in authorities (-2. 5 in factor 2): Minimum trust (1) for government and European Authority, very low trust (2) for government, national authority and health authorities • Case 6 – High trust in alternative sources (+1. 58 in factor 4): maximum trust (7) for both environmental organization and animal welfare organizations Statistics for Marketing & Consumer Research Copyright © 2008 - Mario Mazzocchi 61

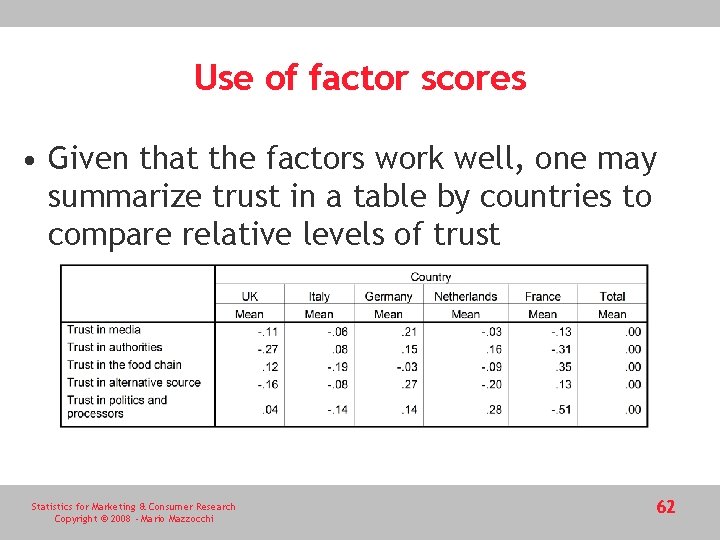
Use of factor scores • Given that the factors work well, one may summarize trust in a table by countries to compare relative levels of trust Statistics for Marketing & Consumer Research Copyright © 2008 - Mario Mazzocchi 62

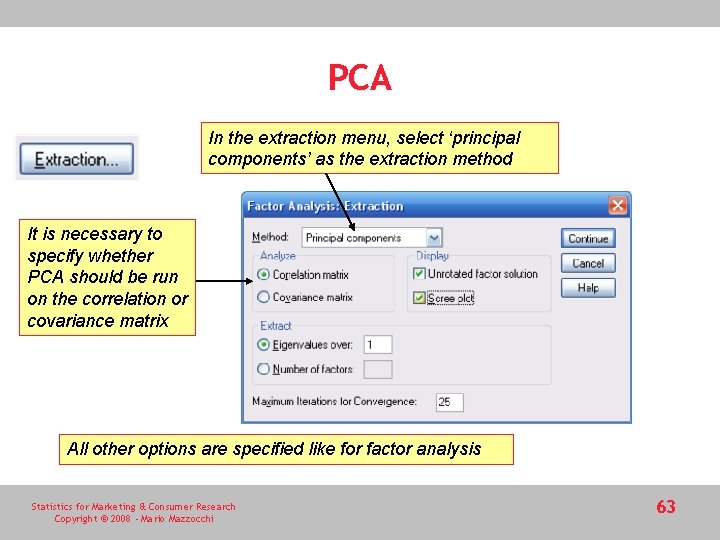
PCA In the extraction menu, select ‘principal components’ as the extraction method It is necessary to specify whether PCA should be run on the correlation or covariance matrix All other options are specified like for factor analysis Statistics for Marketing & Consumer Research Copyright © 2008 - Mario Mazzocchi 63

Communalities As an initial step, a number of components equal to the number of variables is extracted. This means that all of the original variability is explained by the components and communalities are all equal to one Statistics for Marketing & Consumer Research Copyright © 2008 - Mario Mazzocchi These are the communalities after the number of selected components has been fixed (e. g. according to the eigenvalue>1 rule) 64

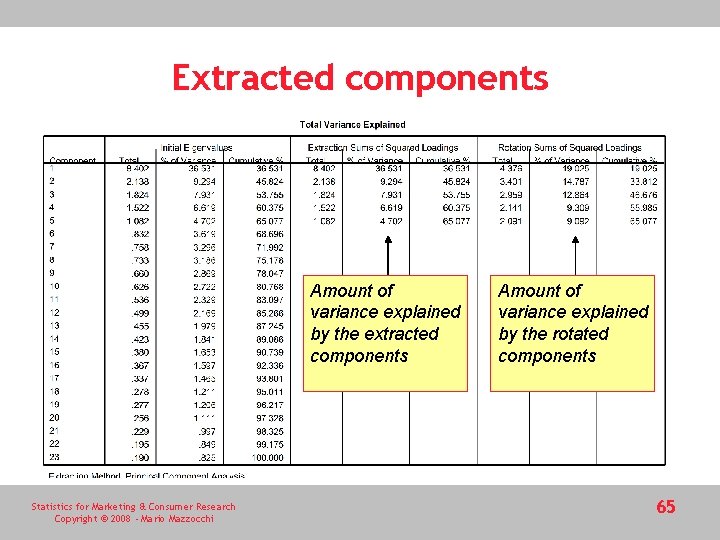
Extracted components Amount of variance explained by the extracted components Statistics for Marketing & Consumer Research Copyright © 2008 - Mario Mazzocchi Amount of variance explained by the rotated components 65

Component matrix These are the component loadings before rotation Statistics for Marketing & Consumer Research Copyright © 2008 - Mario Mazzocchi 66

Rotated component matrix The rotated component matrix shares many similarities with factor analysis (which suggest that the solution is robust) Statistics for Marketing & Consumer Research Copyright © 2008 - Mario Mazzocchi 67

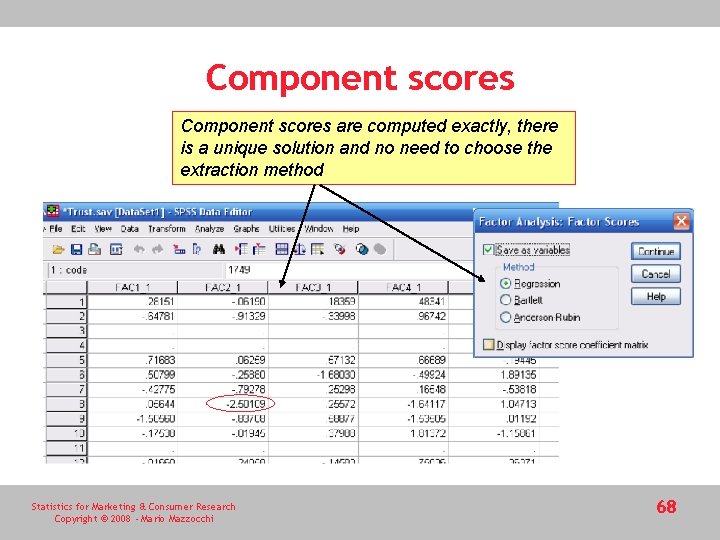
Component scores are computed exactly, there is a unique solution and no need to choose the extraction method Statistics for Marketing & Consumer Research Copyright © 2008 - Mario Mazzocchi 68