FACIAL RECONSTRUCTION AND RECOGNITION USING LINEAR ALGEBRA ANDREW

FACIAL RECONSTRUCTION AND RECOGNITION USING LINEAR ALGEBRA ANDREW ZUCKER ●● MATH 2860 RESEARCH PROJECT

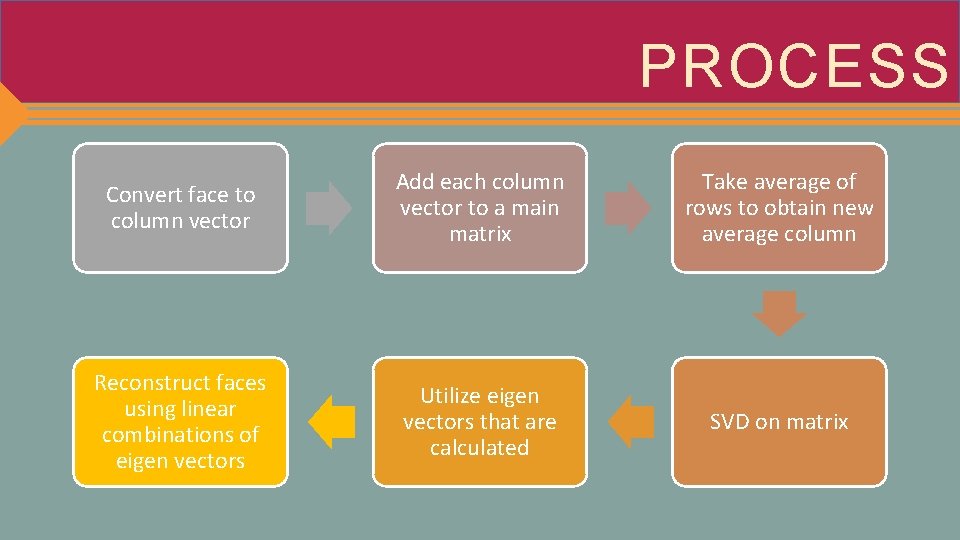
PROCESS Convert face to column vector Add each column vector to a main matrix Take average of rows to obtain new average column Reconstruct faces using linear combinations of eigen vectors Utilize eigen vectors that are calculated SVD on matrix

CREATING A FACE DATABASE n 1. Use a uniform naming system TRAINING SET … 2 3 n m m m 2 … m x m matrix m 2 x n matrix 1 2. Ensure all dimensions are uniform 3. Convert images to a column vector 4. Place each column vector into a larger, main matrix

CALCULATE AVERAGE FACE COLUMN MATRIX m 2 • Take arithmetic average of the rows to get a single column vector • This new column vector is the average face • Subtract from every face column vector • This takes out all of the common features between faces

S. V. D. • Singular variable decomposition is a tool used to simplify a matrix • It has three components, U, Σ, and V* • Σ represents the singular values • U represents the left singular values • V* represents the right singular values • M represents the original matrix U Σ V* = M

S. V. D. • The U vector is a set of eigenvectors of M and V* is another • This technique extracts unique features that can be seen as “eigenfaces” • The images on the right are columns of U and represent the directions of greatest differences U • A property of SVD is the order that the columns are in, they are sorted from greatest to least difference • Faces get “noisier” as you progress to the right Eigenvectors converted back to images

REPRESENTING FACES • F represents a face column vector • The dot product of U and F gives a scalar coefficient Reconstruction approximation of the given face Original Face • This can be visualized as a scalar combination of the eigen vectors to create a face + Average Face W = U * F W 1* + W 2* + W 3* +Wn*

REPRESENTING FACES • The program is doing its best to replicate the given face by using the faces it already knows (the training set) Reconstruction • From here, the framework for facial recognition has been laid Original Face out + Average Face W = U * F W 1* + W 2* + W 3* +W 4* There will likely be more than four eigenvectors

TESTING AN UNKNOWN FACE • This is an attempt at reconstructing an untrained face. • The training set is 200 faces, not all of which are unique Test Subject: Al Gore Left: What machine ‘sees’ Right: Original • Somewhere in the program, the face gets mirrored, this is a bug picture • For testing my face, I tried with 200 in the training set, and it came out looking bad, so I doubled the set and got this result to the right Test Subject: “Dubya” Left: What machine ‘sees’ Right: Original picture Test Subject: Me Left: What machine ‘sees’ Right: Original picture (Training set of 400 faces, not including mine)

MATCHING FACES • Repeat this dot product for an unidentified face • The weight vector is then compared to all of the calculated weight vectors within the training set • The comparison is done as a difference of distance within the weight vector’s space • If the distance is below a certain threshold, a match is assumed W = U * F