f Problem Obtain intensity formula by integration Intensity

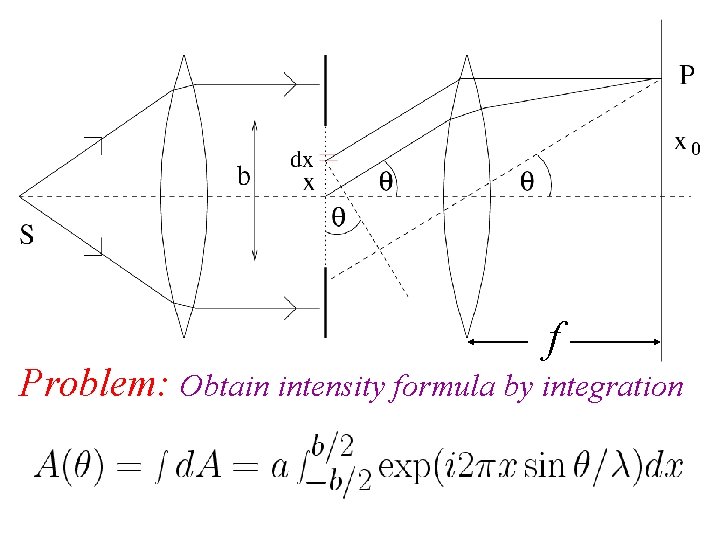
f Problem: Obtain intensity formula by integration

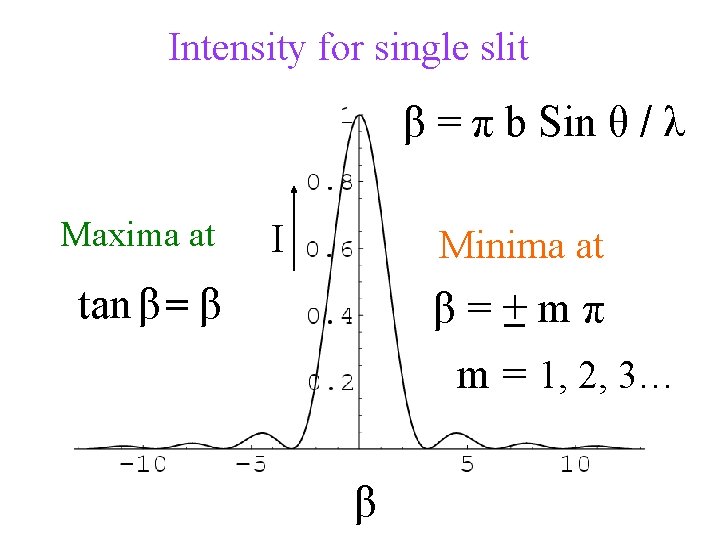
Intensity for single slit β = π b Sin θ / λ Maxima at I Minima at β = +_ m π tan β = β m = 1, 2, 3… β

For Principal maxima

For minima

For extrema of I(q) tan β = β

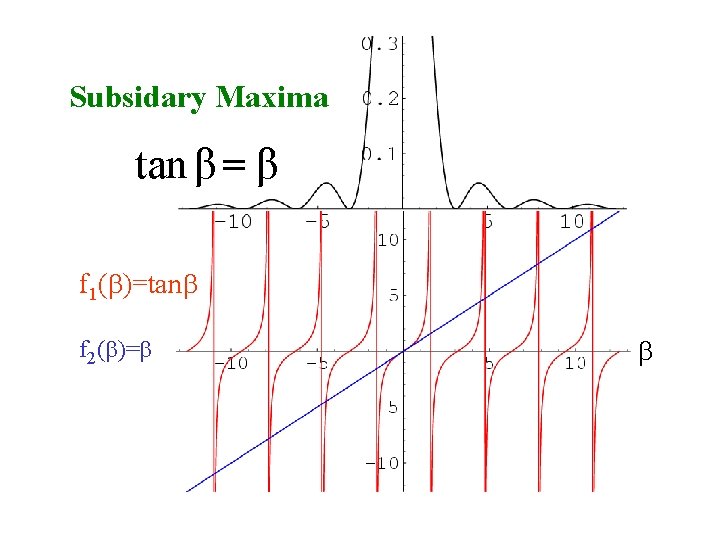
Subsidary Maxima tan β = β f 1(b)=tanb f 2(b)=b b

For subsidiary maxima

Half width of central maximum =λ/b Diffraction envelope size Δ x 0 = f λ / b Δ x 0 Point source Smearing effect of diffraction

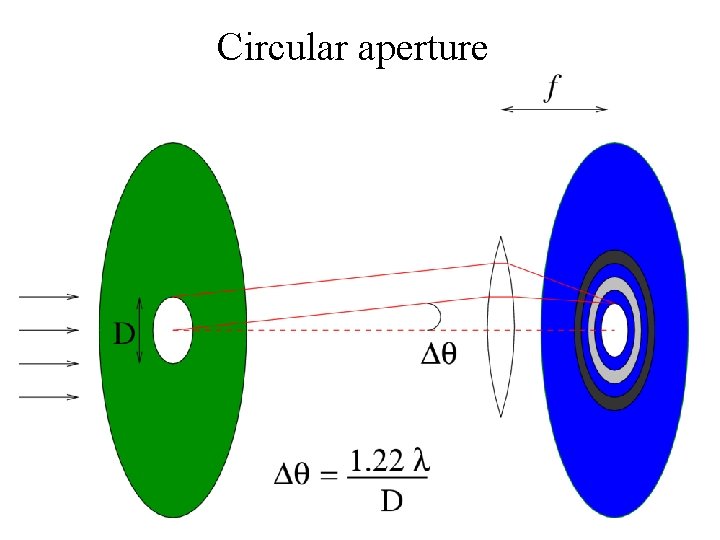
Circular aperture

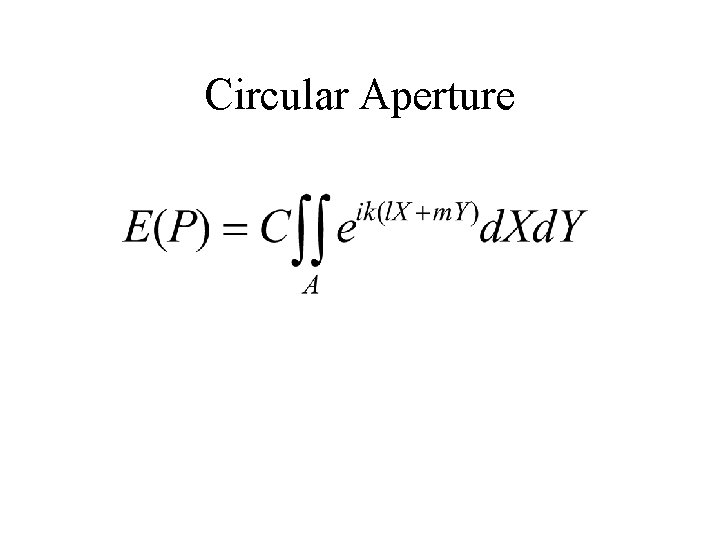
Circular Aperture

Airy disk 2 I = I 0 [2 J 1(γ) / γ] γ = π D Sin θ/ λ 2 [ J 1(γ) / γ] First minimum = 1. 22 π

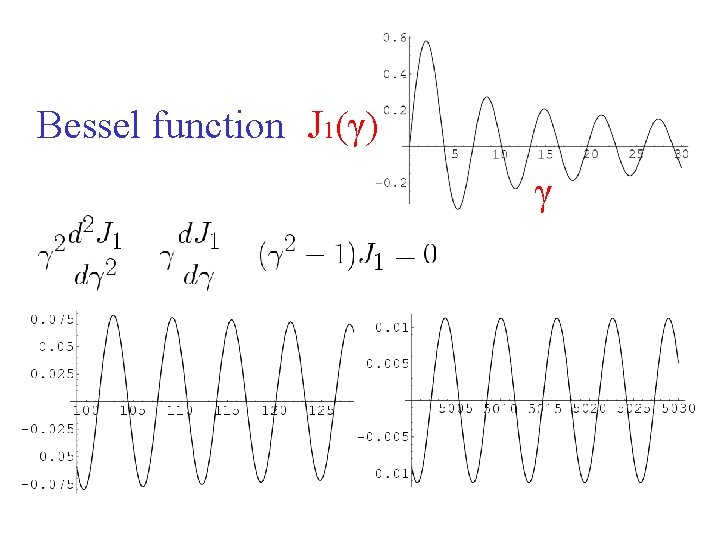
Bessel function J 1(γ) γ

Just resolved

Not resolved Well resolved

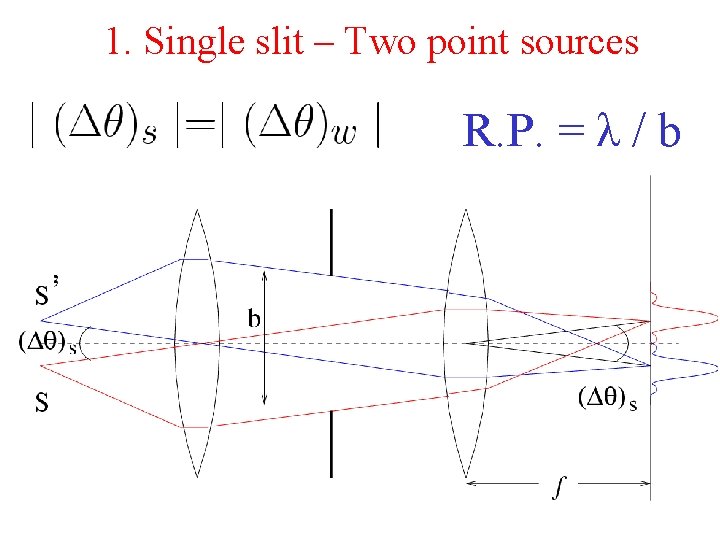
1. Single slit – Two point sources R. P. = λ / b

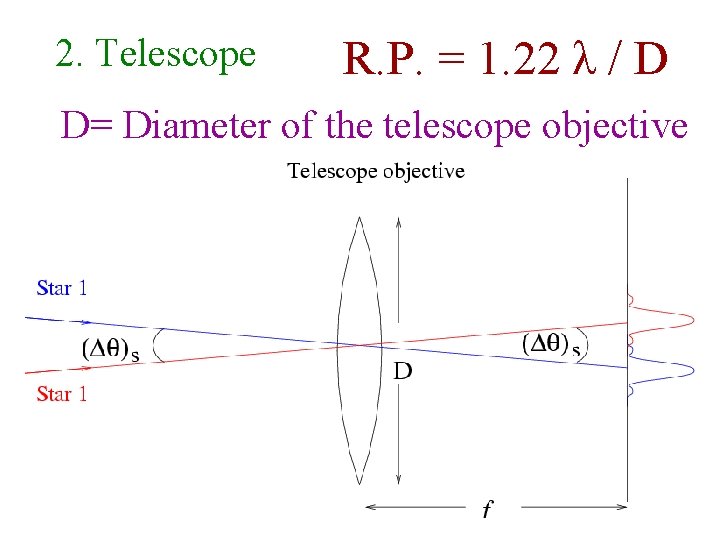
2. Telescope R. P. = 1. 22 λ / D D= Diameter of the telescope objective

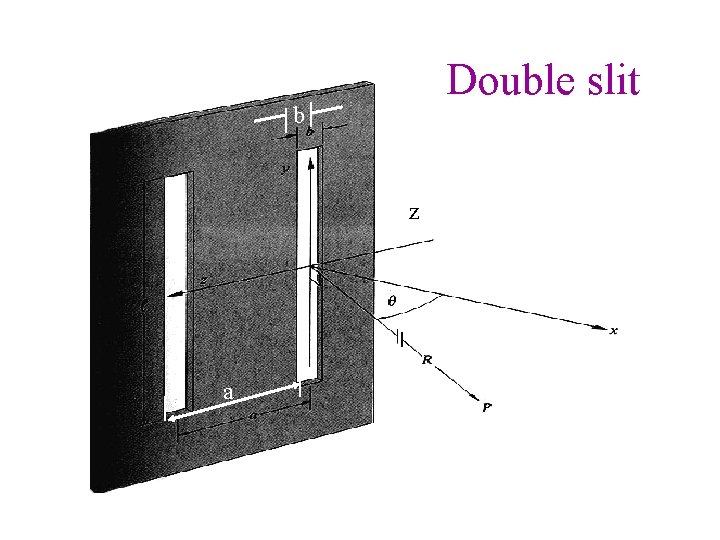
Double slit b z a

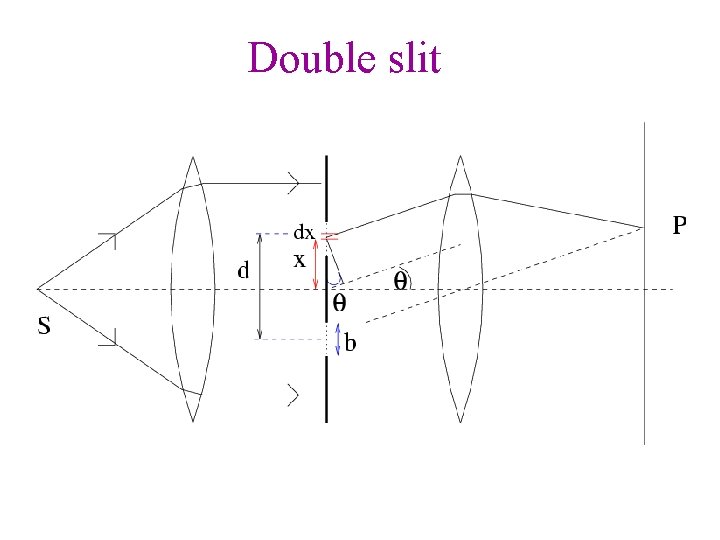
Double slit

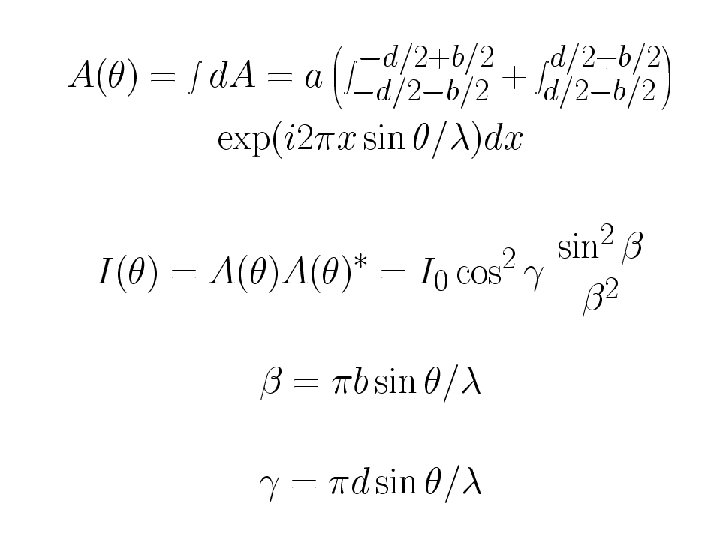
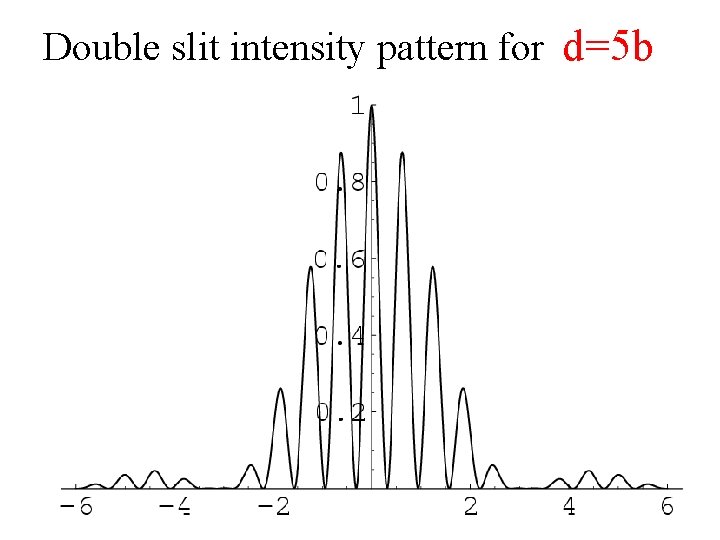
Double slit intensity pattern for d=5 b

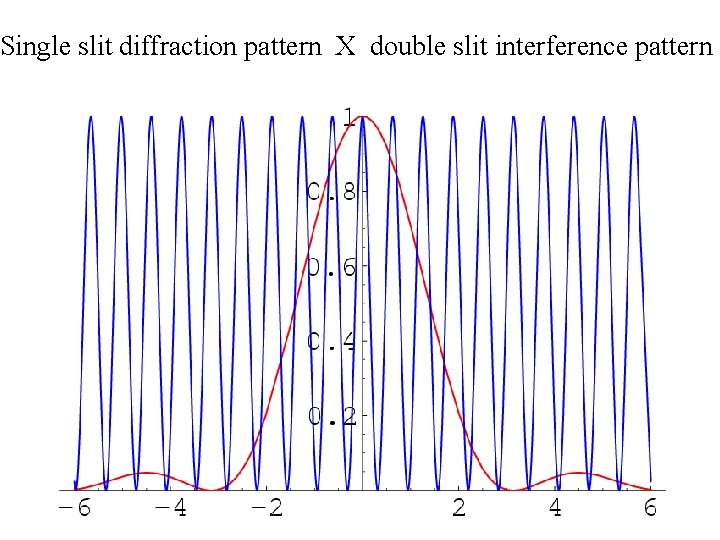
Single slit diffraction pattern X double slit interference pattern

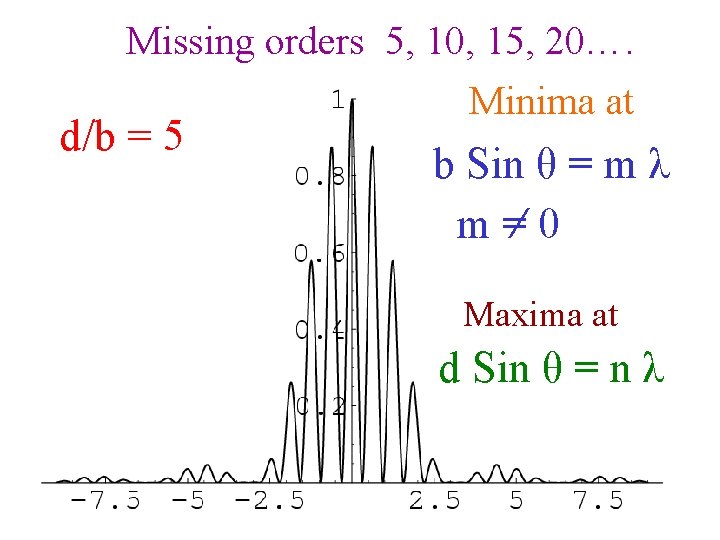
Missing orders 5, 10, 15, 20…. d/b = 5 Minima at b Sin θ = m λ m =/ 0 Maxima at d Sin θ = n λ

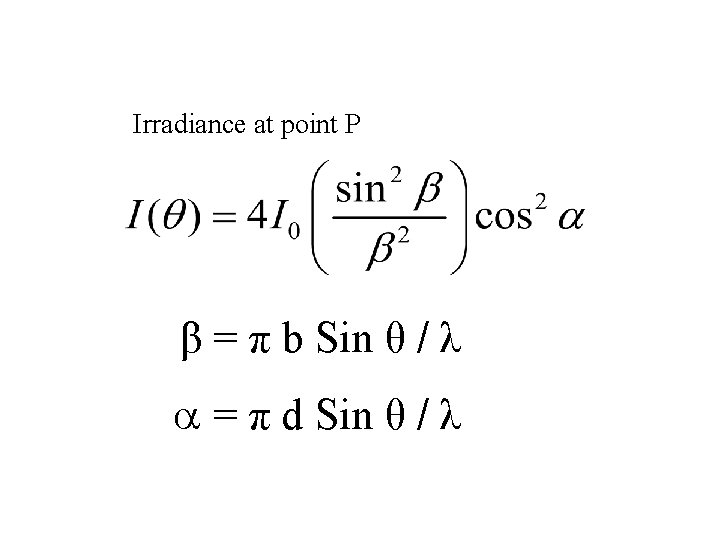
Irradiance at point P β = π b Sin θ / λ = π d Sin θ / λ

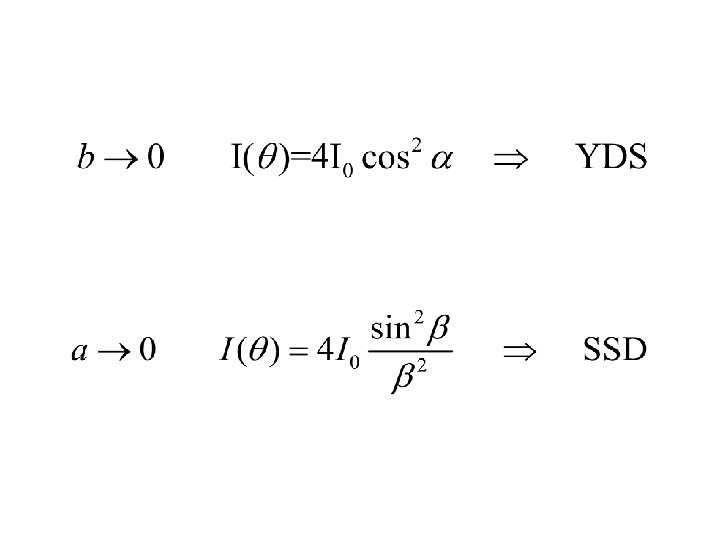
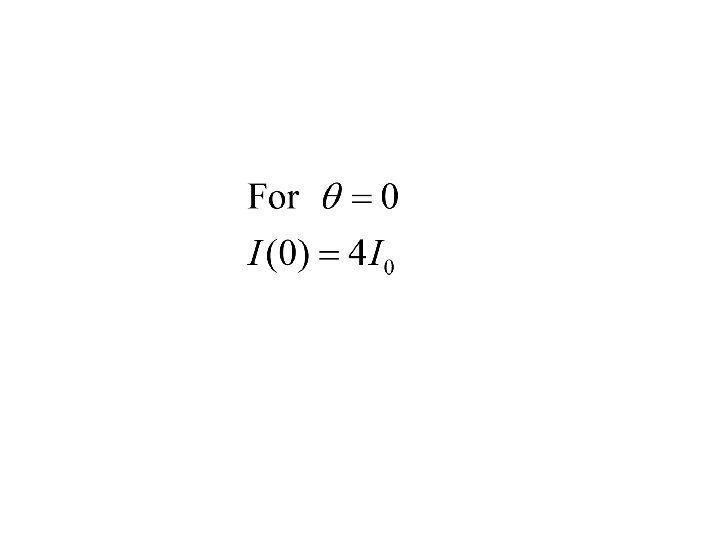
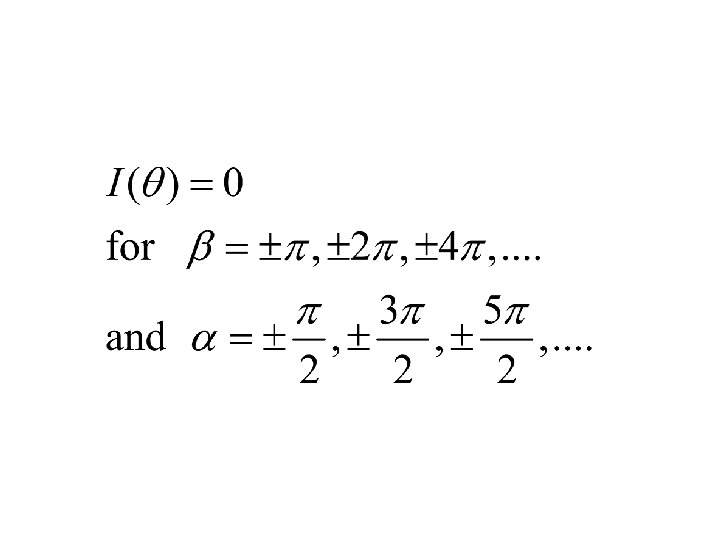
When we use the double-source equation to find locations of bright spots, we find that there are some places where we expect to see bright spots, but we see no light. This is known as a missing order, and it happens because at that location there's a zero in the single slit pattern.

Remember! If the zero in the single slit pattern, and a zero in the double slit pattern coincides, it is not called a missing order. . for, there is no order to be missing! Also, if there is a local peak in the single slit pattern, and a zero in the double source pattern, there will still be a zero (remember, we multiply the functions!) - this also is not a missing order.

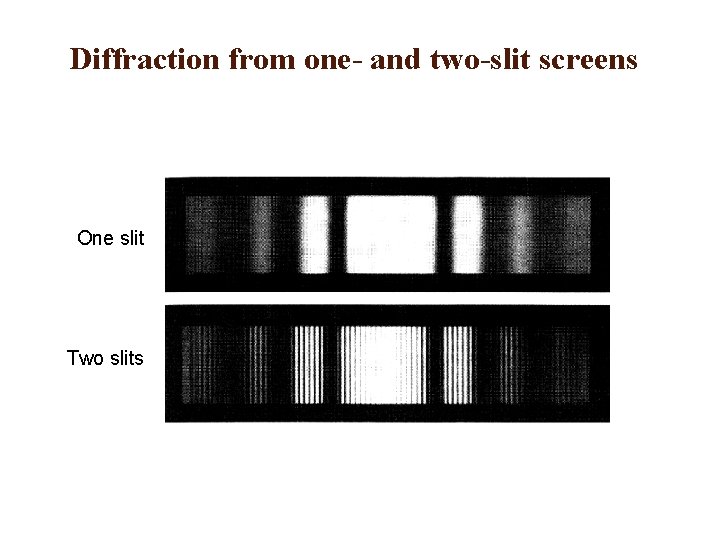
Diffraction from one- and two-slit screens One slit Two slits