f MRI Biological Basis and Experiment Design Lecture
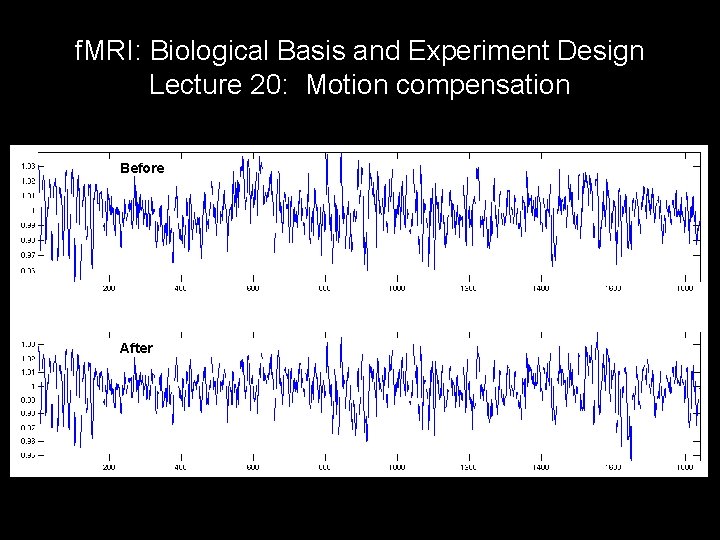
f. MRI: Biological Basis and Experiment Design Lecture 20: Motion compensation Before After 1 light year = 5, 913, 000, 000 miles? • Rotation matrices • Effects on data • Examples
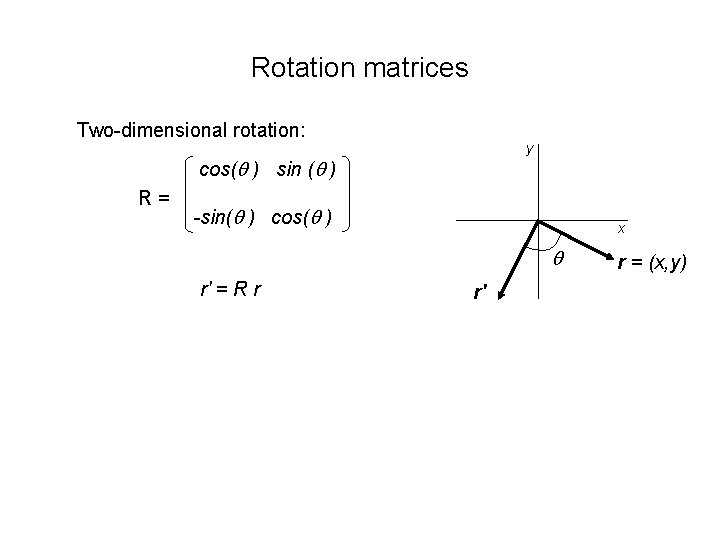
Rotation matrices Two-dimensional rotation: y cos( ) sin ( ) R= -sin( ) cos( ) x r' = R r r' r = (x, y)
![An aside: matrix multiplication y = Ax A is an [m x n] A An aside: matrix multiplication y = Ax A is an [m x n] A](http://slidetodoc.com/presentation_image_h2/ba3ea2e813cd459331f4bf0010f9afbc/image-3.jpg)
An aside: matrix multiplication y = Ax A is an [m x n] A 1, 1 A 1, 2 A 1, 3. . . A 1, n matrix: A 2, 1 A 2, 2 A 2, 3. . . A 2, n A 3, 1 A 3, 2 A 3, 3. . . A 3, n. . . Am, 1 Am, 2 Am, 3. . . Am, n x is an [n x p] x 1, 1 matrix: x 2, 1 x 3, 1. . . xn, 1 x 1, 2 x 2, 2 x 3, 2 xm, 2
![An aside: matrix multiplication A is [m x n] x is [n x p] An aside: matrix multiplication A is [m x n] x is [n x p]](http://slidetodoc.com/presentation_image_h2/ba3ea2e813cd459331f4bf0010f9afbc/image-4.jpg)
An aside: matrix multiplication A is [m x n] x is [n x p] A 1, 1 A 1, 2 A 1, 3. . . A 1, n A 2, 1 A 2, 2 A 2, 3. . . A 2, n A 3, 1 A 3, 2 A 3, 3. . . A 3, n. . . Am, 1 Am, 2 Am, 3. . . Am, n x x 1, 1 x 2, 1 x 3, 1. . . xn, 1 x 1, 2 x 2, 2 x 3, 2 xm, 2 y is [m x p] =

Rotation matrices Two-dimensional rotation: y cos( ) sin ( ) R= -sin( ) cos( ) x r' = R r cos( ) sin ( ) r' = -sin( ) cos( ) r' x cos( ) + y sin ( ) x = y -x sin( ) + y cos( ) r = (x, y)

Rotation example: 45 degree rotation of r = (1, 1) Two-dimensional rotation: y cos(45 ) sin (45 ) R= r = (1, 1) = 45 -sin(45 ) cos(45 ) x r' = ( 2, 0) r' = R r 1/ 2 r' = 1/ 2 - 1/ 2 + 1/ 2 1 x = 1 -1/ 2 + 1/ 2 2/ 2 = 0
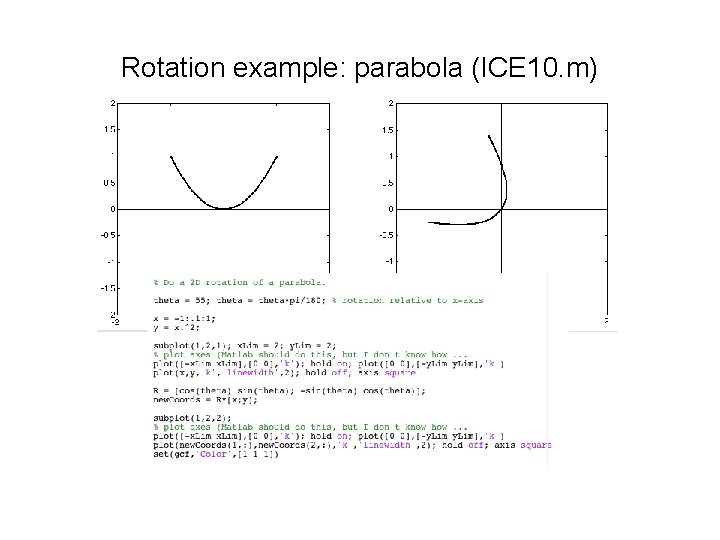
Rotation example: parabola (ICE 10. m)

Three dimensional rotation Excerpt from Wolfram Math. World
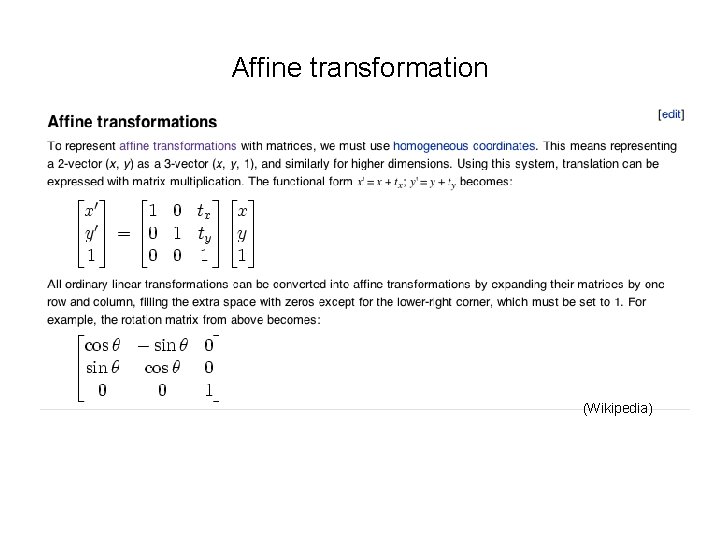
Affine transformation (Wikipedia)
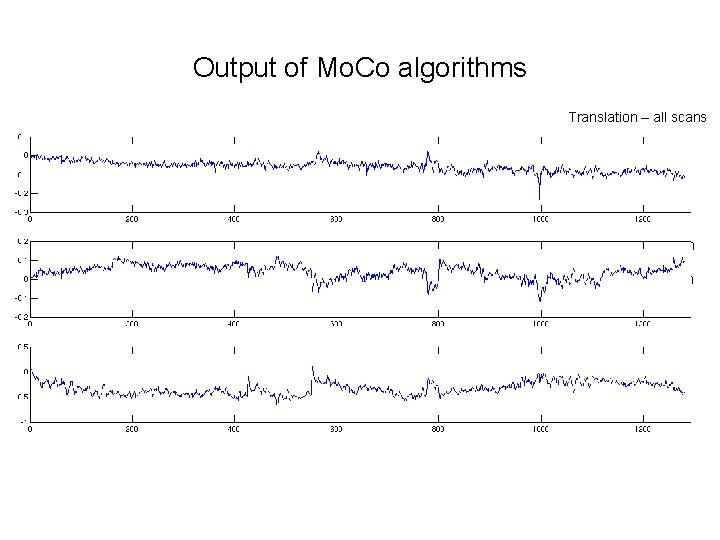
Output of Mo. Co algorithms Translation – all scans Translation – one scan Strong activation affects center of mass calculation

Effect of Mo. Co – increased activation size Before After
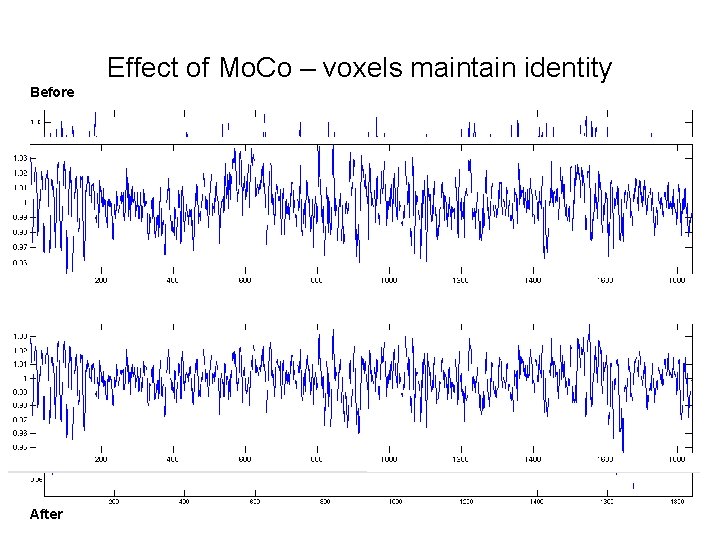
Effect of Mo. Co – voxels maintain identity Before After
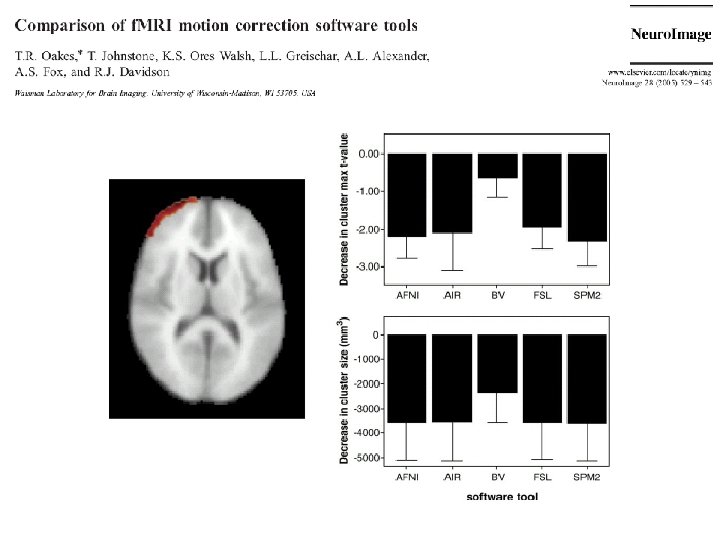
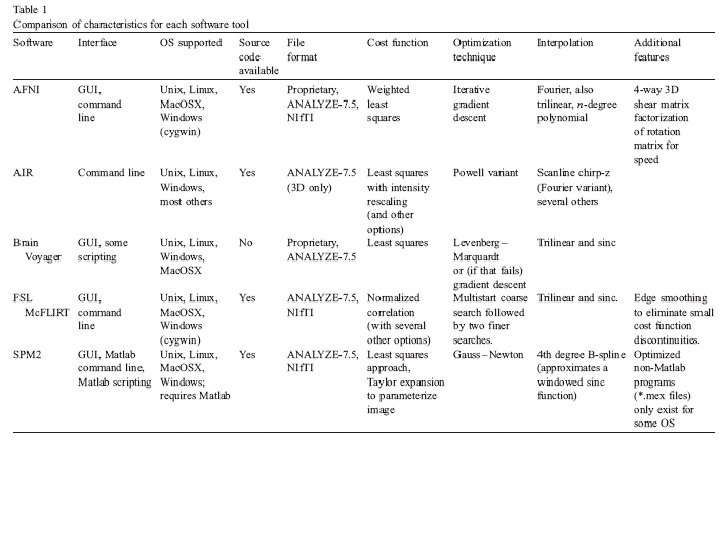
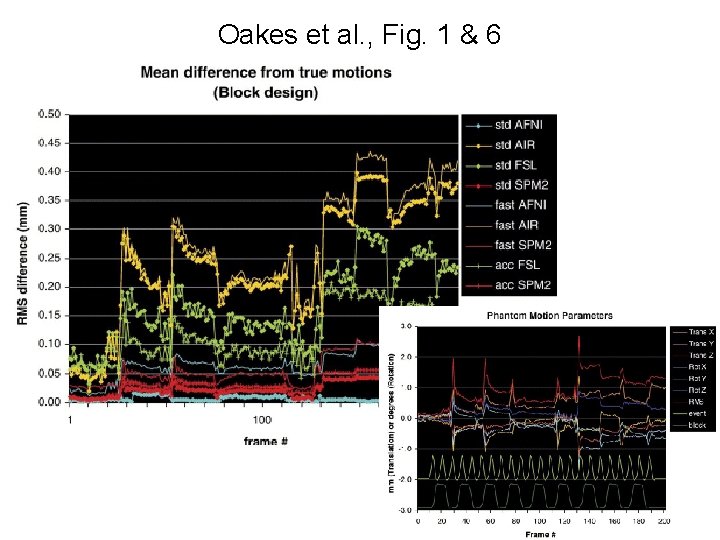
Oakes et al. , Fig. 1 & 6

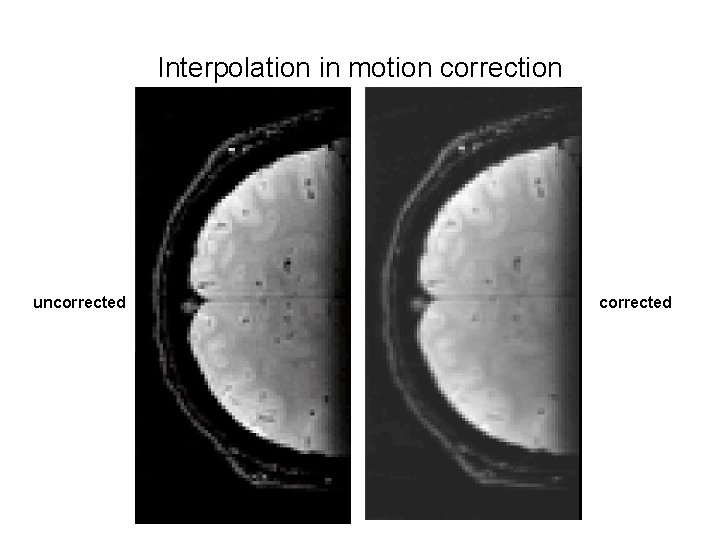
Interpolation in motion correction uncorrected
- Slides: 17