F 520 Options 1 Options F 520 Options

F 520 Options 1 Options

F 520 Options 2 Financial options contracts l l l An option is a right (rather than a commitment) to buy or sell an asset at a pre-specified price The right to purchase is a call option; the right to sell is a put option The strike price (or exercise price) is the price at which an option can be exercised Options which can be exercised only at maturity are “European Options”; “American Options” can be exercise any time prior or at maturity Options can be traded on exchanges or OTC markets.

F 520 Options 3 Call Options l Buying a Call Option--Gives the purchaser the right, but not the obligation, to buy the underlying security from the writer of the option at a prespecified price » t=0 pay C l t=1 receive Max(0, PR-X) Writing a Call Option—Gives the writer the obligation to sell the underlying security at a prespecified price » t=0 receive C t=1 pay Max(0, PR-X) C = Call Premium PR = Price of underlying security X = Exercise Price

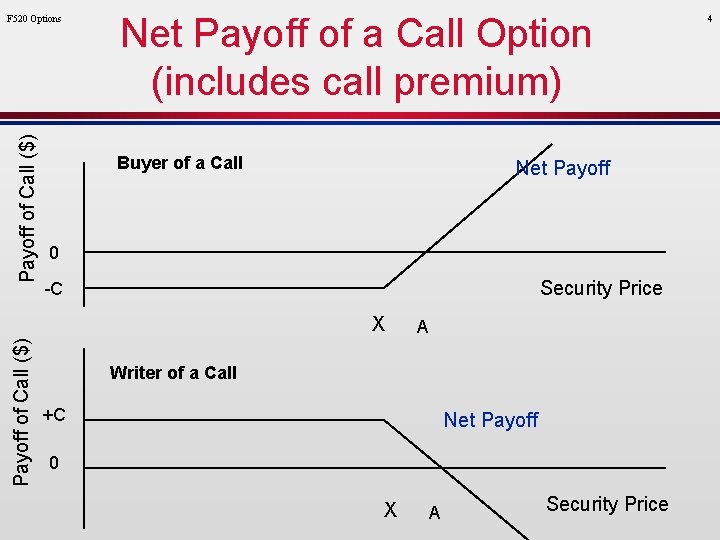
Payoff of Call ($) F 520 Options Net Payoff of a Call Option (includes call premium) Buyer of a Call Net Payoff 0 Security Price -C Payoff of Call ($) X A Writer of a Call +C Net Payoff 0 X A Security Price 4

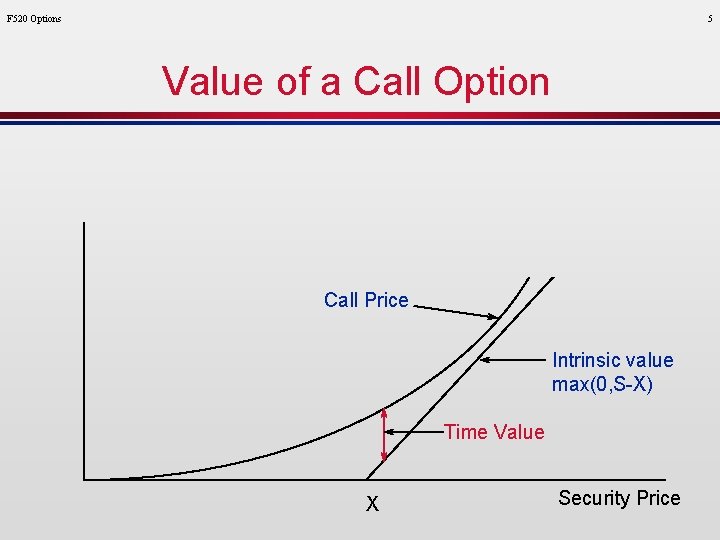
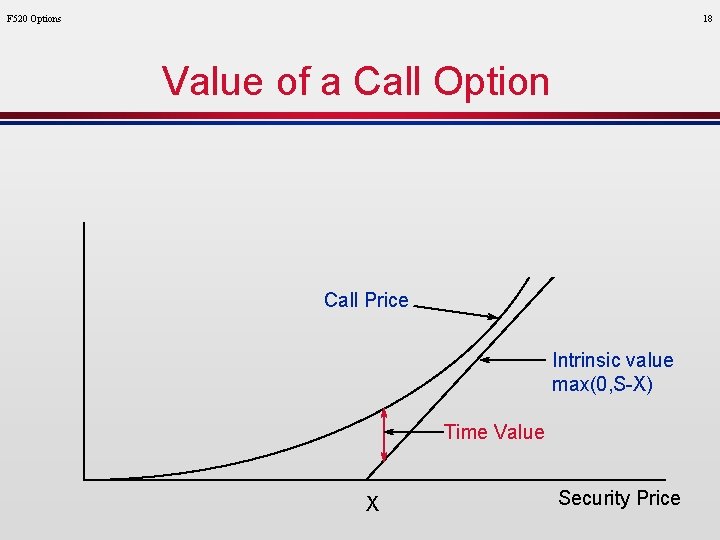
F 520 Options 5 Value of a Call Option Call Price Intrinsic value max(0, S-X) Time Value X Security Price

F 520 Options 6 Put Options l Buying a Put Option - Gives the purchaser the right, not the obligation, to sell the underlying security to the writer of the option at a pre-specified exercise price. » t=0 pay P l t=1 receive Max(0, X-PR) Writing a Put Option - Gives the writer the obligation to buy the underlying security at a prespecified price. » t=0 receive P P = Put Premium t=1 pay Max(0, X-PR)

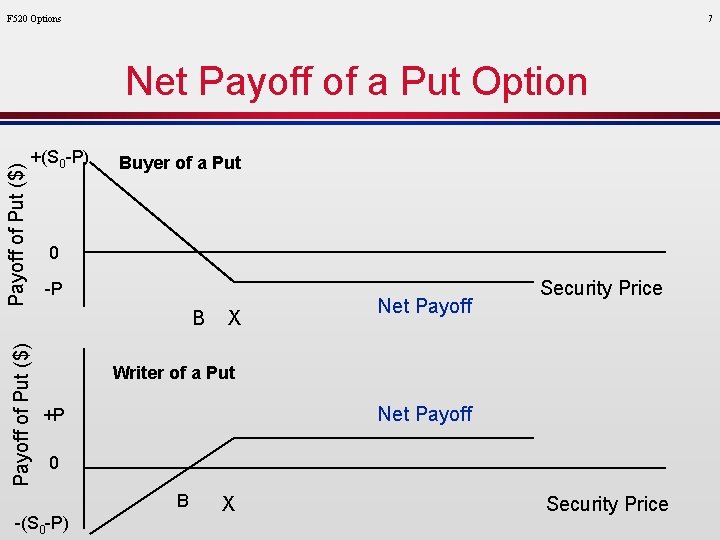
F 520 Options 7 +(S 0 -P) Payoff of Put ($) Net Payoff of a Put Option Buyer of a Put 0 -P B X Net Payoff Security Price Writer of a Put Net Payoff +P 0 B -(S 0 -P) X Security Price

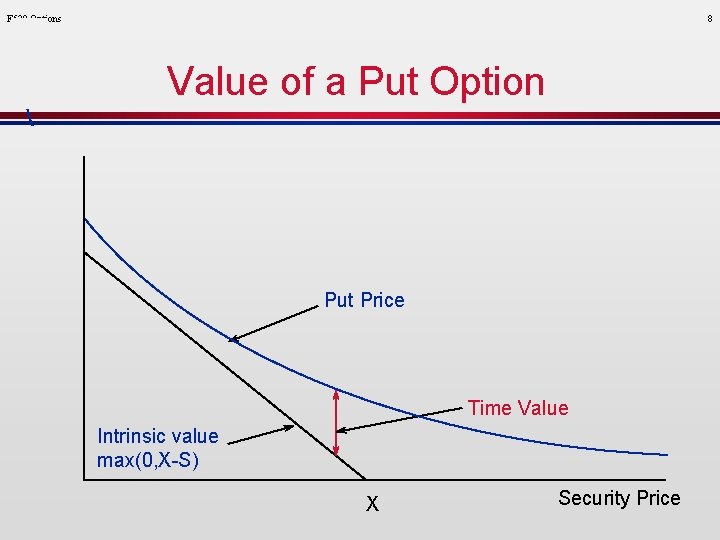
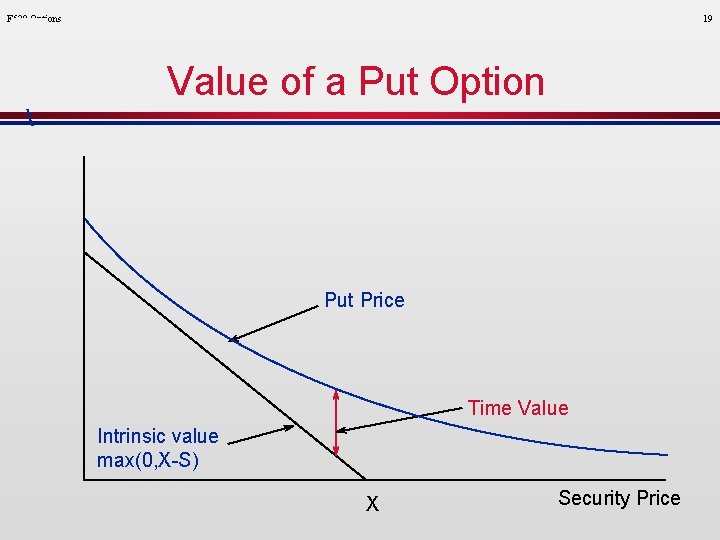
F 520 Options 8 Value of a Put Option Put Price Time Value Intrinsic value max(0, X-S) X Security Price

F 520 Options 9 Caps, Floors, and Collars l l l A cap is a call option where the seller guarantees to pay the buyer when the designated reference price exceed a predetermined cap price. The buyer pays a cap fee. A floor is a put option where the seller guarantees to pay the buyer when the designated reference price falls below a predetermined floor price. The buyer pays a floor fee. A collar is a position that simultaneously buys a cap and sells a floor.

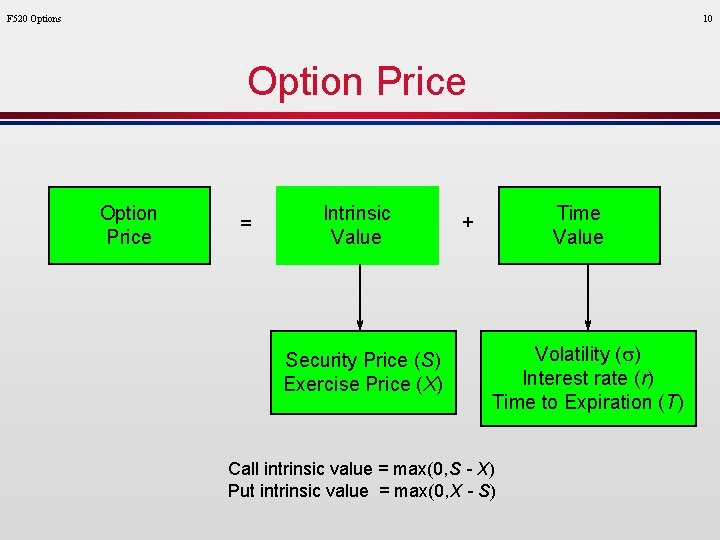
F 520 Options 10 Option Price = Intrinsic Value Security Price (S) Exercise Price (X) Time Value + Volatility (s) Interest rate (r) Time to Expiration (T) Call intrinsic value = max(0, S - X) Put intrinsic value = max(0, X - S)

F 520 – Futures http: //www. lme. com/metals/non-ferrous/copper/ 11

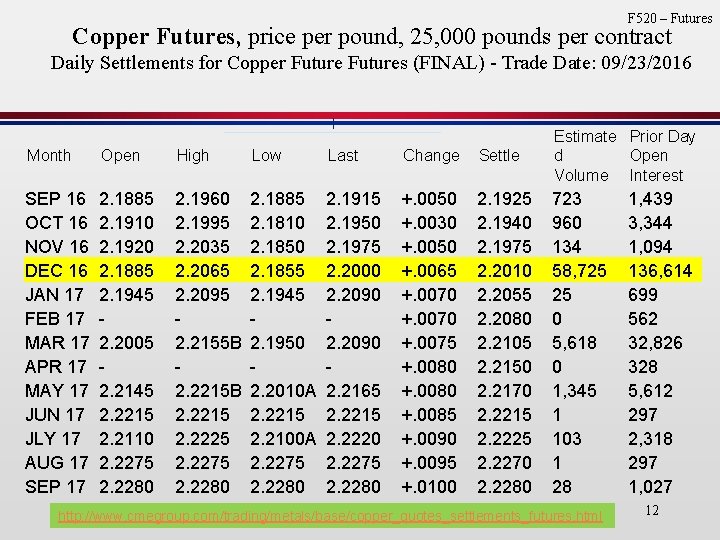
F 520 – Futures Copper Futures, price per pound, 25, 000 pounds per contract Daily Settlements for Copper Futures (FINAL) - Trade Date: 09/23/2016 | Month Open High Low Last Change Settle Estimate Prior Day d Open Volume Interest SEP 16 OCT 16 NOV 16 DEC 16 JAN 17 FEB 17 MAR 17 APR 17 MAY 17 JUN 17 JLY 17 AUG 17 SEP 17 2. 1885 2. 1910 2. 1920 2. 1885 2. 1945 2. 2005 2. 2145 2. 2215 2. 2110 2. 2275 2. 2280 2. 1960 2. 1995 2. 2035 2. 2065 2. 2095 2. 2155 B 2. 2215 2. 2225 2. 2275 2. 2280 2. 1885 2. 1810 2. 1855 2. 1945 2. 1950 2. 2010 A 2. 2215 2. 2100 A 2. 2275 2. 2280 2. 1915 2. 1950 2. 1975 2. 2000 2. 2090 2. 2165 2. 2215 2. 2220 2. 2275 2. 2280 +. 0050 +. 0030 +. 0050 +. 0065 +. 0070 +. 0075 +. 0080 +. 0085 +. 0090 +. 0095 +. 0100 2. 1925 2. 1940 2. 1975 2. 2010 2. 2055 2. 2080 2. 2105 2. 2150 2. 2170 2. 2215 2. 2225 2. 2270 2. 2280 723 960 134 58, 725 25 0 5, 618 0 1, 345 1 103 1 28 http: //www. cmegroup. com/trading/metals/base/copper_quotes_settlements_futures. html 1, 439 3, 344 1, 094 136, 614 699 562 32, 826 328 5, 612 297 2, 318 297 1, 027 12

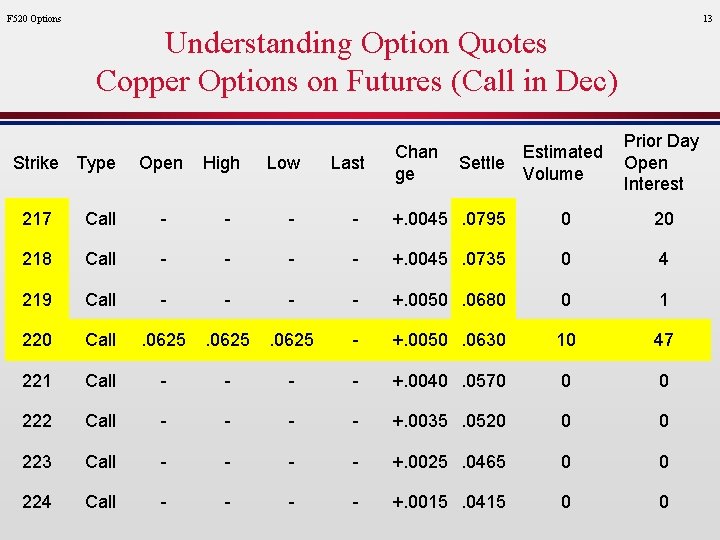
F 520 Options 13 Understanding Option Quotes Copper Options on Futures (Call in Dec) Strike Type Open High Low Last Chan ge Settle Estimated Volume Prior Day Open Interest 217 Call - - +. 0045. 0795 0 20 218 Call - - +. 0045. 0735 0 4 219 Call - - +. 0050. 0680 0 1 220 Call . 0625 - +. 0050. 0630 10 47 221 Call - - +. 0040. 0570 0 0 222 Call - - +. 0035. 0520 0 0 223 Call - - +. 0025. 0465 0 0 224 Call - - +. 0015. 0415 0 0

Understanding December Quotes Put in Dec F 520 Options l How much does it cost to purchase: » one call of Copper Futures Options contract (exercise price of 217)? Call =. 0795 / lb * 25, 000 lb per contract = $1, 987. 50 per contract l What is the intrinsic value of a call on Copper Futures Options (exercise price of 317)? Call = max(0, F-X) = max(0, 2. 20 – 2. 17) = 0. 03 cents Use the futures copper price (not the cash price) What is the time value of money? Option Price - Intrinsic Value = 0. 0795 – 0. 03 = 0. 0495 / lb l What is the intrinsic value of a call on Copper Futures Options (exercise price of 224)? Call = max(0, F-X) = max(0, 2. 20 – 2. 24) = 0 cents Use the futures copper price (not the cash price) What is the time value of money? Option Price - Intrinsic Value = 0. 0415 – 0 = 0. 0415 / lb l What is the intrinsic value of a call on Copper Futures Options (exercise price of 220)? Option Price - Intrinsic Value = 0. 0630 – 0 = 0. 0630 / lb l Why there greater intrinsic value for options near the money. 14

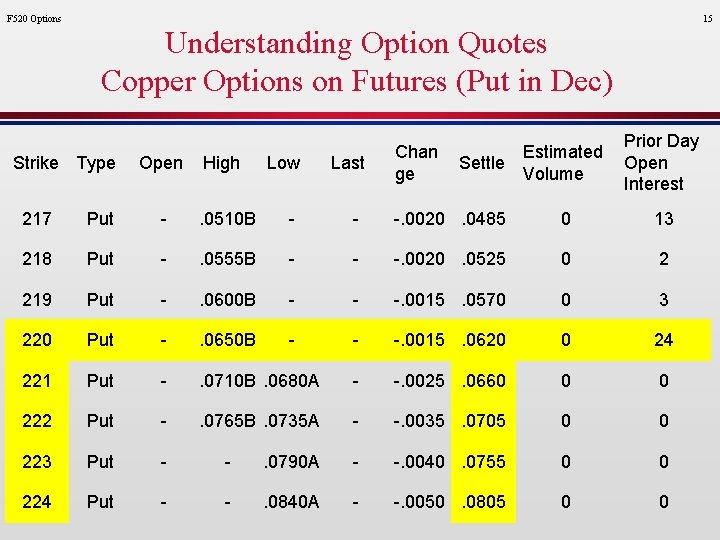
F 520 Options 15 Understanding Option Quotes Copper Options on Futures (Put in Dec) Strike Type Open High Low Last Chan ge Settle Estimated Volume Prior Day Open Interest 217 Put - . 0510 B - - -. 0020. 0485 0 13 218 Put - . 0555 B - - -. 0020. 0525 0 2 219 Put - . 0600 B - - -. 0015. 0570 0 3 220 Put - . 0650 B - - -. 0015. 0620 0 24 221 Put - . 0710 B. 0680 A - -. 0025. 0660 0 0 222 Put - . 0765 B. 0735 A - -. 0035. 0705 0 0 223 Put - - . 0790 A - -. 0040. 0755 0 0 224 Put - - . 0840 A - -. 0050. 0805 0 0

Understanding December Quotes Put in Dec F 520 Options l How much does it cost to purchase: » one put of Copper Futures Options contract (exercise price of 217)? Call =. 0485 / lb * 25, 000 lb per contract = $1, 212. 50 per contract l What is the intrinsic value of a put on Copper Futures Options (exercise price of 317)? Call = max(0, X-F) = max(0, 2. 17 – 2. 20) = 0. 0 cents Use the futures copper price (not the cash price) What is the time value of money? Option Price - Intrinsic Value = 0. 0485 – 0. 0 = 0. 0485 / lb l What is the intrinsic value of a put on Copper Futures Options (exercise price of 224)? Call = max(0, X-F) = max(0, 2. 24 – 2. 20) = 0. 04 cents Use the futures copper price (not the cash price) What is the time value of money? Option Price - Intrinsic Value = 0. 0805 – 0. 040 = 0. 0405 / lb l What is the intrinsic value of a put on Copper Futures Options (exercise price of 220)? Option Price - Intrinsic Value = 0. 0620 – 0 = 0. 0620 / lb l Why there greater intrinsic value for options near the money. 16

F 520 Options 17 Understanding Option Prices Option Price = Intrinsic Value Security Price (S) Exercise Price (X) Time Value + Volatility (s) Interest rate (r) Time to Expiration (T) Call intrinsic value = max(0, S - X) Put intrinsic value = max(0, X - S)

F 520 Options 18 Value of a Call Option Call Price Intrinsic value max(0, S-X) Time Value X Security Price

F 520 Options 19 Value of a Put Option Put Price Time Value Intrinsic value max(0, X-S) X Security Price

The Black-Scholes Option Pricing Model F 520 Options l The B-S option pricing model for a call is: C = S 0 - Xe-r. T + P C = S 0 N(d 1) - Xe-r. TN(d 2) where d 1 = [ln(S/X)+(r+ ½s 2)T]/sÖT d 2 = d 1 - sÖT N(d) = cumulative normal distribution 20

F 520 Options 21 Black-Scholes Put Price l Price of a European put is: P = C - S 0 + Xe-r. T = S 0[N(d 1)-1] - Xe-r. T[N(d 2)-1] where d 1, d 2, and N(d) are defined as before.

F 520 Options 22 Black-Scholes Pricing Example l Assume: » » » l C S 0 = $100 d 1 X = $100 d 1 r = 5% d 1 s = 22% d 2 T = 1 year d 2 = S 0 N(d 1) - Xe-r. TN(d 2) = [ln(S/X)+(r+ ½s 2)T]/sÖT = [ln(100/100)+(. 05+ ½(0. 22)2)1]/(0. 22)Ö 1 = 0 +. 0742/. 22 =. 337274 = d 1 - sÖT =. 33727 - 0. 22/Ö 1 =. 117273 Then: » d 1 = 0. 34, » d 2 = 0. 12 N(d 1) = 0. 6331 N(d 2) = 0. 5478

F 520 Options 23 Call Option Example l l l Price of a call is then: C = S 0 N(d 1) - Xe-r. TN(d 2) C= 100(0. 6331) - 100(0. 9512)(0. 5478) = $11. 20 Price of a put is then: P = S 0[N(d 1)-1] - Xe-r. T[N(d 2)-1] P = 100[. 6331 - 1] - 100(1/e(. 05*1))(. 5478 -1) P = 100(-0. 3669) - 100(0. 9512)(-0. 4522) = $6. 32 Double check through Put-Call Parity: P = C - S 0 + Xe-r. T 6. 32 = 11. 20 – 100 + 100(0. 9512)

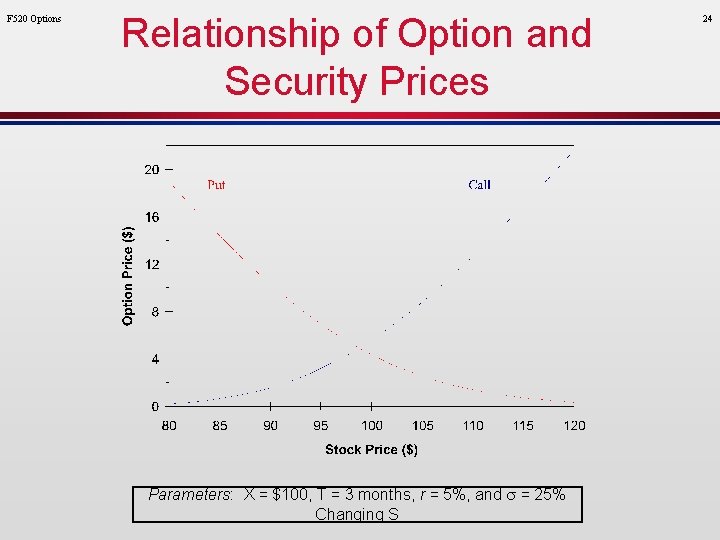
F 520 Options Relationship of Option and Security Prices Parameters: X = $100, T = 3 months, r = 5%, and s = 25% Changing S 24

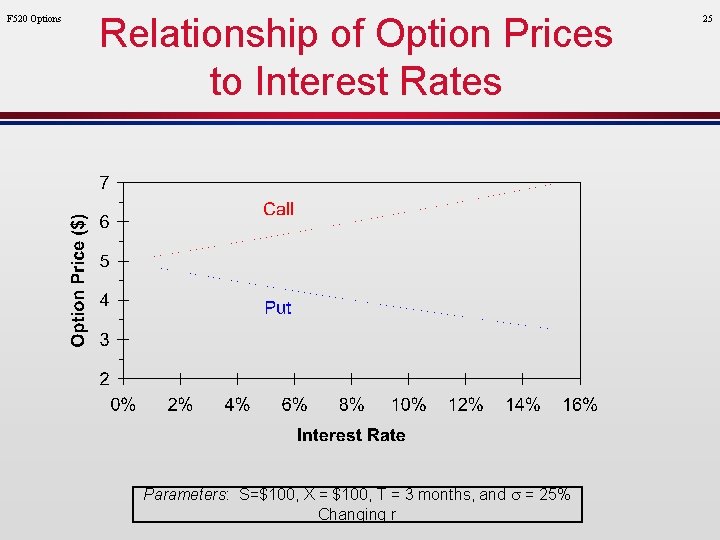
F 520 Options Relationship of Option Prices to Interest Rates Parameters: S=$100, X = $100, T = 3 months, and s = 25% Changing r 25

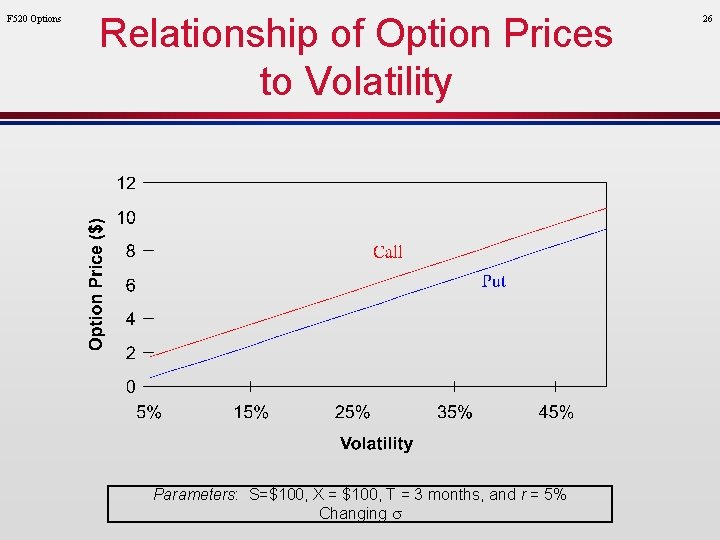
F 520 Options Relationship of Option Prices to Volatility Parameters: S=$100, X = $100, T = 3 months, and r = 5% Changing s 26

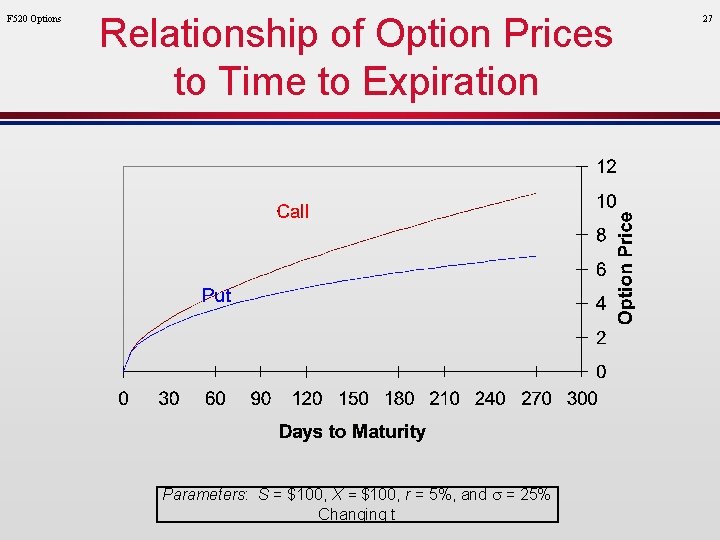
F 520 Options Relationship of Option Prices to Time to Expiration Parameters: S = $100, X = $100, r = 5%, and s = 25% Changing t 27

F 520 Options l Parameters of the Black-Scholes Model Need to know: » S, X, r, T, s. l l All readily observable, except the last. The interest rate should be a continuously compounded rate » To convert simple annualized rate to continuously compounded rate: r = ln(1+R) 28

F 520 Options 29 Volatility as a Parameter l l In pricing options, analysts usually use some measure of historical volatility of the underlying security. Volatility obtained from other than annualized returns must be converted to annualized volatility. » e. g. , Variance of weekly returns must be multiplied by 52. » e. g. , Standard deviation of weekly returns must be multiplied by Ö 52.

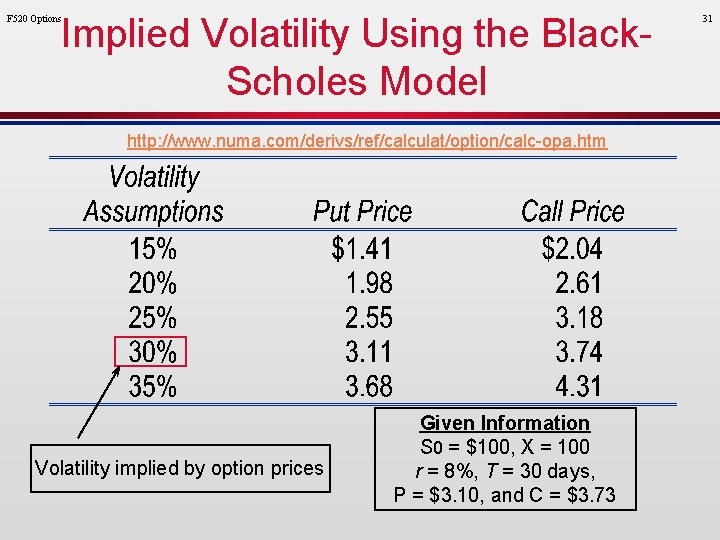
F 520 Options 30 Implied Volatility l Alternatively, can use all the other inputs, and infer a volatility estimate from the current option price. » Is called the implied volatility. l Can then compare implied volatility with recent historical volatility. » Higher implied than historical may indicate the option is expensive. » Lower implied than historical may indicate the option is cheap.

Implied Volatility Using the Black. Scholes Model F 520 Options http: //www. numa. com/derivs/ref/calculat/option/calc-opa. htm Volatility implied by option prices Given Information S 0 = $100, X = 100 r = 8%, T = 30 days, P = $3. 10, and C = $3. 73 31

F 520 Options l l l Assumptions In Original Option Pricing Model Underlying returns log normally distributed. Variance is constant over time. The interest rate is constant over time. No sudden jumps in underlying price. No dividends. No early exercise (i. e. , European option). 32

F 520 Options l l l Enhancing Firm Value through Hedging Reducing Volatility of cash flows does not guarantee increased value. Hedging has transaction costs, so hedging is not free. Hedging can add value if » Taxes are reduced » Transaction costs (like default risk) is reduced » When it aligns incentives to take positive NPV projects 33

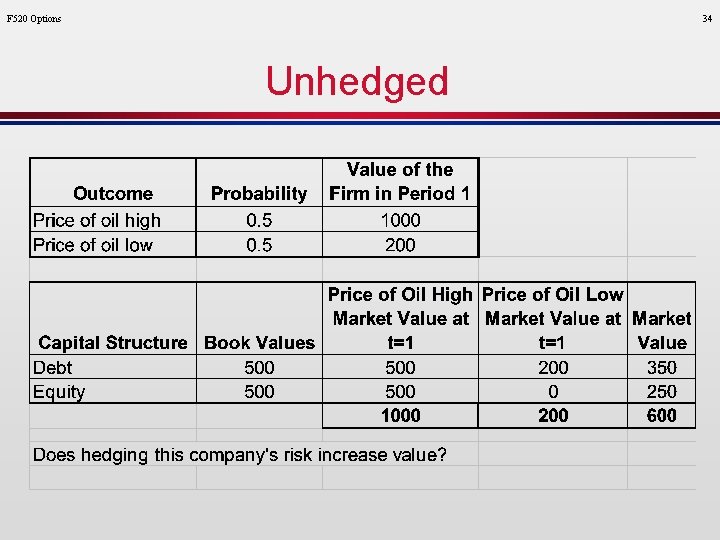
F 520 Options 34 Unhedged

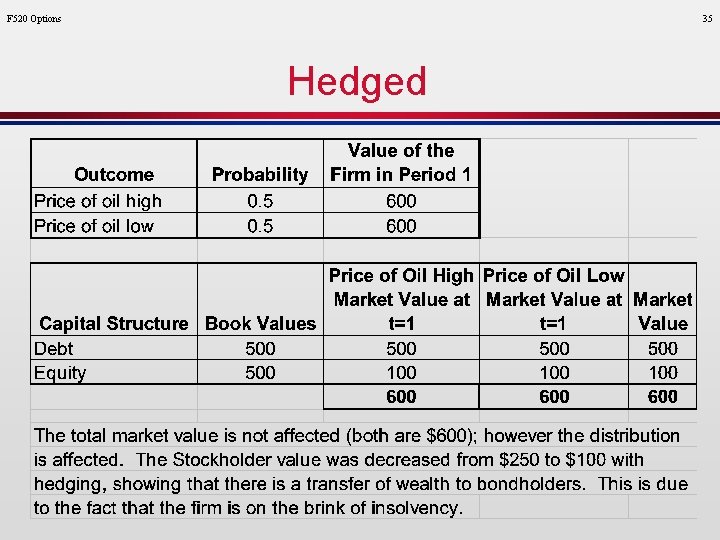
F 520 Options 35 Hedged

Payoff on Firm ($) F 520 Options Note the similarities between the payoff on stock and a call option. Buyer of a Call / Stock Net Payoff 0 -C X = Debt Amount Market Value of Assets In our prior example, stockholders only get paid after the debtholders receive their value. Therefore, the value of the debt is like the exercise price on a call option. If the value of the firm is less than the value of the debt, stockholders will walk away and leave the firm to the debtholders. If the value of the firm is greater than the value of the debt, the stockholders remain in control of the firm. This also shows why reducing volatility (through hedging) does not guarantee an increase in the value of the firm. In fact, as shown in the Black Scholes formula, decreasing volatility can reduce the value of the firm to equity holders (see the hedging example several slides earlier. 36

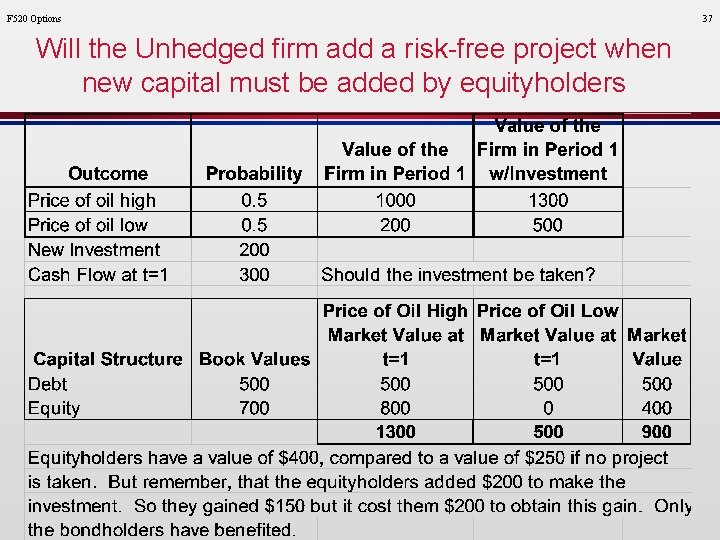
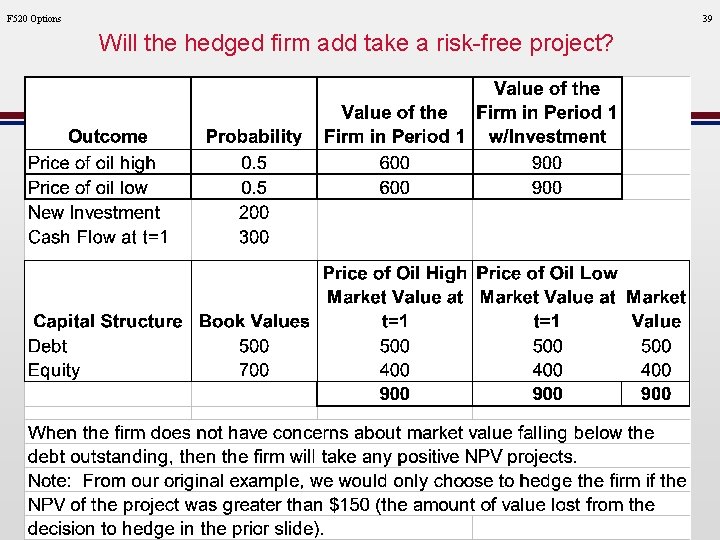
F 520 Options Will the Unhedged firm add a risk-free project when new capital must be added by equityholders 37

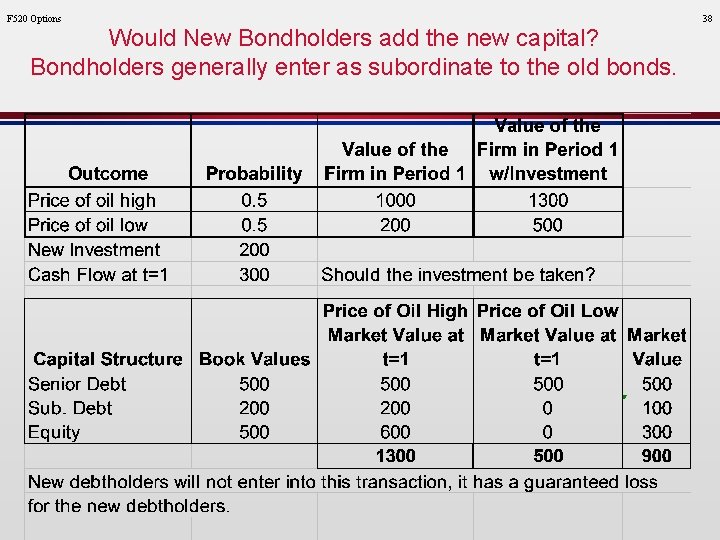
F 520 Options Would New Bondholders add the new capital? Bondholders generally enter as subordinate to the old bonds. 38

F 520 Options 39 Will the hedged firm add take a risk-free project?

F 520 Options 40 Swaps l l l A swap is an agreement whereby two parties (called counterparties) agree to exchange periodic payments. The dollar amount of the payments exchanged is based on some predetermined dollar principal (or commodity quantity), which is called the notional amount. It can be considered the same as entering a series of forward contracts, since it is an agreement to make the exchange at several points in the future. Types of swaps include » » » Interest rate swaps Interest rate-equity swaps Equity swaps Currency swaps Commodity swaps

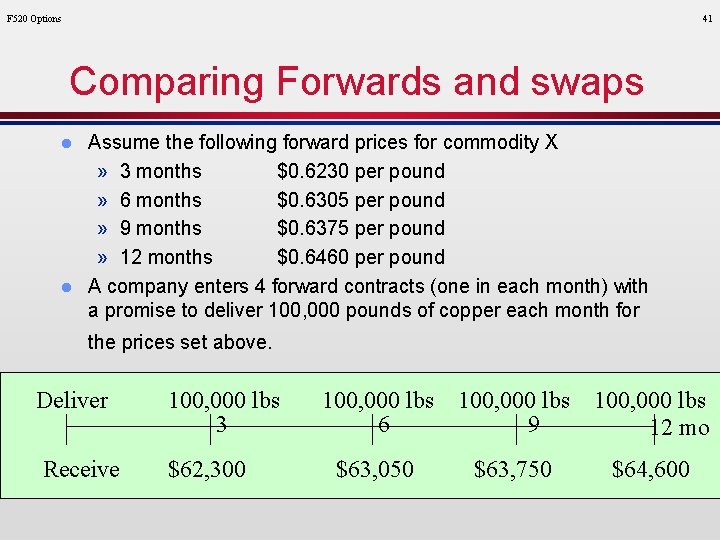
F 520 Options 41 Comparing Forwards and swaps l l Assume the following forward prices for commodity X » 3 months $0. 6230 per pound » 6 months $0. 6305 per pound » 9 months $0. 6375 per pound » 12 months $0. 6460 per pound A company enters 4 forward contracts (one in each month) with a promise to deliver 100, 000 pounds of copper each month for the prices set above. Deliver 100, 000 lbs 3 6 9 12 mo Receive $62, 300 $63, 050 $63, 750 $64, 600

F 520 Options 42 Calculating swap payment l l l Find the Present Value of the Cash Flows (assume 2% per quarter) PV = $62, 300/(1. 02)1 + $63, 050/(1. 02)2 + $63, 750/(1. 02)3 + $64, 600/ /(1. 02)4 = $241, 433. 59 Now spread this value over 4 equal payments at the end of each period (4 period annuity). PV = $241, 433. 59, I = 2, N = 4, FV = 0, compute PMT = $63, 406. 19 A swap will have four equal payments of $63, 158. 72 at the end of each quarter. Deliver 100, 000 lbs 3 6 9 12 mo Receive $63, 406 $63, 406

F 520 Options 43 Using Duration in Hedging l l l Hedge the future issuance of 90 -day commercial paper. Assume today is August 10, 200 X. Our projected date of cash flow needs is November 25, 200 X. ü The amount of commercial paper that will be issued is $50 million. ü The Euro-dollar Futures contract has a face value of $1 million is if for a 90 -day maturity Eurodollar issue to be made 107 days from today. l Should you take a long or a short position?

F 520 Options Should you take a long or a short position? l You want to protect against rising interest rates that results in falling prices. Therefore, you want the futures contract to make money when prices fall (a short position). These profits from the futures contract will offset the lower set of funds your will be able to bring in if interest rates increase and you issue the commercial paper at a larger discount. l How many contracts do we need? 44

F 520 Options How many contracts do we need? Formula from Hedging notes: $ amt. of security duration of asset # of Contracts = -------------- X ------------ $ amt. of fut. contract duration of future sec $50, 000 90 -days # of Contracts = ------------ X ------------ = 50 $1, 000 90 -days contracts 45

F 520 Options 46 If commercial paper rates go up by 40 basis points (from 3. 53% to 3. 93%) and Eurodollar future rates also go up by 40 basis points (from 3. 565% to 3. 965), how much money will get from the futures contract and how much money will we get from our commercial paper issuance? Futures contract 40 bp * $25 per basis point *50 contracts = $50, 000 profit Commercial paper issuance: 1, 000 * (1 -. 0393*(90/360)) = $990, 175 x 50 contracts $49, 508, 750 This is exactly $50, 000 less than what we had anticipated raising if rates had remained at 3. 53%. Between the profits from the futures contract and the expected commercial paper issuance proceeds, we have locked in our expected cash flow. Now let’s just hope that our basis risk (difference between spot and futures prices) remains the same over this time period. Notes: ü The change in $1 million for a 1 bp interest rate change is equal to $1, 000*(. 0001*(90/360)) = $25 ü 1, 000 * (1 -. 0353*(90/360)) = $990, 175 x 50 contracts $49, 558, 750

F 520 Options How many contracts do we need? Situation 2 If we had a desire to issue commercial paper 107 days from now with 120 -days to maturity, how many contracts would we need? $50, 000 120 -days # of Contracts = ----------- X ----------- = 66. 67 $1, 000 90 -days contracts 47

F 520 Options 48 Contracts l Options and Futures http: //www. cmegroup. com/education/getting-started. html l Future and Option contracts http: //www. cmegroup. com/globex/ l www. cmegroup. com