Extreme value statistics Problems of extrapolating to values

Extreme value statistics Problems of extrapolating to values we have no data about unusually large or small ~100 years (data) ~500 years (design) winds Question: Can this be done at all? How long will it stand?

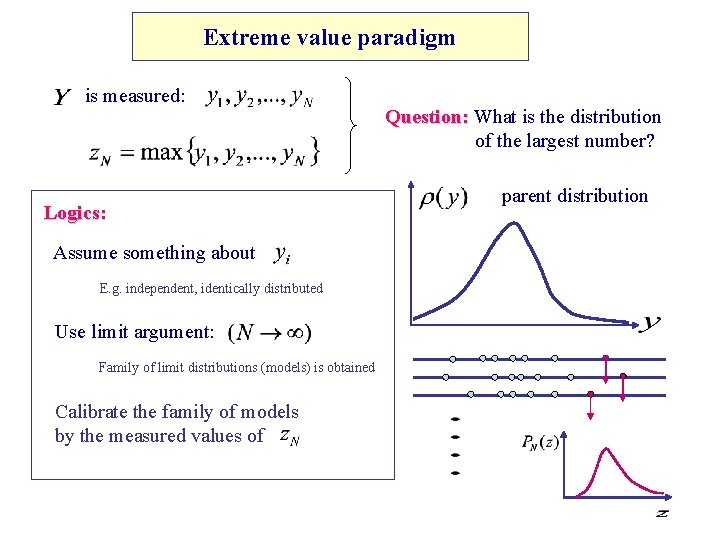
Extreme value paradigm is measured: Logics: Assume something about E. g. independent, identically distributed Use limit argument: Family of limit distributions (models) is obtained Calibrate the family of models by the measured values of Question: What is the distribution of the largest number? parent distribution

An example of extreme value statistics Data plots here and below are from Stuart Coles: An Introduction to Statistical Modeling of Extreme Values The 1841 sea level benchmark (centre) on the `Isle of the Dead', Tasmania. According to Antarctic explorer, Capt. Sir James Clark Ross, it marked mean sea level in 1841. Recurrence time: If then the maximum will exceed in T years.

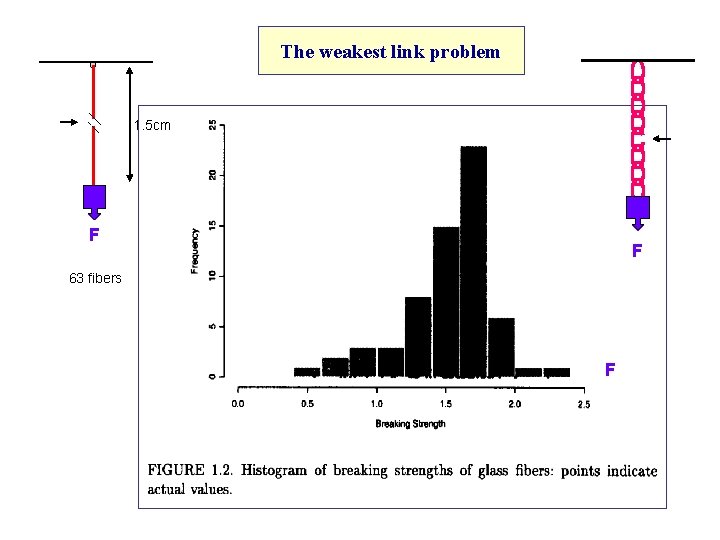
The weakest link problem 1. 5 cm F F 63 fibers F

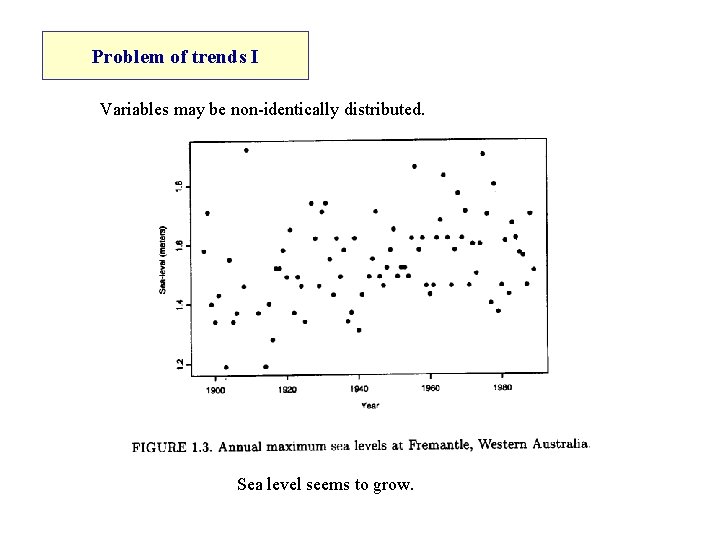
Problem of trends I Variables may be non-identically distributed. Sea level seems to grow.

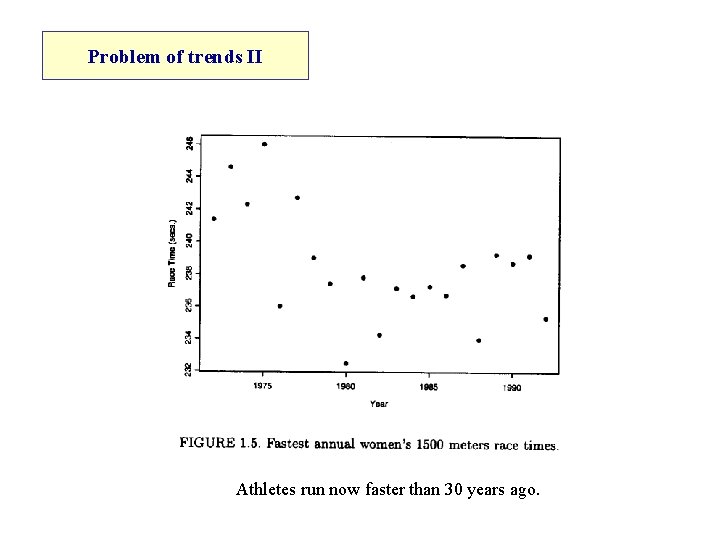
Problem of trends II Athletes run now faster than 30 years ago.

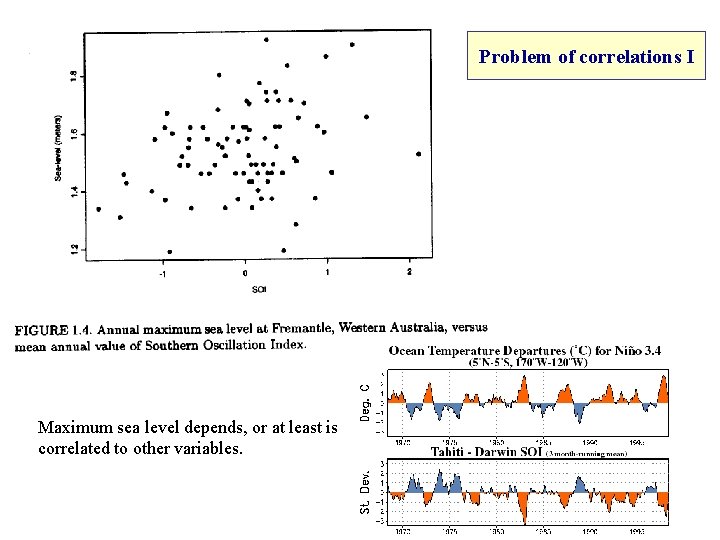
Problem of correlations I Maximum sea level depends, or at least is correlated to other variables.

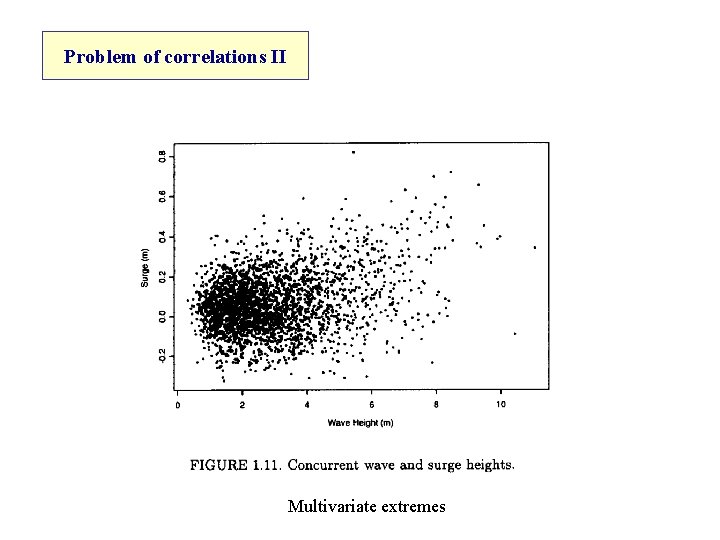
Problem of correlations II Multivariate extremes

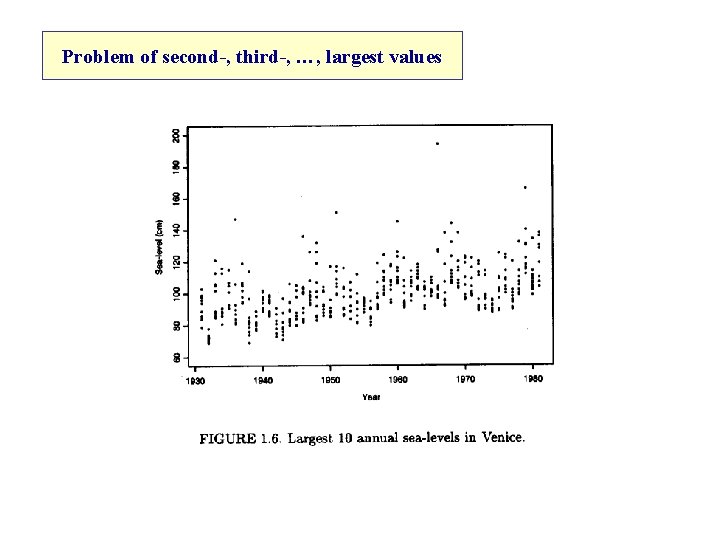
Problem of second-, third-, …, largest values

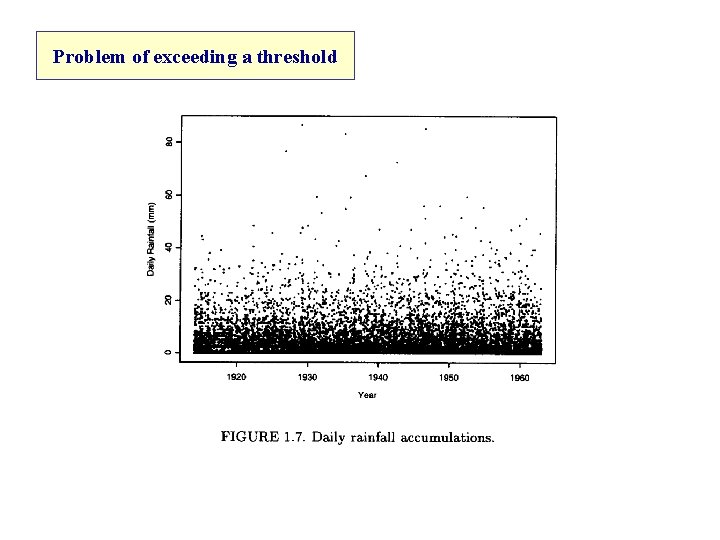
Problem of exceeding a threshold

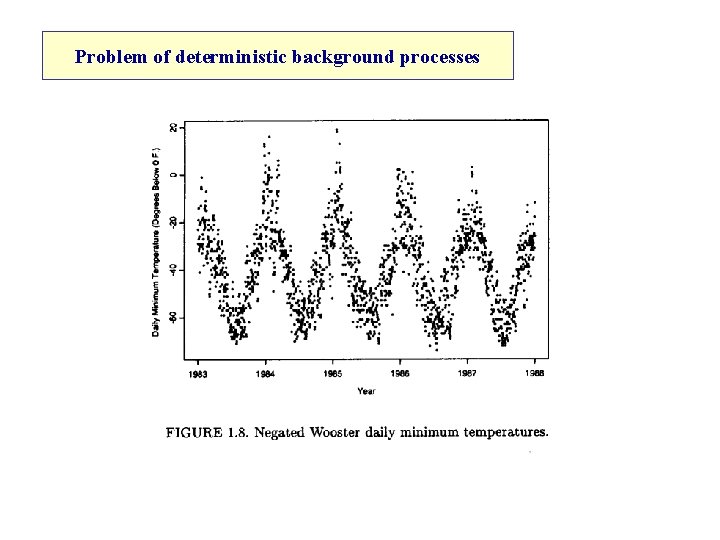
Problem of deterministic background processes

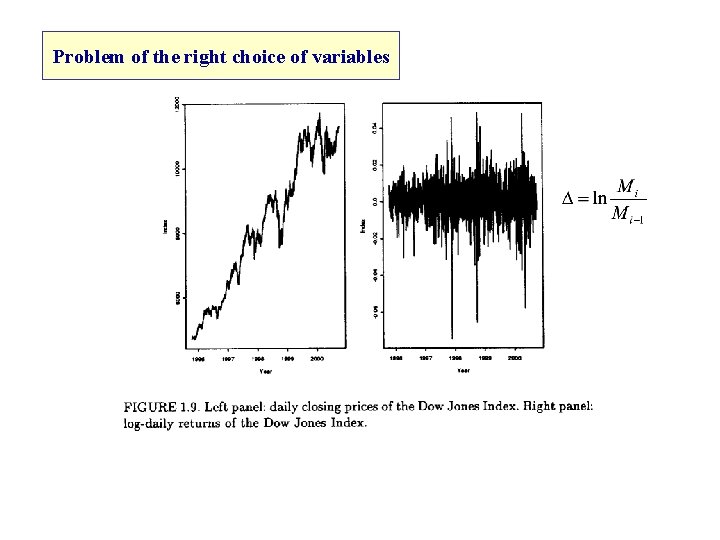
Problem of the right choice of variables

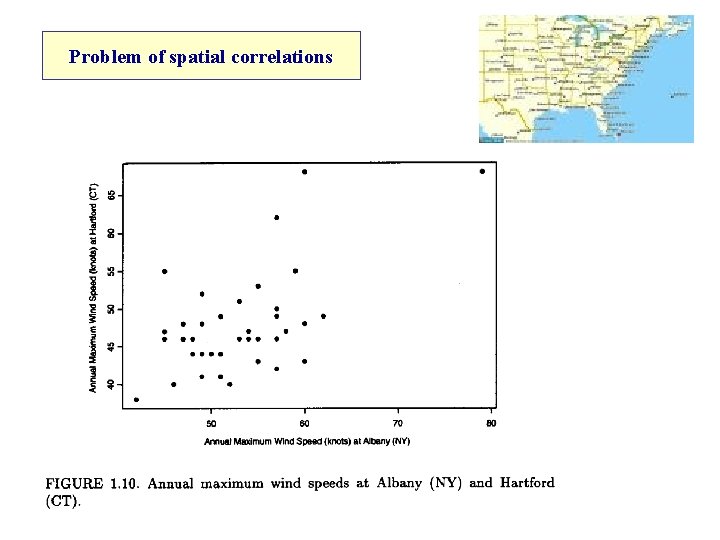
Problem of spatial correlations

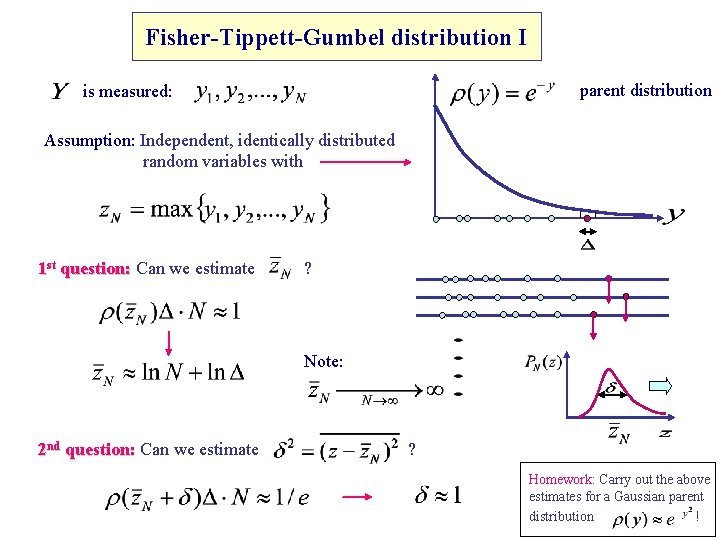
Fisher-Tippett-Gumbel distribution I parent distribution is measured: Assumption: Independent, identically distributed random variables with 1 st question: Can we estimate ? Note: 2 nd question: Can we estimate ? Homework: Carry out the above estimates for a Gaussian parent distribution !

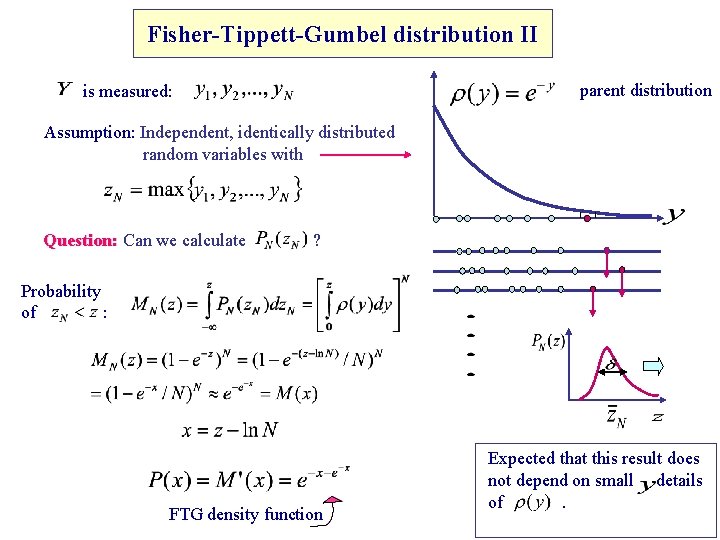
Fisher-Tippett-Gumbel distribution II parent distribution is measured: Assumption: Independent, identically distributed random variables with Question: Can we calculate ? Probability of : FTG density function Expected that this result does not depend on small details of.

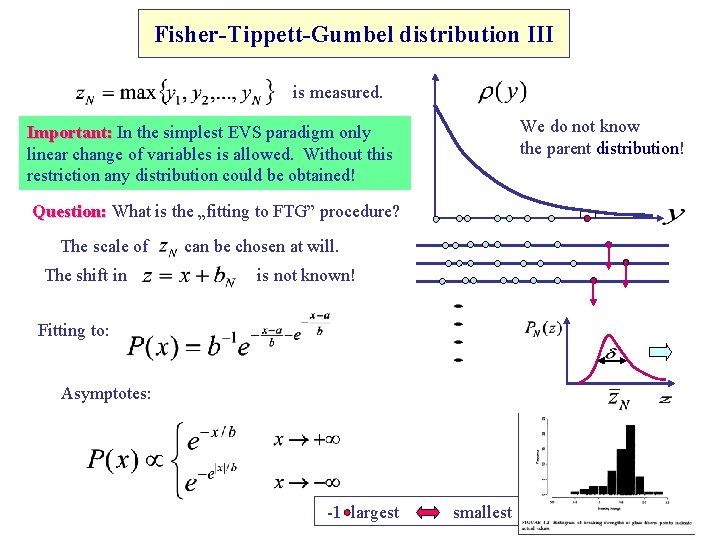
Fisher-Tippett-Gumbel distribution III is measured. We do not know the parent distribution! Important: In the simplest EVS paradigm only linear change of variables is allowed. Without this restriction any distribution could be obtained! Question: What is the „fitting to FTG” procedure? The scale of The shift in can be chosen at will. is not known! Fitting to: Asymptotes: -1 largest smallest

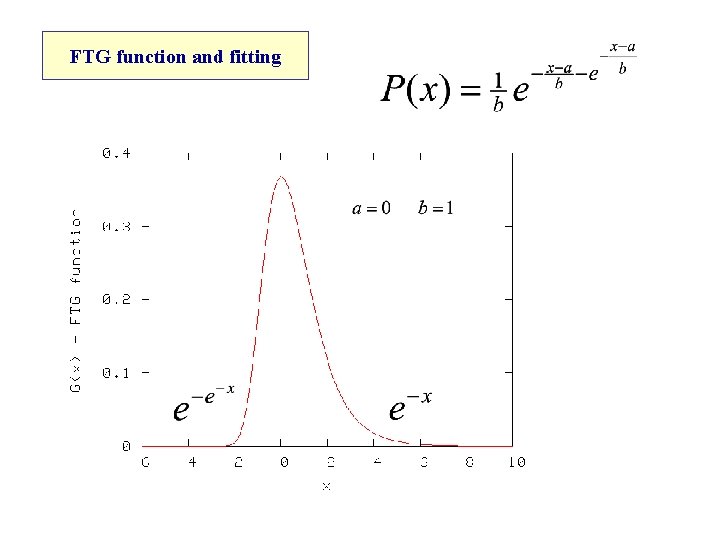
FTG function and fitting

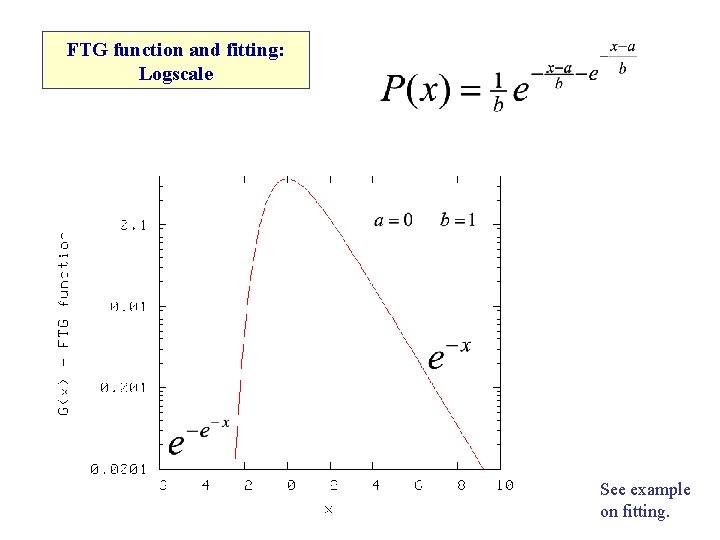
FTG function and fitting: Logscale See example on fitting.

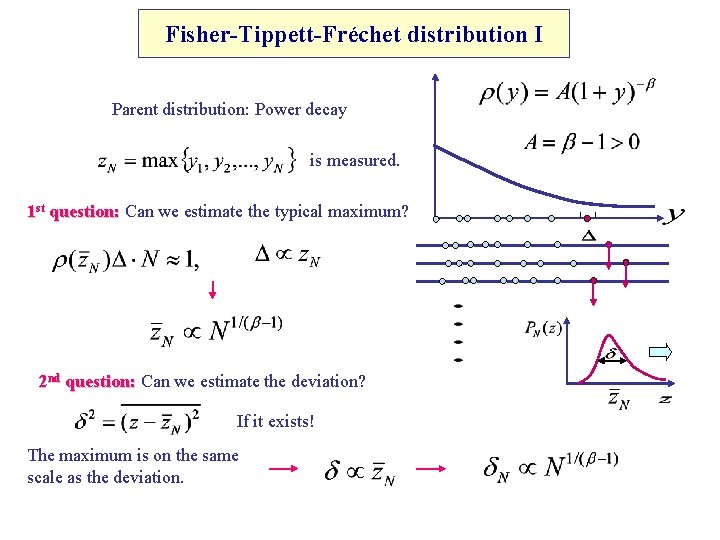
Fisher-Tippett-Fréchet distribution I Parent distribution: Power decay is measured. 1 st question: Can we estimate the typical maximum? 2 nd question: Can we estimate the deviation? If it exists! The maximum is on the same scale as the deviation.

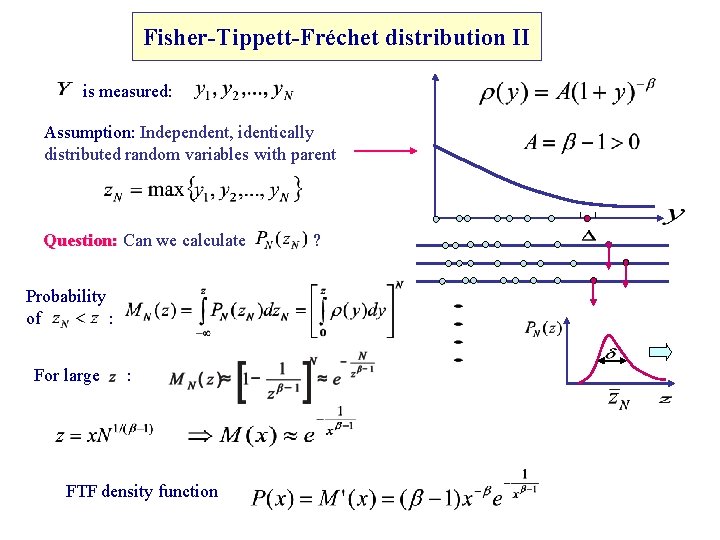
Fisher-Tippett-Fréchet distribution II is measured: Assumption: Independent, identically distributed random variables with parent Question: Can we calculate Probability of : For large : FTF density function ?

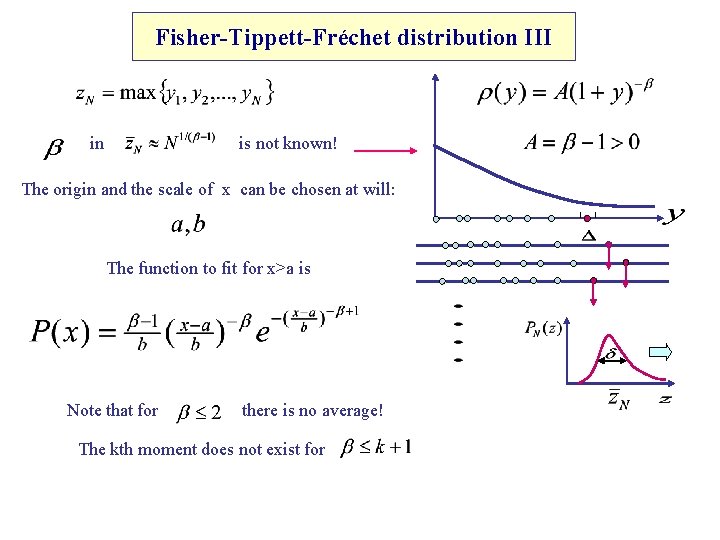
Fisher-Tippett-Fréchet distribution III in is not known! The origin and the scale of x can be chosen at will: The function to fit for x>a is Note that for there is no average! The kth moment does not exist for

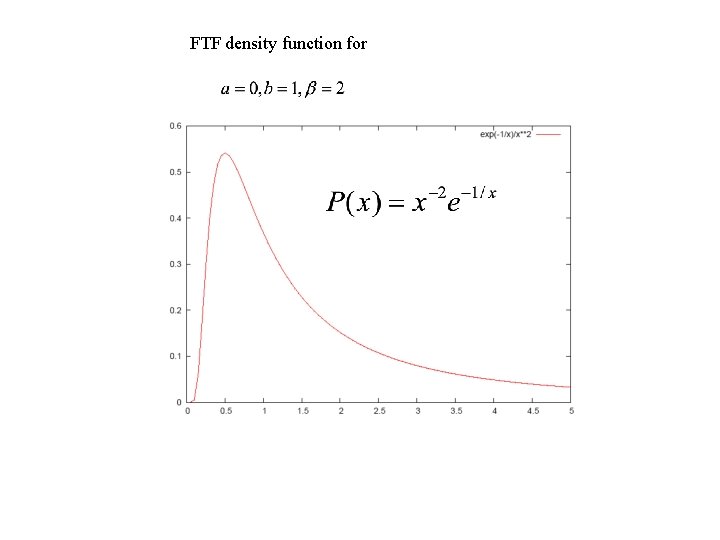
FTF density function for

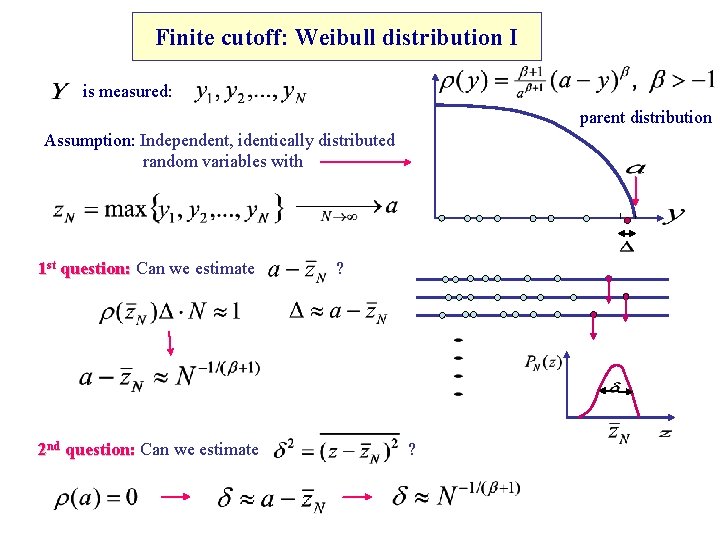
Finite cutoff: Weibull distribution I is measured: parent distribution Assumption: Independent, identically distributed random variables with 1 st question: Can we estimate 2 nd question: Can we estimate ? ?

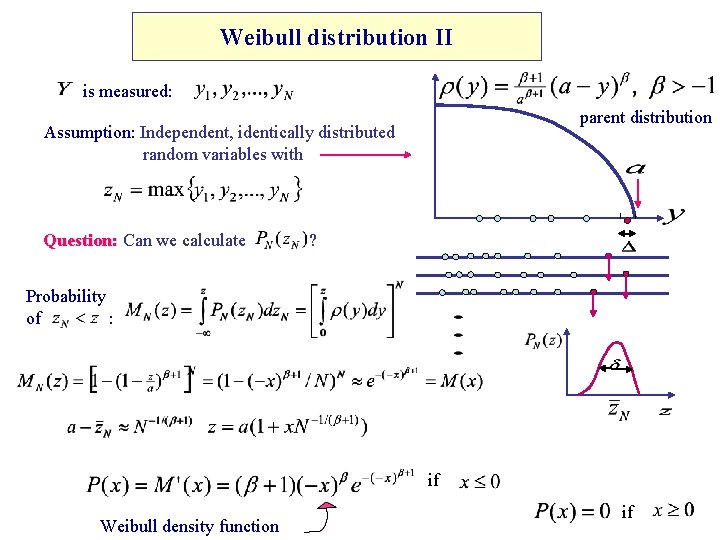
Weibull distribution II is measured: parent distribution Assumption: Independent, identically distributed random variables with Question: Can we calculate ? Probability of : if Weibull density function if

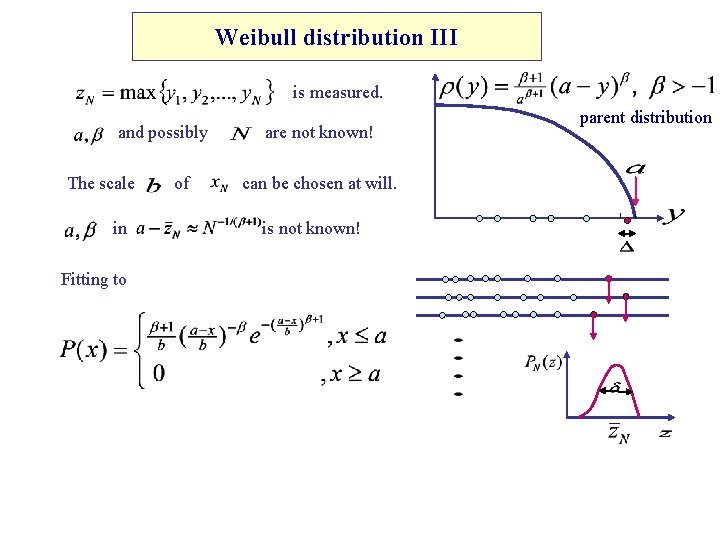
Weibull distribution III is measured. and possibly The scale in Fitting to of are not known! can be chosen at will. is not known! parent distribution

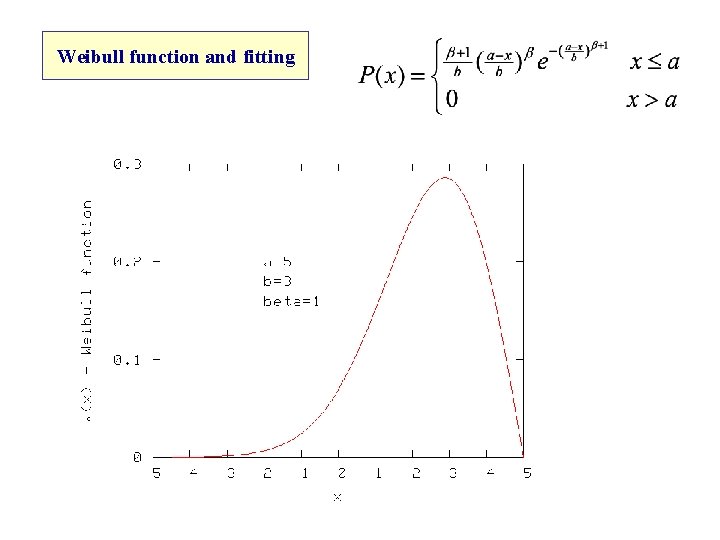
Weibull function and fitting

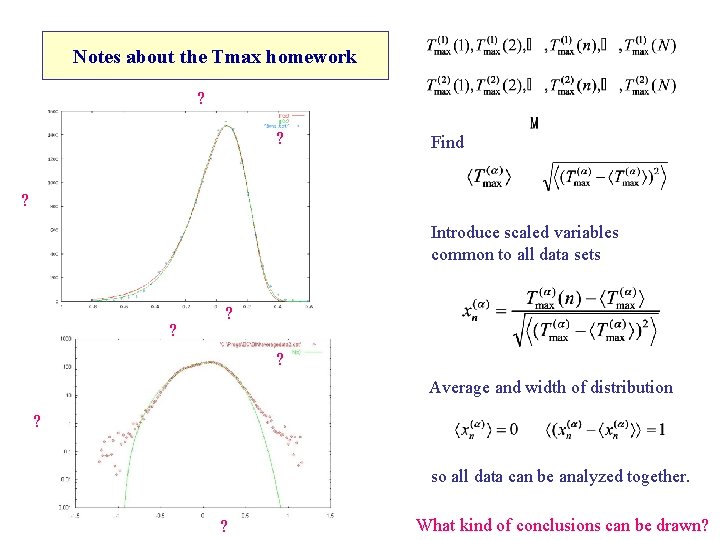
Notes about the Tmax homework ? ? Find ? Introduce scaled variables common to all data sets ? ? ? Average and width of distribution ? so all data can be analyzed together. ? What kind of conclusions can be drawn?