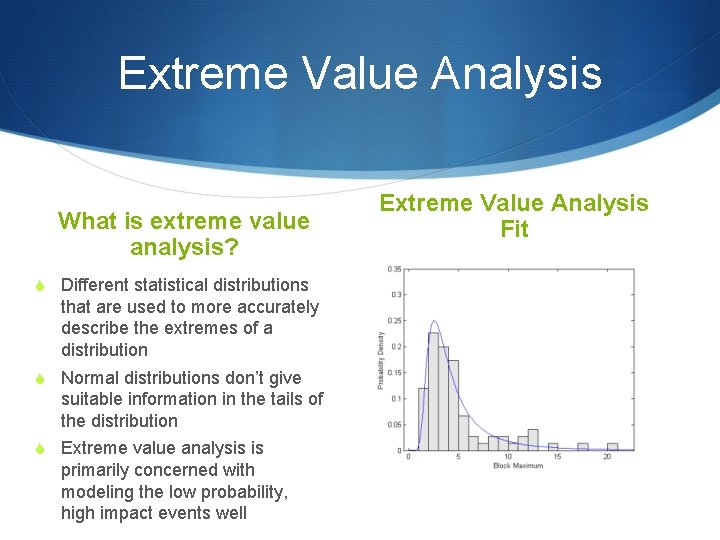
Extreme Value Analysis What is extreme value analysis

Extreme Value Analysis What is extreme value analysis? S Different statistical distributions that are used to more accurately describe the extremes of a distribution S Normal distributions don’t give suitable information in the tails of the distribution S Extreme value analysis is primarily concerned with modeling the low probability, high impact events well Extreme Value Analysis Fit

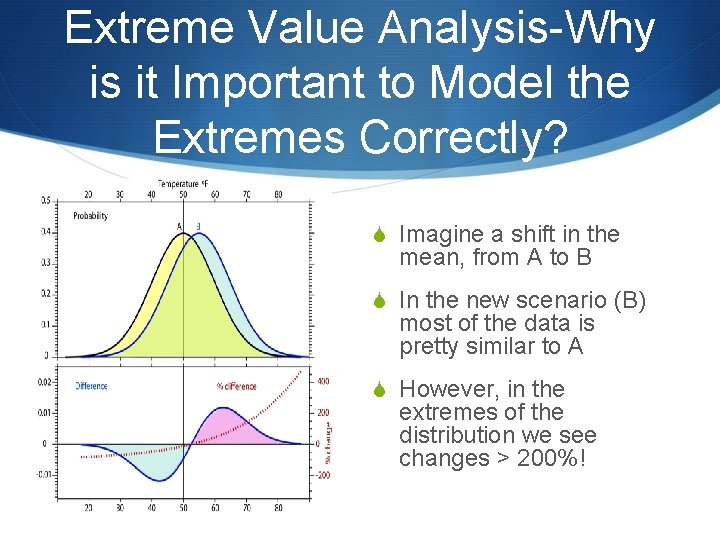
Extreme Value Analysis-Why is it Important to Model the Extremes Correctly? S Imagine a shift in the mean, from A to B S In the new scenario (B) most of the data is pretty similar to A S However, in the extremes of the distribution we see changes > 200%!

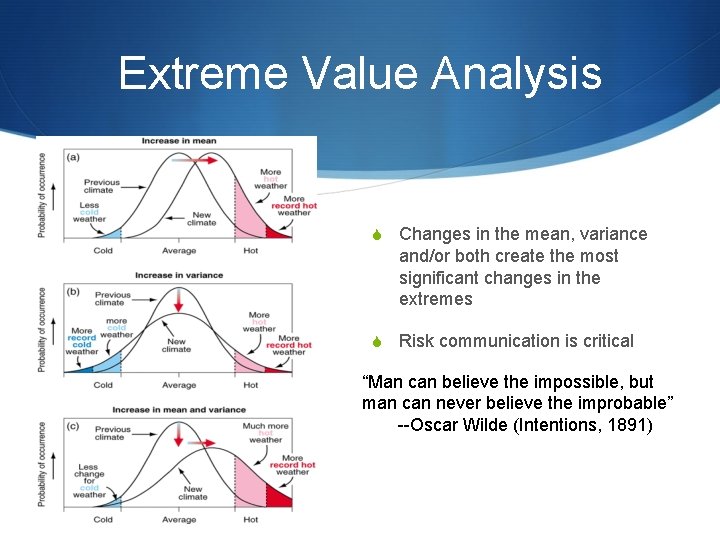
Extreme Value Analysis S Changes in the mean, variance and/or both create the most significant changes in the extremes S Risk communication is critical “Man can believe the impossible, but man can never believe the improbable” --Oscar Wilde (Intentions, 1891)

Extreme Value Analysis - Uses S Climatology S Hurricanes, heat waves, floods S Reinsurance Industry S Assessing risk of extreme events S Wall Street S Market extremes and threshold exceedence potentials S Hydrology S Floods, dam design S Water Demand!

Two Approaches To EVA Block Maxima S location parameter µ S scale parameter σ S shape parameter k S Used… S …in instances where maximums are plentiful S …when user would like to know the magnitude of an extreme event Points over Threshold S shape parameter k S scale parameter σ S threshold parameter θ S Used… S …in instances where data is limited S …when user would like to know with what frequency extreme events will occur

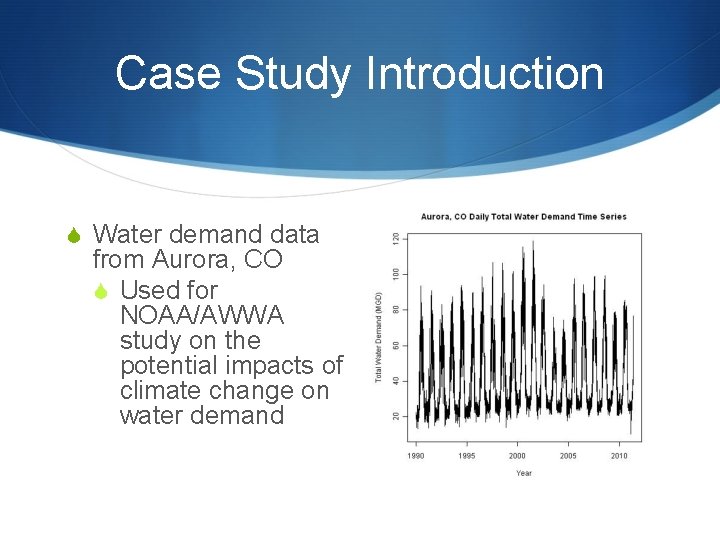
Case Study Introduction S Water demand data from Aurora, CO S Used for NOAA/AWWA study on the potential impacts of climate change on water demand

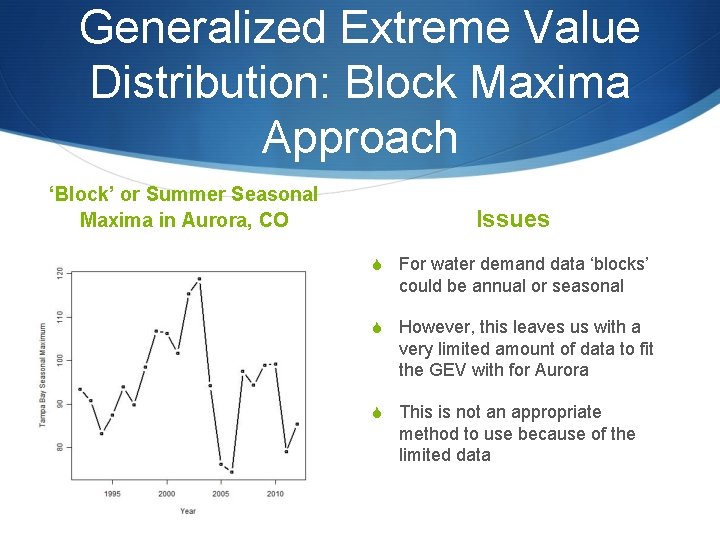
Generalized Extreme Value Distribution: Block Maxima Approach ‘Block’ or Summer Seasonal Maxima in Aurora, CO Issues S For water demand data ‘blocks’ could be annual or seasonal S However, this leaves us with a very limited amount of data to fit the GEV with for Aurora S This is not an appropriate method to use because of the limited data

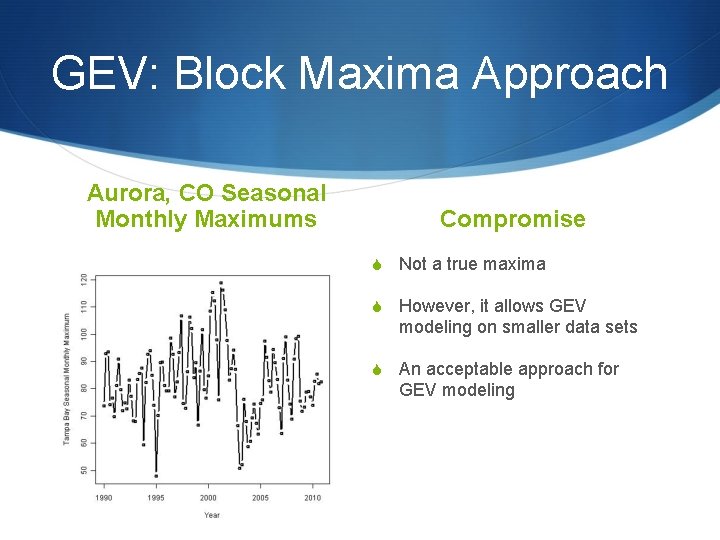
GEV: Block Maxima Approach Aurora, CO Seasonal Monthly Maximums Compromise S Not a true maxima S However, it allows GEV modeling on smaller data sets S An acceptable approach for GEV modeling

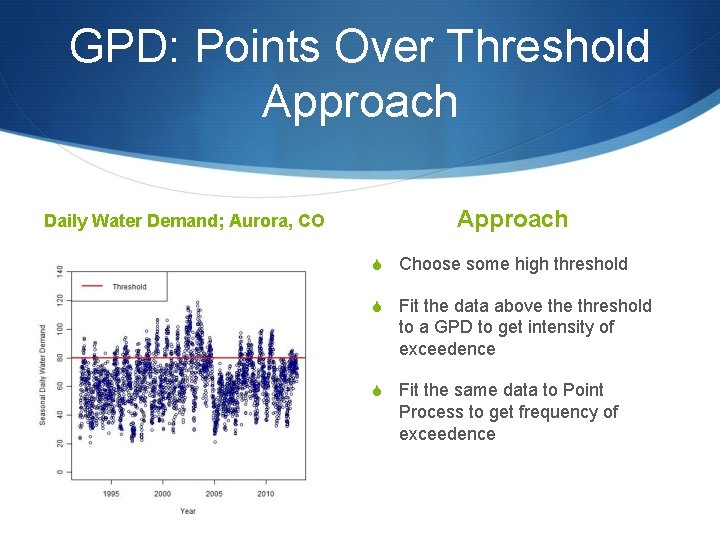
GPD: Points Over Threshold Approach Daily Water Demand; Aurora, CO Approach S Choose some high threshold S Fit the data above threshold to a GPD to get intensity of exceedence S Fit the same data to Point Process to get frequency of exceedence

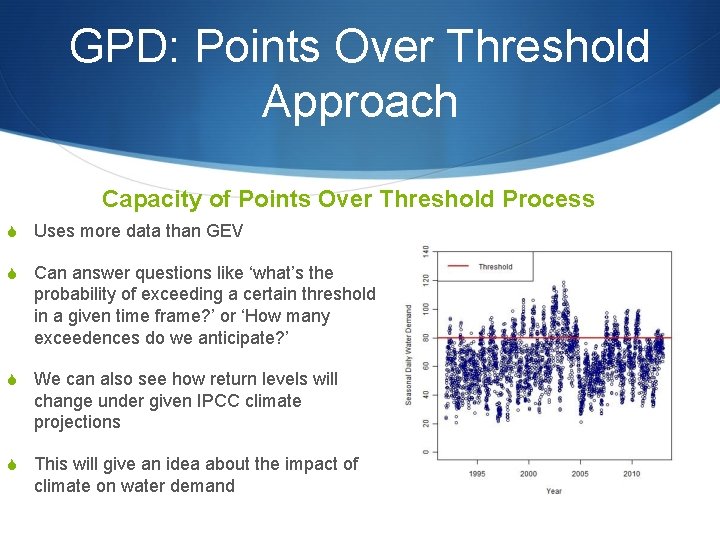
GPD: Points Over Threshold Approach Capacity of Points Over Threshold Process S Uses more data than GEV S Can answer questions like ‘what’s the probability of exceeding a certain threshold in a given time frame? ’ or ‘How many exceedences do we anticipate? ’ S We can also see how return levels will change under given IPCC climate projections S This will give an idea about the impact of climate on water demand

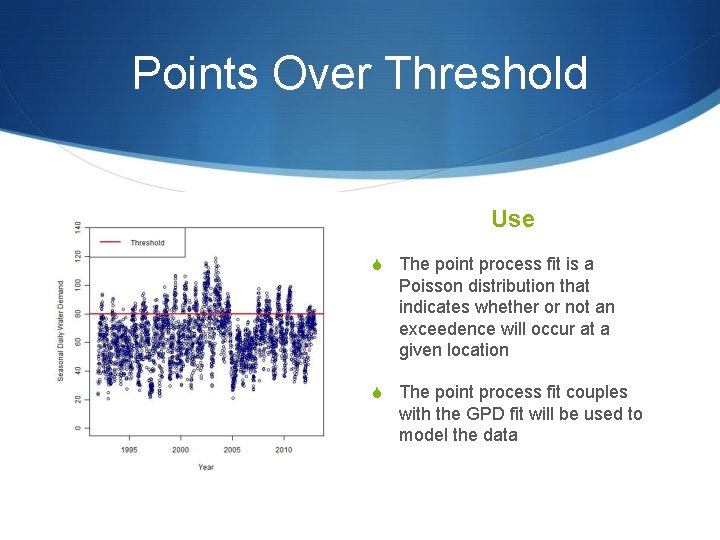
Points Over Threshold Use S The point process fit is a Poisson distribution that indicates whether or not an exceedence will occur at a given location S The point process fit couples with the GPD fit will be used to model the data

Non-Stationary EVA Benefits S Allows flexible, varying models S Improved forecasting capacity S Trends in models apparent S Potential covariates S Precipitation S Temperatures S Spell statistics S Population S Economic forecasts S etc

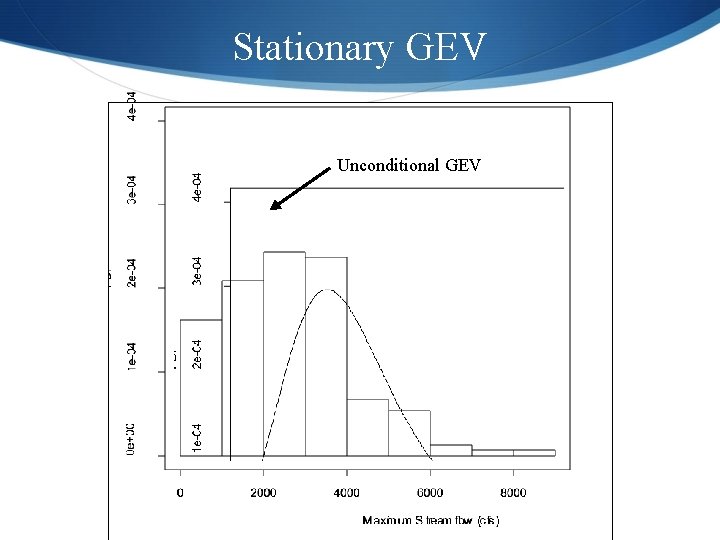
Stationary GEV Unconditional GEV

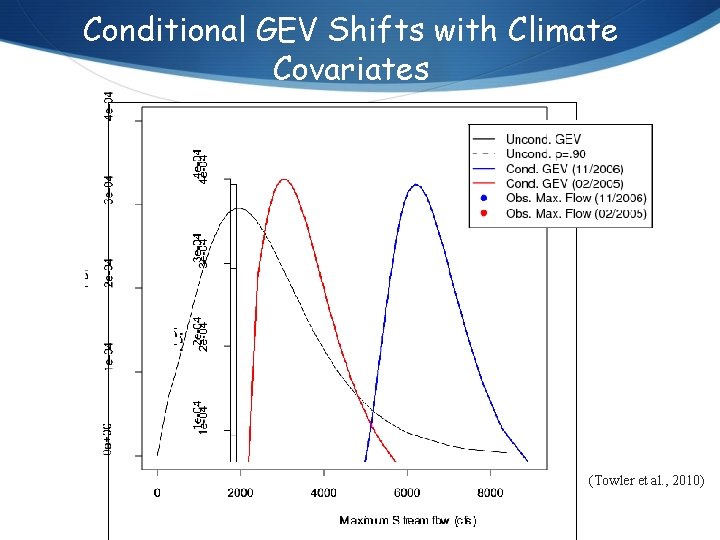
Conditional GEV Shifts with Climate Covariates (Towler et al. , 2010)

Conditional GEV Shifts with Climate Covariates Q 90 P[S>Q 90 Uncond] ? ? 40% 10% 3% (Towler et al. , 2010)

Non-Stationary Case S We can allow the extreme value parameters to vary with respect to a variety of covariates S Covariates will be the climate indicators we have been building (temp, precip, PDSI, spells, etc) S Forecasting these covariates with IPCC climate models will give the best forecast of water demand S Climate is non-stationary, water demand fluctuations with respect to climate will also not be stationary Generalized Parateo Distribution