Extremal Configurations and Levels in Pseudoline Arrangements Shakhar

Extremal Configurations and Levels in Pseudoline Arrangements Shakhar Smorodinsky (Tel-Aviv University) Joint work with Micha Sharir

What the … am I going to show/talk about? n Points are like n Lines, which are almost like n Pseudolines 2

What the … am I going to show/talk about? n So sometimes pseudolines are like points 3

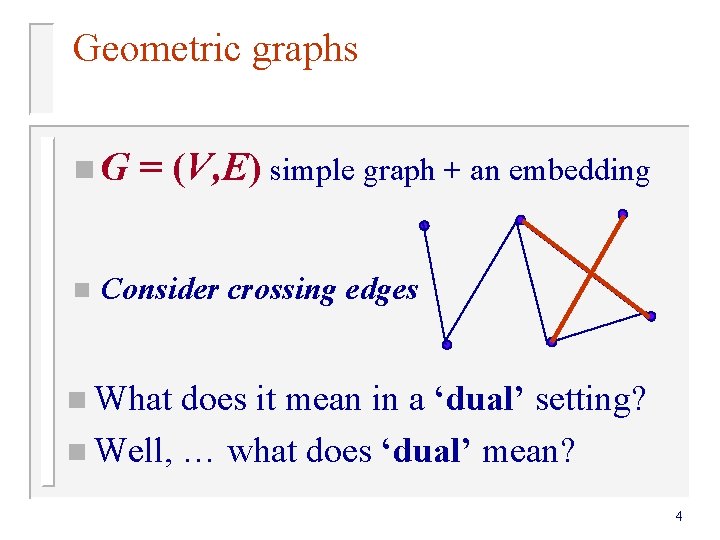
Geometric graphs n. G n = (V, E) simple graph + an embedding Consider crossing edges n What does it mean in a ‘dual’ setting? n Well, … what does ‘dual’ mean? 4

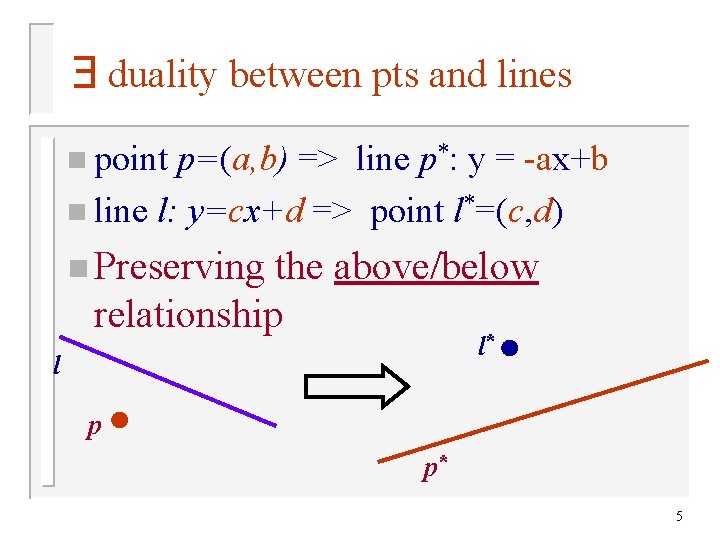
duality between pts and lines n point p=(a, b) => line p*: y = -ax+b n line l: y=cx+d => point l*=(c, d) n Preserving l the above/below relationship * l p p* 5

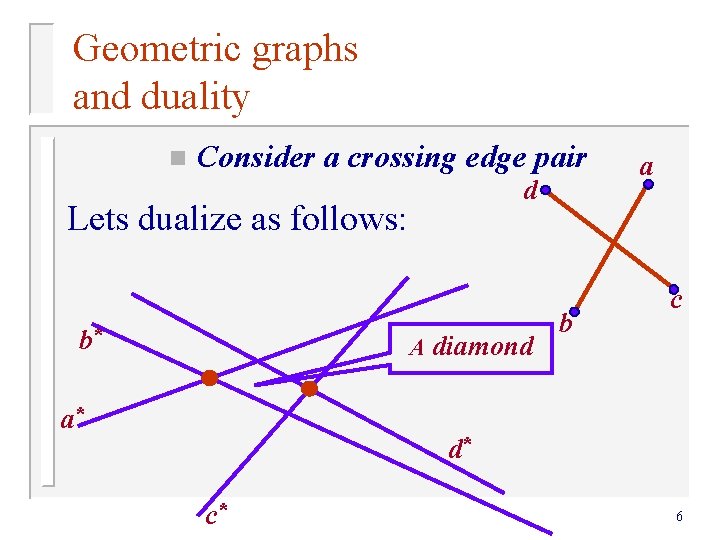
Geometric graphs and duality n Consider a crossing edge pair d Lets dualize as follows: b* A diamond a* b a c d* c* 6

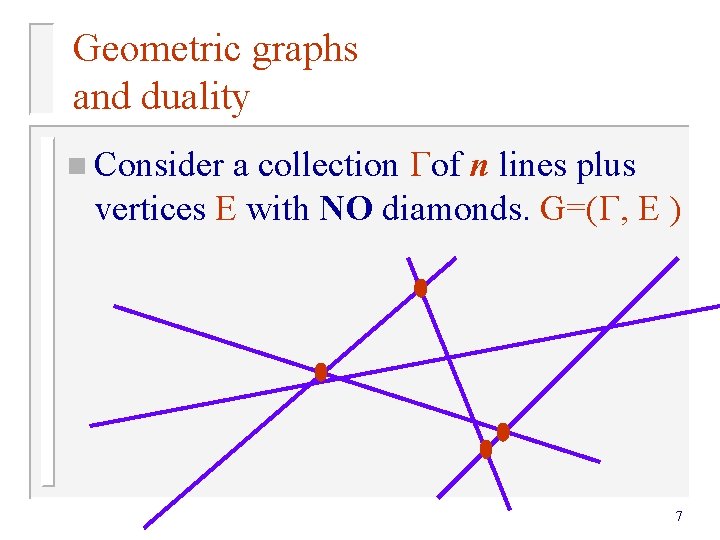
Geometric graphs and duality a collection of n lines plus vertices E with NO diamonds. G=( , E ) n Consider 7

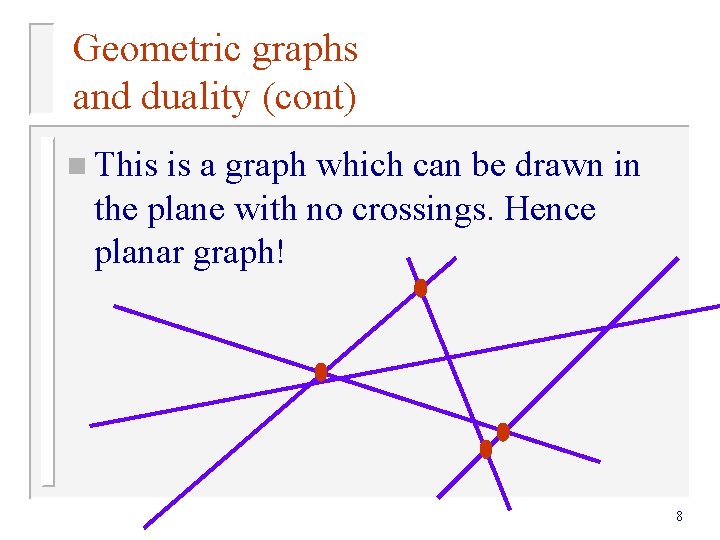
Geometric graphs and duality (cont) n This is a graph which can be drawn in the plane with no crossings. Hence planar graph! 8

Geometric graphs and duality (cont) n Does n Yes! this also hold for pseudolines? [Tamaki Tokuyama 97] 9

Geometric graphs and duality (cont) n Thm: [Tamaki Tokuyama 97] A diamond-free Pseudoline graph is planar. Proof: complicated. We provide a very simple proof. 10

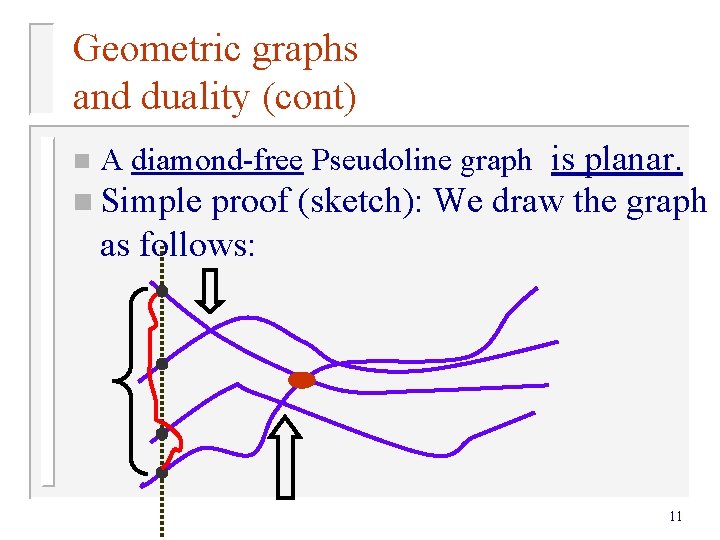
Geometric graphs and duality (cont) n A diamond-free Pseudoline graph is planar. n Simple proof (sketch): We draw the graph as follows: 11

Diamond free pseudolines graph (cont) n in this drawing any pair of edges intersect an even # times. Using Tutte [70] implies planarity 12

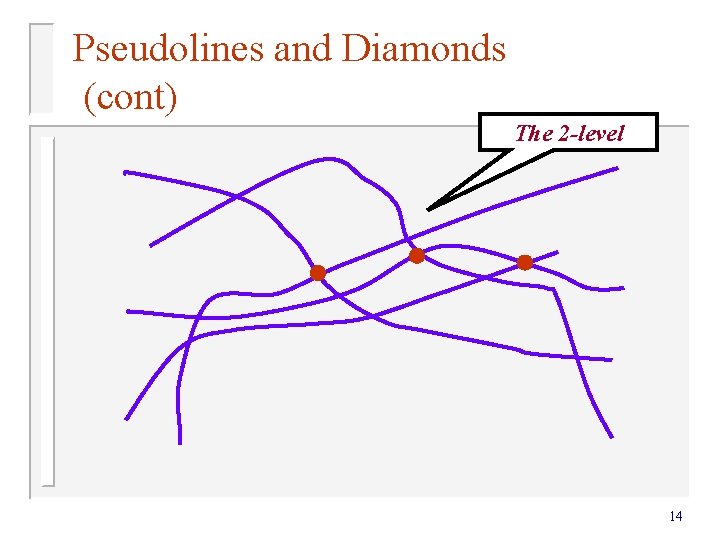
Pseudolines and Diamonds (cont) n What is diamond good for? It is an auxiliary structure that helps analyzing the complexity of the k-level. n k-level is the set of all vertices that lie above exactly k pseudolines n 13

Pseudolines and Diamonds (cont) The 2 -level 14

k-level (cont) What is the max complexity of a k-level in n (pseudo) lines? Major open problem in combinatorial geometry! Known upper bound: O(nk 1/3) [Dey 98 (for lines)] [Tamaki Tokuyama 97 (for pseudolines)] Both proofs uses the notion of diamond. 15

More on Pseudolines n We extend many results on geometric graphs to the more general case of pseudolines graphs n Example: A Thrackle is a graph drawn in the plane such that any pair of edges intersect. 16

Thrackles A Thrackle is a graph drawn in the plane such that any pair of edges intersect. n n n Conjecture (Conway): The max # edges of a Thrackle on n pts is n. Known for drawings with straight line segments. [Perles] For general drawings the best upper bound is 2 n-3 [Cairns, Nikolayevsky 2000] 17

Thrackles (cont) n We prove the conjecture for thrackles drawn with ‘extendible pseudo-segments’, by showing: n If , in a set of vertices in n pseudolines each pair form a diamond then #vertices is at most n 18

More on Pseudolines n Consider a geometric graph: n Parallel edges Thm: [Katchalski Last 98], [Valtr 98] Max # edges of geometric graph with no parallel edges is 2 n-2 n 19

Geometric graphs with no parallel edges Thm: [Katchalski Last 98], [Valtr 98] Max # edges of geometric graph with no parallel edges is 2 n-2 n 20

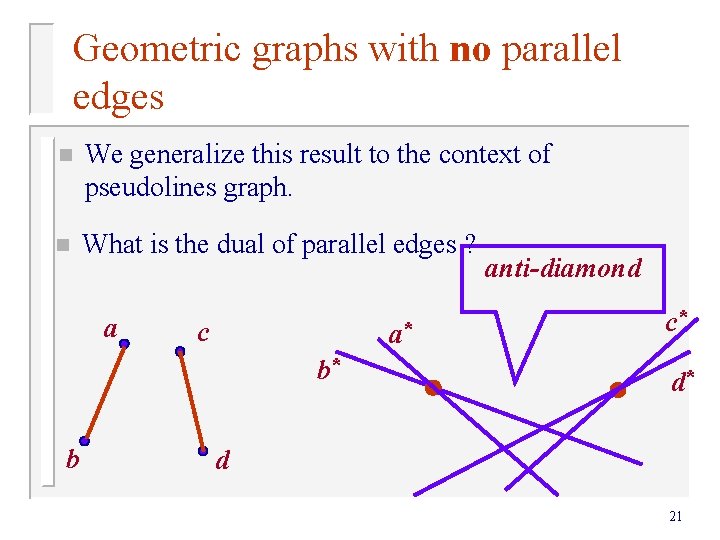
Geometric graphs with no parallel edges n We generalize this result to the context of pseudolines graph. n What is the dual of parallel edges ? a c a* b* b anti-diamond c* d* d 21

Pseudolines and anti-diamonds n Thm [S, Sharir]: An anti-diamond free pseudolines graph contains at most 2 n-2 ‘edges’ anti-diamond a* c a b* b c* d* d 22

THANK YOU Wake up!!! 23