Extrema of Functions of Two Variables using MATLAB

Extrema of Functions of Two Variables using MATLAB Isaac Bryan, Taryn Roten, Kimberly Kiser, and Kaylee Kemper

Applications � Rigid Body Dynamic � Engineering � Economics

More Applications � World Trade � Operational Research

Optimization is most commonly defined as finding the largest or smallest possible values of a function. One way to find a maximum/minimum value, is to take a derivative of the function, find all critical points, evaluate the value(s) at those points, and discover which is a maximum/minimum value by using the Fundamental Theorem of Calculus.

Using more than 2 variables � In using 2 or more variables, the concept of optimization does not change. The derivative is taken with respect to each variable brought into the function. The critical points are then found within the function from the derivatives. two variables, a critical point of a function f defined on an open set D is a point (x, y) in D where either � For ◦ At least one of fx(x, y) or fy(x, y) doesn’t exist at (x, y) ◦ fx(x, y) = fy(x, y) = 0

Using more than 2 variables (cont. ) � The discriminant of f is the expression ◦ D(x, y) = fxx(x, y) fyy(x, y) - fxy²(x, y) D(x, y) f xx(x, y) Type + + 0 + NA NA Rel. Max. Rel. Min. Saddle Point Inconclusive

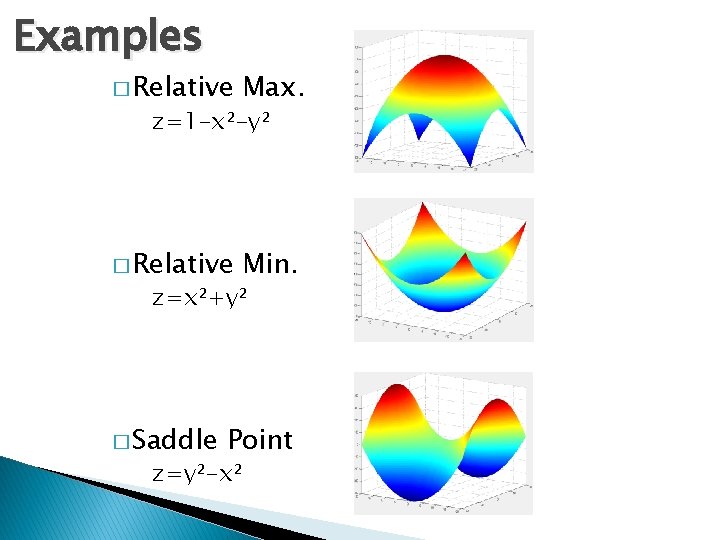
Examples � Relative Max. � Relative Min. z=1 -x²-y² z=x²+y² � Saddle Point z=y²-x²

How our Program Works � The program generates a specified number of random values to start the program � The random values are placed in a loop to approach the extrema by “walking up the gradient” � The path the program took to reach the “absolute” extremum is plotted along with the function

Testing Our Program � One Extremum z=1 -x²-y² � Relative Max. & Min. � Multiple Maxima z=9 x/(x 2+y 2+1) z=cos(x)cos(y) � Saddle Points z=y²-x²

Example of Testing Process ⇒ critical points are (-1, 0) & (1, 0)

Example of Testing Process (cont) ⇒ D(1, 0)=20. 25 ; fxx(1, 0)=-4. 5 And D(-1, 0)=20. 25 ; fxx(-1, 0)=4. 5 Therefore (1, 0, 4. 5) is a Relative Maximum And (-1, 0, -4. 5) is a Relative Minimum

Issues with the Technique � Existence � Multiple � Global of a maximum maxima Maximum vs. Relative Maximum

Goals for Next Semester � Multiple Variables � Fewer Test Points � Faster Process

Cool Functions