Extrapolation of trialbased survival curves constraints based on

Extrapolation of trial-based survival curves: constraints based on external information Patricia Guyot 1, 2, Nicky J Welton 1, AE Ades 1 Thanks to: M Beasley 3 1 School of Social and Community Medicine, University of Bristol 2 Mapi Consultancy 3 Bristol Haematology and Oncology Centre BAYES 2014, University College London, London 11 th- 13 th June 2014

Why Extrapolate Survival Curves? • Health Technology Assessment requires a comparison of the expected quality-adjusted life-years between different technologies • A key element is difference in life expectancy • End-Of-Life criterion also require estimates of: • life expectancy • gains in life expectancy

Life Expectancy Difference • Difference in mean survival times • Can be calculated as the difference in areas between the curves over lifetime • But trials typically follow-up for just a few years • Mean survival times very sensitive to assumptions on what happens after the trial follow-up (in the “tails” of the curves)

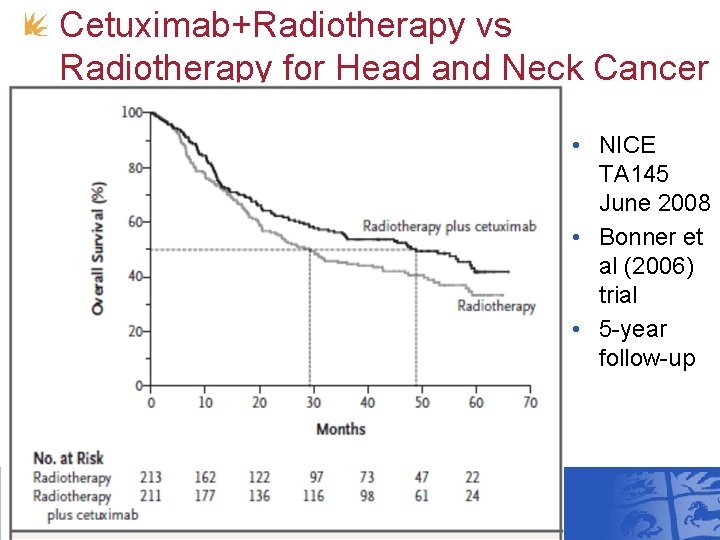
Cetuximab+Radiotherapy vs Radiotherapy for Head and Neck Cancer • NICE TA 145 June 2008 • Bonner et al (2006) trial • 5 -year follow-up

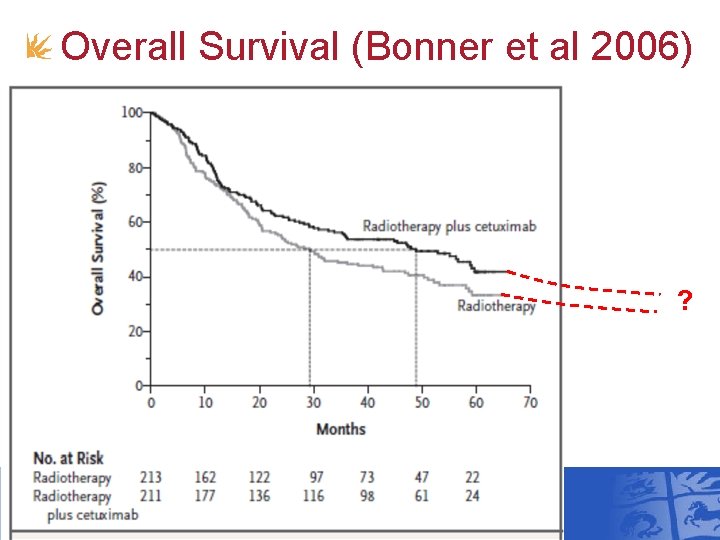
Overall Survival (Bonner et al 2006) ?

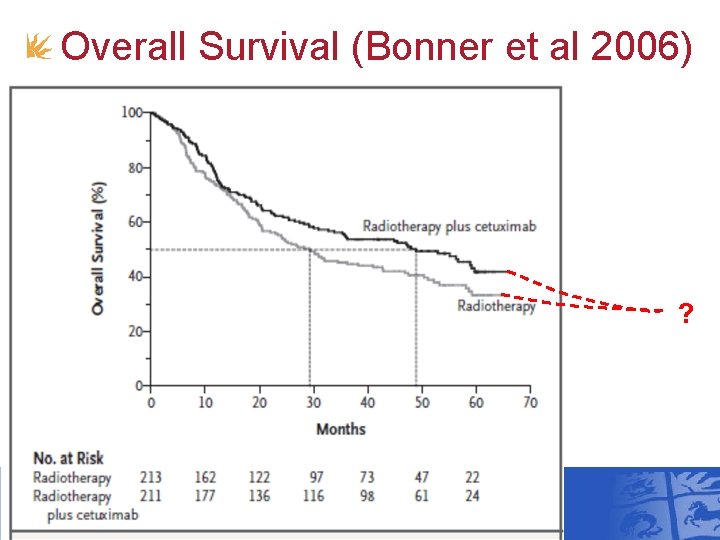
Overall Survival (Bonner et al 2006) ?

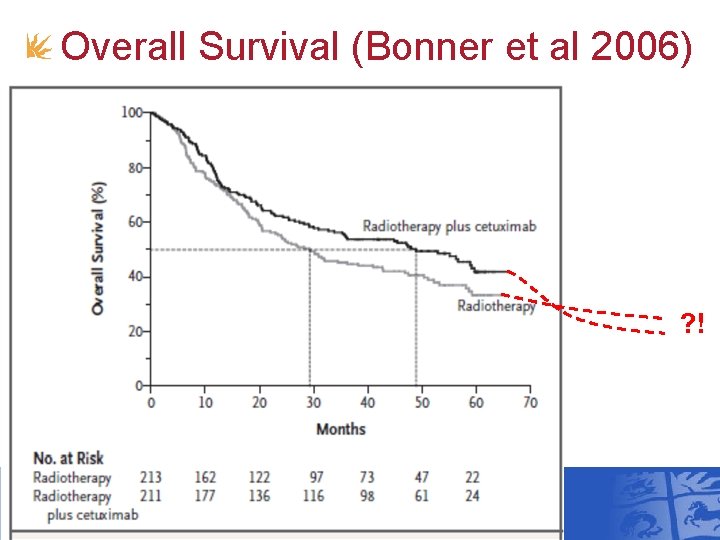
Overall Survival (Bonner et al 2006) ? !

How to Extrapolate? • Need to assume something about: • the survival time distribution • Eg: Exponential, Weibull, Log-Normal. . . • Cox models don’t help with this • the hazard ratio • proportional hazards (constant hazard ratio) • increasing or decreasing hazard ratio • “bath-tub” hazard ratio • Helps to have individual patient data, or sufficient statistics to explore alternative curves

Recontructing data from published Kaplan-Meier curves • Guyot et al. (2012) method to approximate the data used to produce kaplan-meier curves • Inputs: • Uses software to obtain co-ordinates from image from a. pdf file (we used digitizeit) • Numbers at risk published below the curve (defines fixed number of intervals) • Total number of deaths/events (if reported)

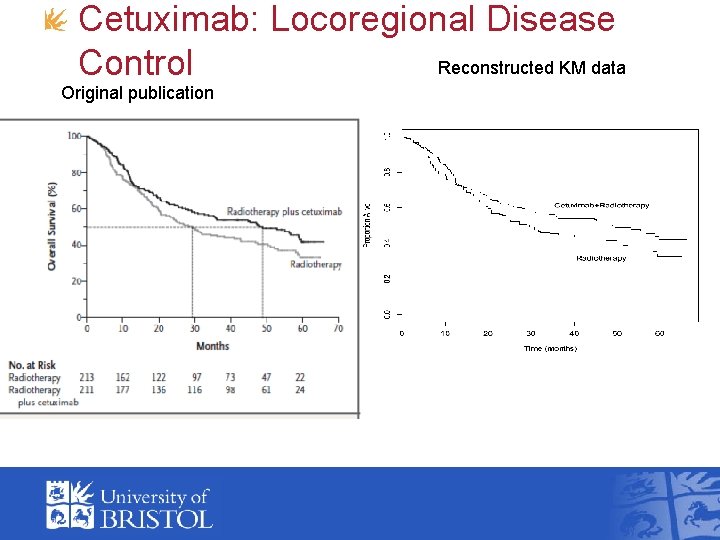
Cetuximab: Locoregional Disease Reconstructed KM data Control Original publication

Cetuximab Reconstruction Results Original publication Reconstructed KM data 2 -year survival (%) 55 55 (49, 63) 3 -year survival (%) 45 45 (39, 52) 29. 3 29. 6 (22. 6, 43. 0) survival rate (2 years) 62 62 (55, 69) survival rate (3 years) 55 55 (48, 62) 49. 0 48. 9 (34. 2, NA) 0. 74 (0. 57, 0. 97) 0. 77 (0. 59, 0. 996) Radiotherapy arm median survival (months) Radiotherapy plus cetuximab arm median duration Hazard ratio with 95%CI

Back to Extrapolation. . . • Using reconstructed data we can estimate a variety of different survival models. . .

Exponential Extrapolation (poor fit) 100 90 Mean survival difference: 17 mths (2. 1, 33. 45) 80 overall survival (%) 70 60 50 40 30 20 10 0 0 5 10 15 20 Years 25 30 35 40

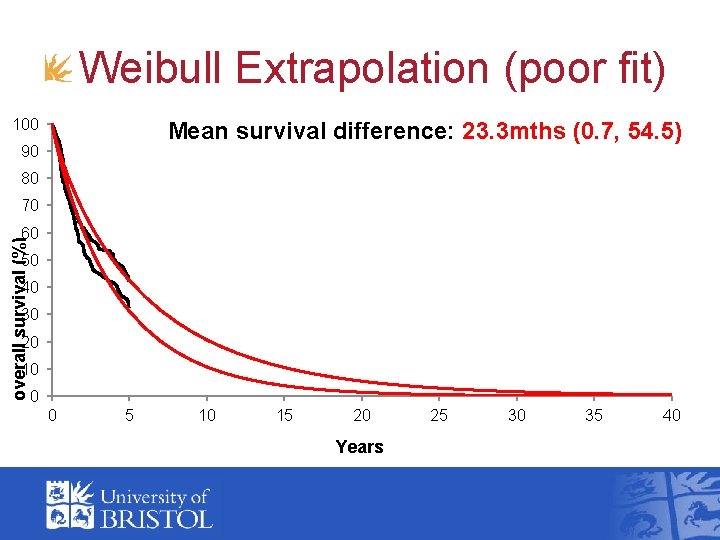
Weibull Extrapolation (poor fit) 100 Mean survival difference: 23. 3 mths (0. 7, 54. 5) 90 80 70 overall survival (%) 60 50 40 30 20 10 0 0 5 10 15 20 Years 25 30 35 40

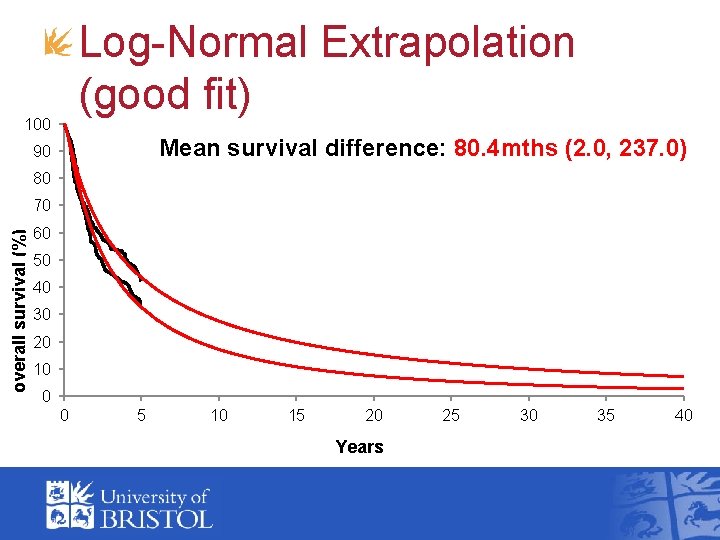
Log-Normal Extrapolation (good fit) 100 Mean survival difference: 80. 4 mths (2. 0, 237. 0) 90 80 overall survival (%) 70 60 50 40 30 20 10 0 0 5 10 15 20 Years 25 30 35 40

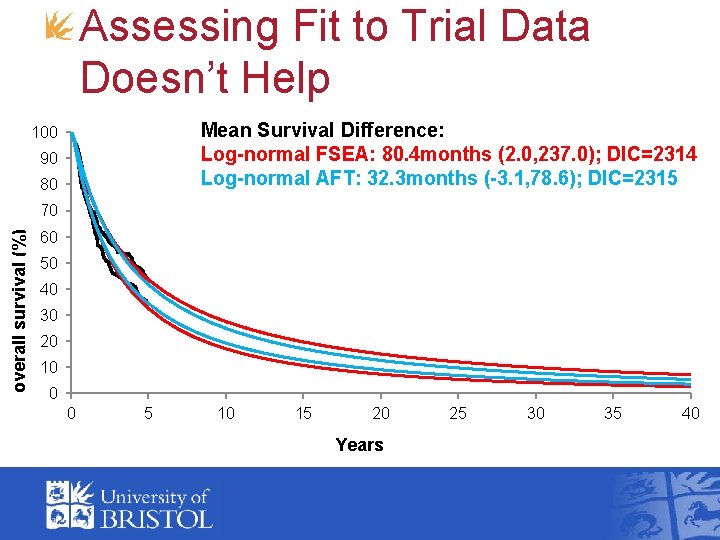
Assessing Fit to Trial Data Doesn’t Help Mean Survival Difference: Log-normal FSEA: 80. 4 months (2. 0, 237. 0); DIC=2314 Log-normal AFT: 32. 3 months (-3. 1, 78. 6); DIC=2315 100 90 80 overall survival (%) 70 60 50 40 30 20 10 0 0 5 10 15 20 Years 25 30 35 40

Possible Solution: Use External Data To Inform Extrapolation • Observational evidence e. g. • General population • Registry (e. g. Surveillance Epidemiology and End Results) • Other RCT evidence e. g. • Meta-analyses (e. g. Pignon et al. 2009) • longer RCTs • Expert opinion

Estimation • Model RCT and external data simultaneously with linked parameters • Bayesian approach • Eg constraint that general population overall survival better than that in Bonner control arm • Linking function: • Prior:

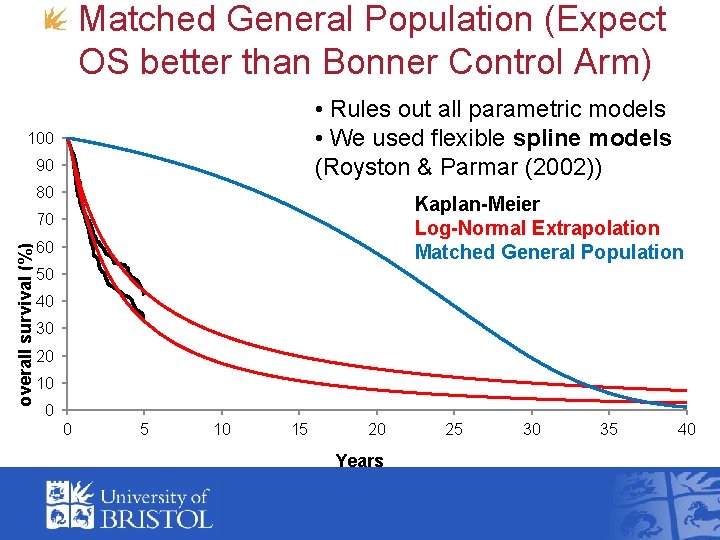
Matched General Population (Expect OS better than Bonner Control Arm) • Rules out all parametric models • We used flexible spline models (Royston & Parmar (2002)) 100 90 80 Kaplan-Meier Log-Normal Extrapolation Matched General Population overall survival (%) 70 60 50 40 30 20 10 0 0 5 10 15 20 Years 25 30 35 40

Expert view on Bonner trial • In H&N, relapse is high for first 2 years, and then declines • Effect of cetuximab is to increase the proportion of cells sensitive to radiotherapy and so lower the risk of relapse • Duration of treatment effect should be the same as the time interval over which the relapses occur • Those who die of H&N cancer tend to die in first 5 years • Conditional survival in both arms should “stabilize” and converge after 5 years (i. e. HR tends to 1)

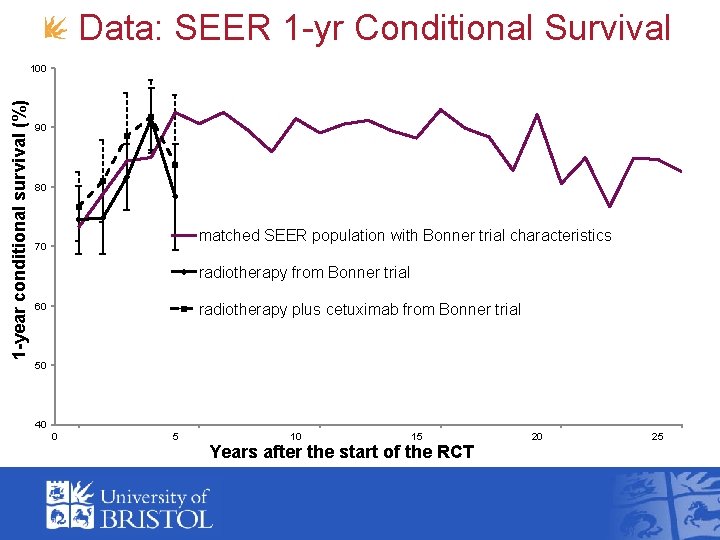
Data: SEER 1 -yr Conditional Survival 1 -year conditional survival (%) 100 90 80 matched SEER population with Bonner trial characteristics 70 radiotherapy from Bonner trial radiotherapy plus cetuximab from Bonner trial 60 50 40 0 5 10 15 Years after the start of the RCT 20 25

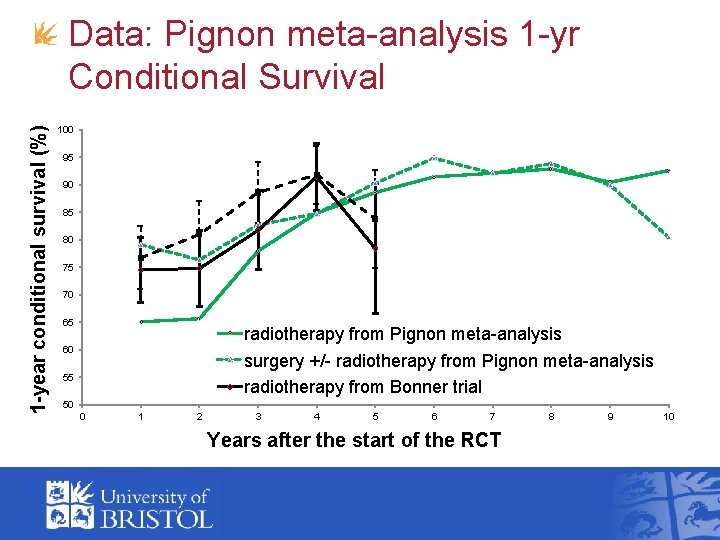
1 -year conditional survival (%) Data: Pignon meta-analysis 1 -yr Conditional Survival 100 95 90 85 80 75 70 65 radiotherapy from Pignon meta-analysis surgery +/- radiotherapy from Pignon meta-analysis radiotherapy from Bonner trial 60 55 50 0 1 2 3 4 5 6 7 Years after the start of the RCT 8 9 10

All Constraints • Control arm overall survival less than matched UK general population • 1 -year conditional survival in control arm is no different to that in SEER database • Hazard ratio tends to 1 as time from treatment increases

Implementation: Gen Pop Survival • Likelihood for the external data: Ø r: number alive at time T; n: number at risk at time 0 • Linking function Ø Overall survival , e. g. • Prior: Ø Constrain general population survival to be better than that for advanced head and neck cancer patients

Implementation: SEER 1 -year Conditional Survival • Belief that 1 -year conditional survival on radiotherapy equal to that from SEER • Linking functions Ø Binomial likelihood (each time-point conditionally independent) Ø 1 -year Conditional survival on control arm

Implementation: HR tends to 1 • Belief that HR tends to 1 • Likelihood for the external data Ø Normal for external HR • Linking functions Ø Normal likelihood for hazard ratios: Ø Hazard ratio of treatment vs. control

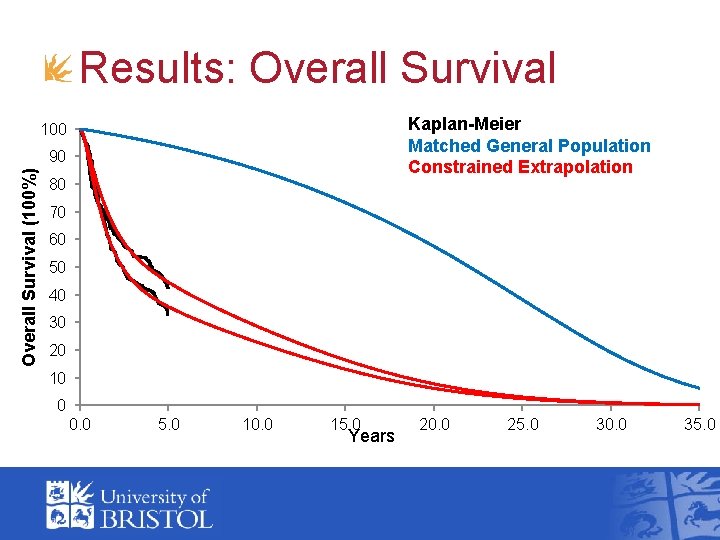
Results: Overall Survival Kaplan-Meier Matched General Population Constrained Extrapolation 100 Overall Survival (100%) 90 80 70 60 50 40 30 20 10 0 0. 0 5. 0 10. 0 15. 0 Years 20. 0 25. 0 30. 0 35. 0

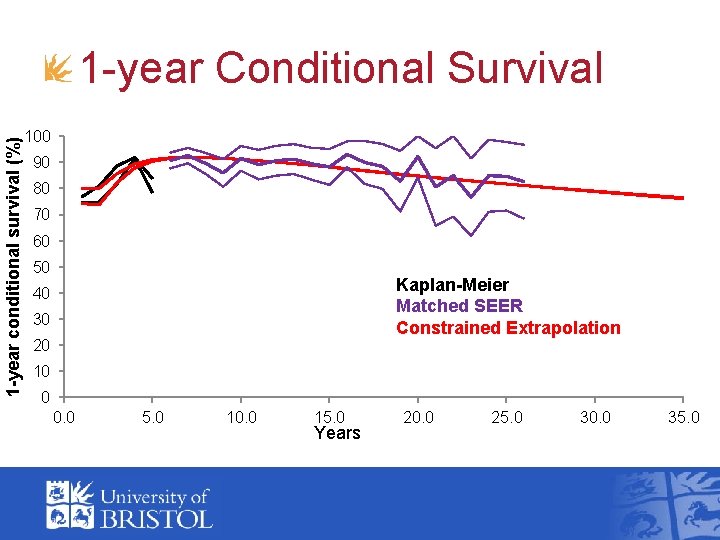
1 -year conditional survival (%) 1 -year Conditional Survival 100 90 80 70 60 50 Kaplan-Meier Matched SEER Constrained Extrapolation 40 30 20 10 0 0. 0 5. 0 10. 0 15. 0 Years 20. 0 25. 0 30. 0 35. 0

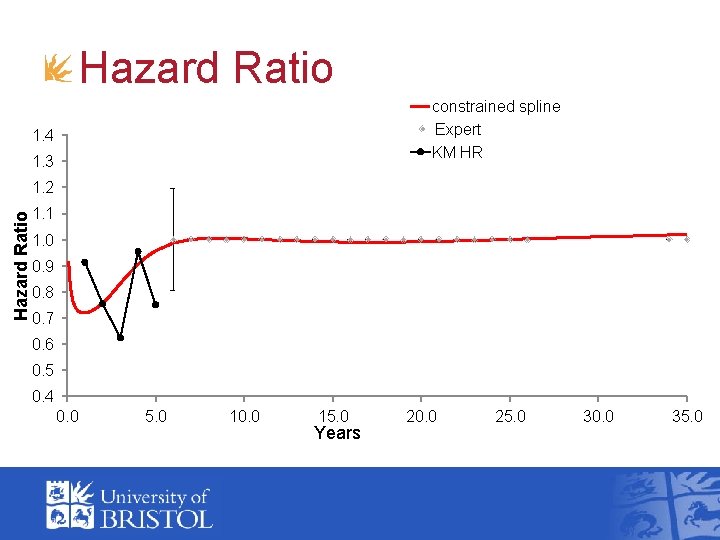
Hazard Ratio constrained spline Expert KM HR 1. 4 1. 3 Hazard Ratio 1. 2 1. 1 1. 0 0. 9 0. 8 0. 7 0. 6 0. 5 0. 4 0. 0 5. 0 10. 0 15. 0 Years 20. 0 25. 0 30. 0 35. 0

Overall Survival Difference in life expectancy: 5 months [95%Cr. L: 0; 9] 100 Overall Survival (100%) 90 80 Kaplan-Meier radiotherapy arm 70 60 constrained spline radiotherapy arm 50 40 30 20 10 0 0. 0 5. 0 10. 0 15. 0 Years 20. 0 25. 0 30. 0 35. 0

Discussion • Spline models tricky to estimate • Possible alternative flexible models include fractional polynomials, mixture models • Relies on identification of relevant external evidence sources • Clinical input essential to help identify relevant sources

References • Bonner et al. 2006. NEJM 354: 567 -78 • Pignon JP et al. 2009. Radiotherapy and Oncology 92: 4 -14 • Surveillance, Epidemiology, and End Results (SEER) Database (www. seer. cancer. gov) • Guyot P, Welton NJ, Ades AE. Enhanced secondary analysis of survival data: reconstructing the data from published Kaplan -Meier survival curves. BMC Medical Research Methodology 2012. 12: 9 • Royston P, Parmar MK. 2002. Stats in Med 21: 2175 -2197