Extracting Functions from Boolean Relations Jordi Cortadella Universitat

Extracting Functions from Boolean Relations Jordi Cortadella Universitat Politècnica de Catalunya

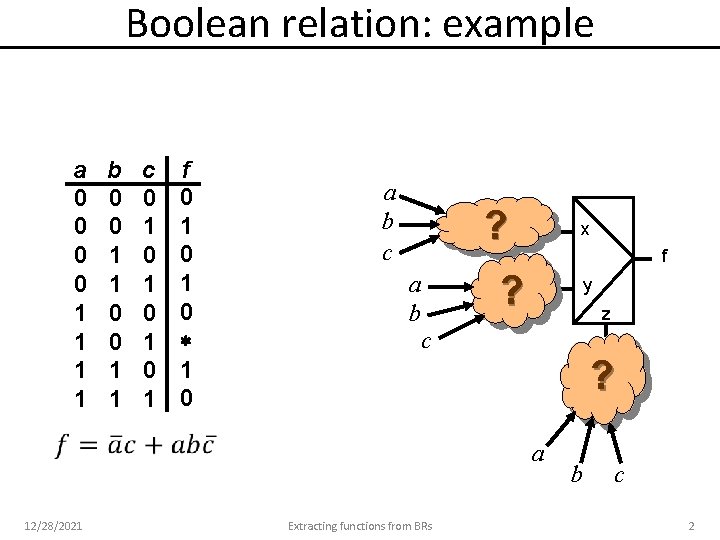
Boolean relation: example a 0 0 1 1 b 0 0 1 1 c 0 1 0 1 f 0 1 0 a b c ? a b c x f ? y z ? a 12/28/2021 Extracting functions from BRs b c 2

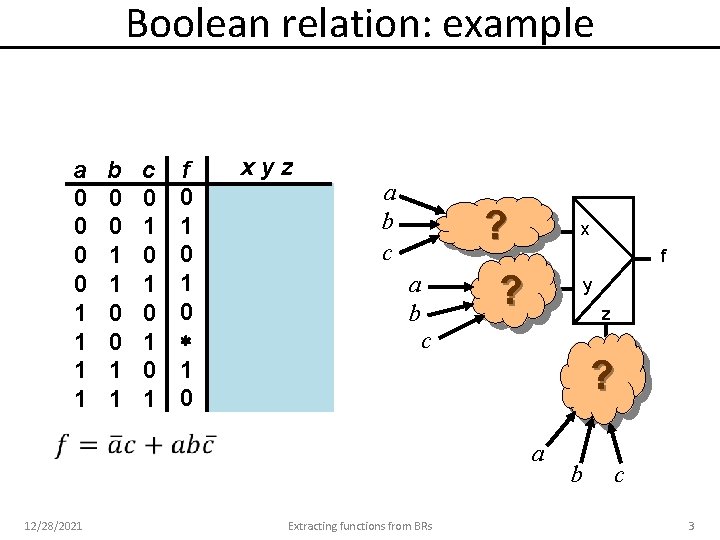
Boolean relation: example a 0 0 1 1 b 0 0 1 1 c 0 1 0 1 f 0 1 0 xyz a b c ? a b c x f ? y z ? a 12/28/2021 Extracting functions from BRs b c 3

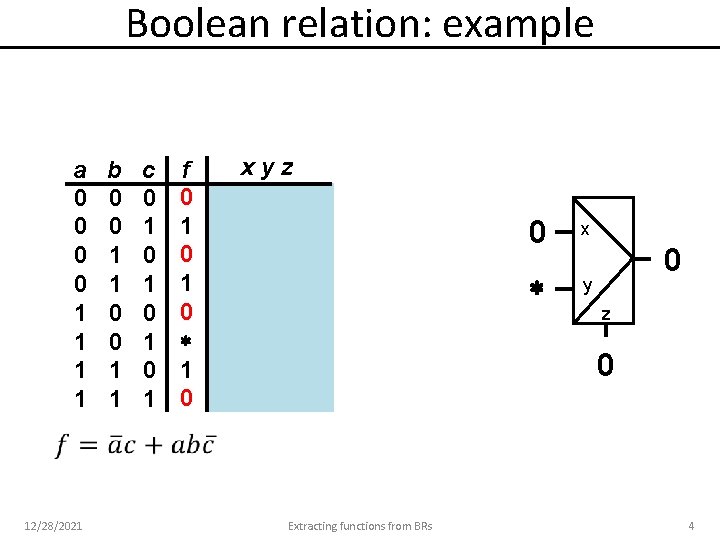
Boolean relation: example a 0 0 1 1 12/28/2021 b 0 0 1 1 c 0 1 0 1 f 0 1 0 xyz 0 x y 0 z 0 Extracting functions from BRs 4

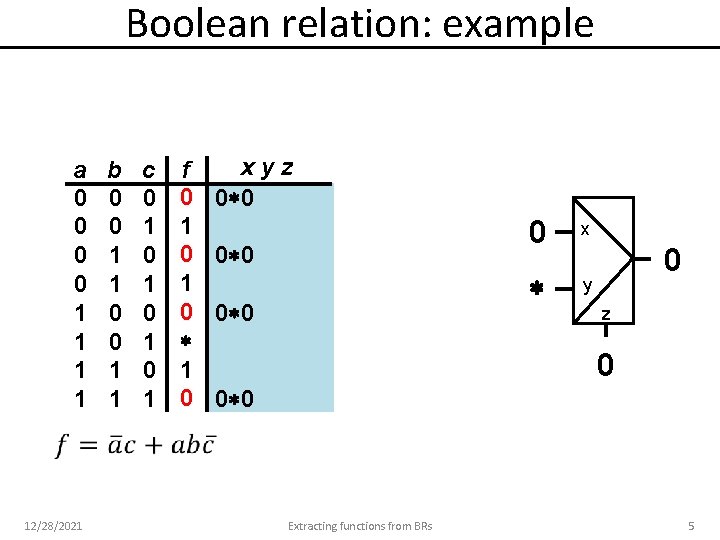
Boolean relation: example a 0 0 1 1 12/28/2021 b 0 0 1 1 c 0 1 0 1 f 0 1 0 xyz 0 0 0 0 x y 0 z 0 0 0 Extracting functions from BRs 5

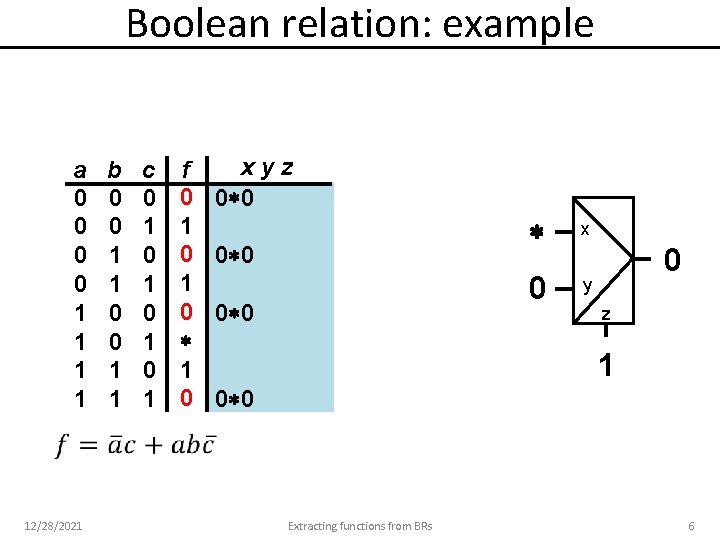
Boolean relation: example a 0 0 1 1 12/28/2021 b 0 0 1 1 c 0 1 0 1 f 0 1 0 xyz 0 0 0 x 0 y 0 z 1 0 0 Extracting functions from BRs 6

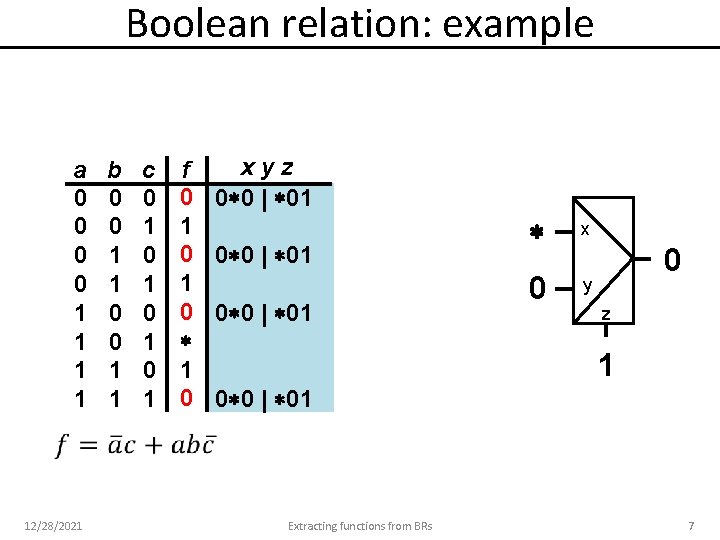
Boolean relation: example a 0 0 1 1 12/28/2021 b 0 0 1 1 c 0 1 0 1 f 0 1 0 xyz 0 0 | 01 x 0 y 0 z 1 0 0 | 01 Extracting functions from BRs 7

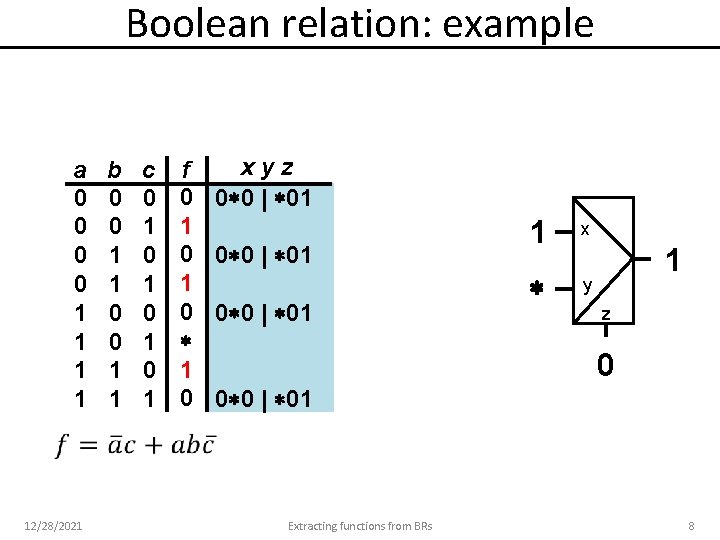
Boolean relation: example a 0 0 1 1 12/28/2021 b 0 0 1 1 c 0 1 0 1 f 0 1 0 xyz 0 0 | 01 1 x y 1 z 0 0 0 | 01 Extracting functions from BRs 8

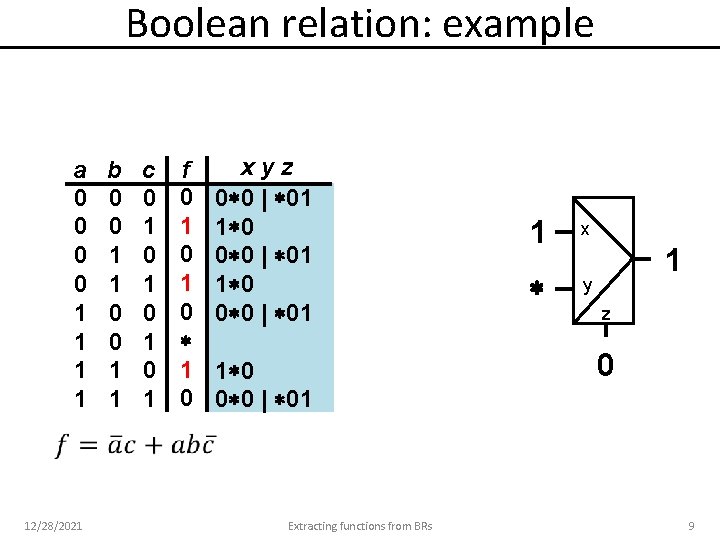
Boolean relation: example a 0 0 1 1 12/28/2021 b 0 0 1 1 c 0 1 0 1 f 0 1 0 xyz 0 0 | 01 1 0 0 0 | 01 Extracting functions from BRs 1 x y 1 z 0 9

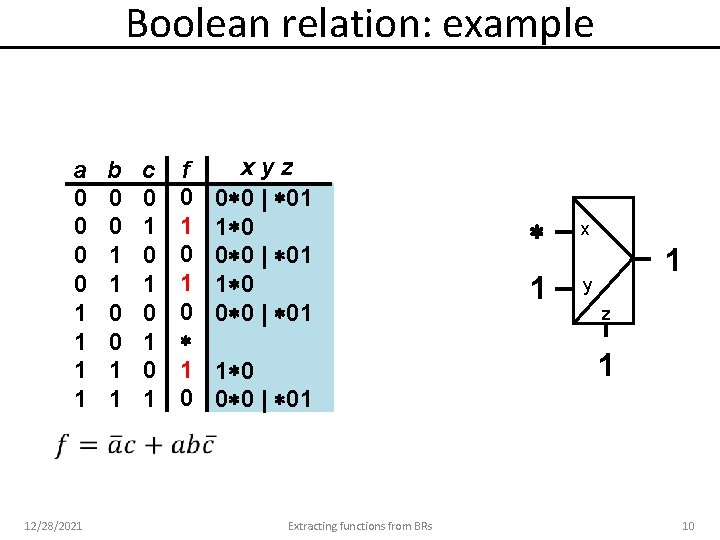
Boolean relation: example a 0 0 1 1 12/28/2021 b 0 0 1 1 c 0 1 0 1 f 0 1 0 xyz 0 0 | 01 1 0 0 0 | 01 Extracting functions from BRs x 1 y 1 z 1 10

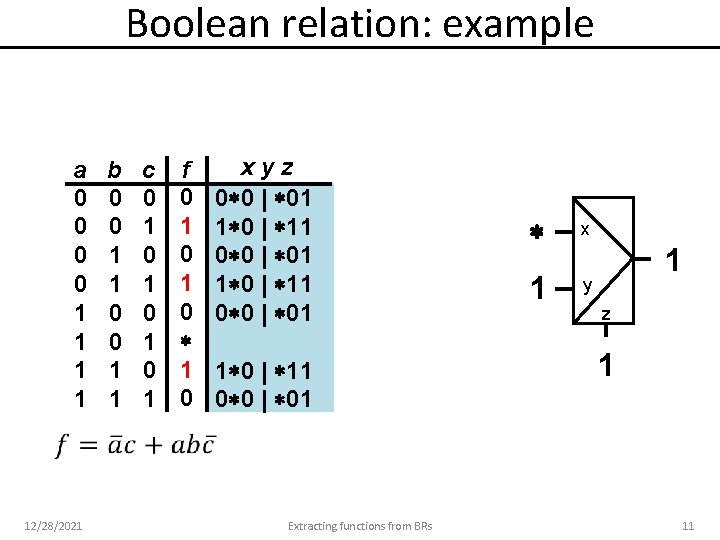
Boolean relation: example a 0 0 1 1 12/28/2021 b 0 0 1 1 c 0 1 0 1 f 0 1 0 xyz 0 0 | 01 1 0 | 11 0 0 | 01 Extracting functions from BRs x 1 y 1 z 1 11

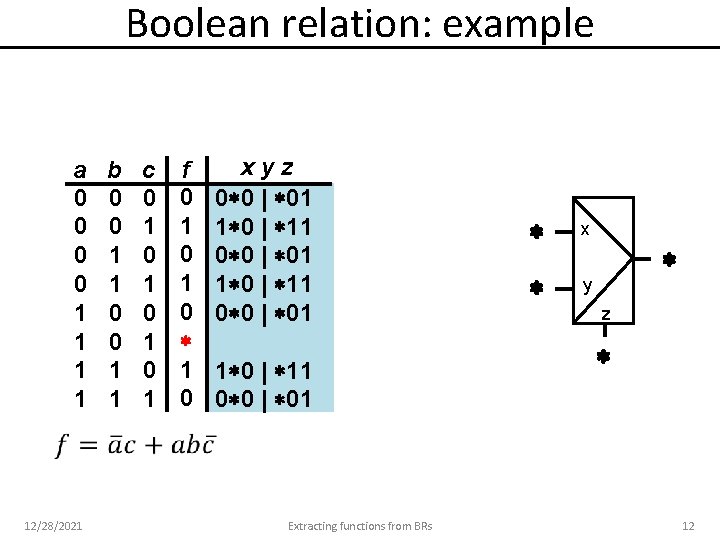
Boolean relation: example a 0 0 1 1 12/28/2021 b 0 0 1 1 c 0 1 0 1 f 0 1 0 xyz 0 0 | 01 1 0 | 11 0 0 | 01 Extracting functions from BRs x y z 12

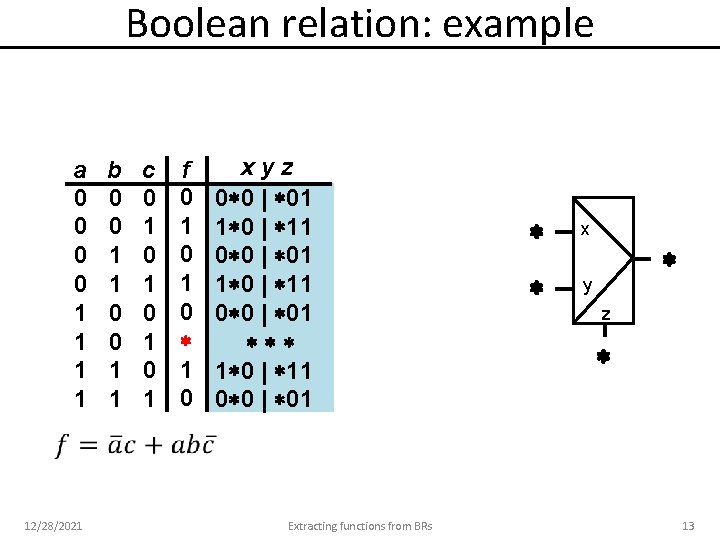
Boolean relation: example a 0 0 1 1 12/28/2021 b 0 0 1 1 c 0 1 0 1 f 0 1 0 xyz 0 0 | 01 1 0 | 11 0 0 | 01 Extracting functions from BRs x y z 13

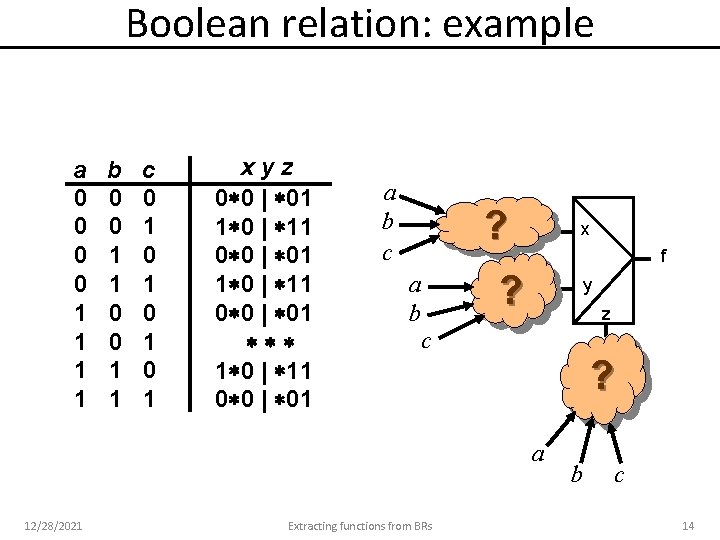
Boolean relation: example a 0 0 1 1 b 0 0 1 1 c 0 1 0 1 xyz 0 0 | 01 1 0 | 11 0 0 | 01 a b c ? a b c x f ? y z ? a 12/28/2021 Extracting functions from BRs b c 14

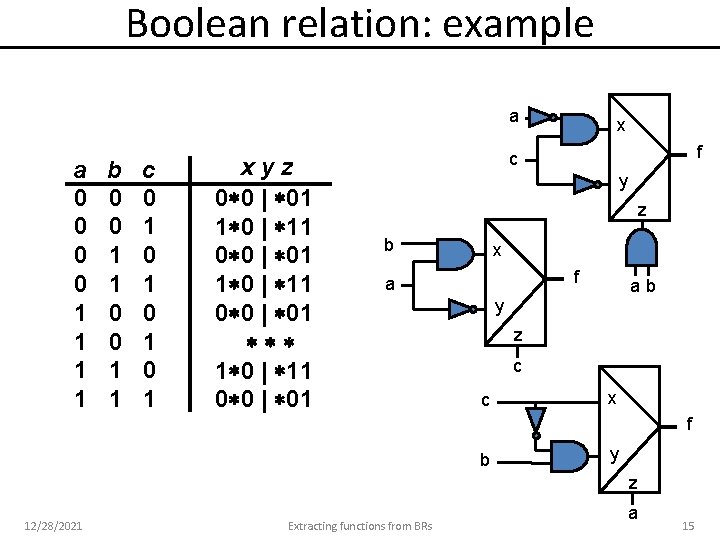
Boolean relation: example a a 0 0 1 1 b 0 0 1 1 c 0 1 0 1 xyz 0 0 | 01 1 0 | 11 0 0 | 01 x f c y z b x f a ab y z c c x f b y z 12/28/2021 Extracting functions from BRs a 15

BR: characteristic function 12/28/2021 Extracting functions from BRs 16

Solving a Boolean Relation 12/28/2021 Extracting functions from BRs 17

Solving a Boolean Relation 12/28/2021 Extracting functions from BRs 18

Exact 2 -level solvers The concept of prime must be redefined – F. Somenzi and R. K. Brayton (1989) • Method similar to Quine-Mc. Cluskey • Extension of primes to c-primes – S. Jeong and F. Somenzi (1992) • Formulate the problem as a Binate Covering Problem 12/28/2021 Extracting functions from BRs 19

Heuristic 2 -level solvers Based on ESPRESSO: – A. Ghosh, S. Devadas and A. R. Newton (1992) – Y. Watanabe and R. K. Brayton (1993) GYOCRO x: =Initial Solution; do REDUCE(x); EXPAND(x); IRREDUNDANT(x); while x is improved; 12/28/2021 Extracting functions from BRs 20

Modern approaches • Jie-Hong R. Jiang, Hsuan-Po Lin and Wei-Lun Hung, Interpolating Functions from Large Boolean Relations, ICCAD 2009. • David Bañeres, Jordi Cortadella, and Mike Kishinevsky, A Recursive Paradigm to Solve Boolean Relations, DAC 2004.

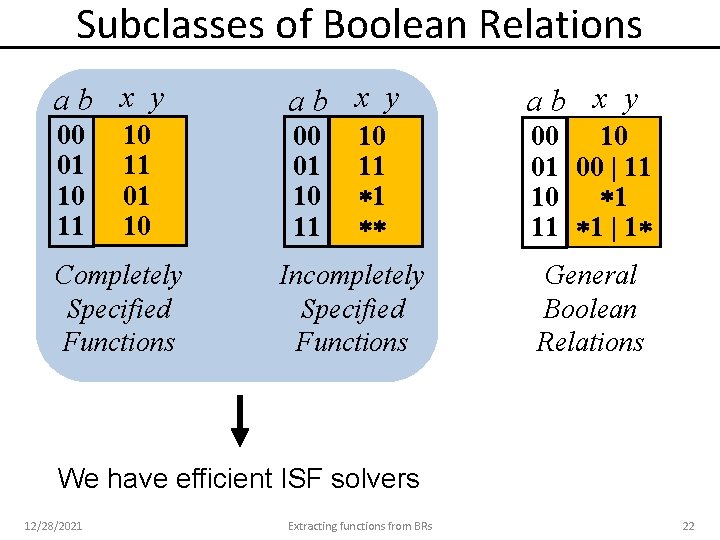
Subclasses of Boolean Relations ab x y 00 01 10 11 01 10 Completely Specified Functions ab x y 00 01 10 11 1 Incompletely Specified Functions ab x y 00 10 01 00 | 11 10 1 11 1 | 1 General Boolean Relations We have efficient ISF solvers 12/28/2021 Extracting functions from BRs 22

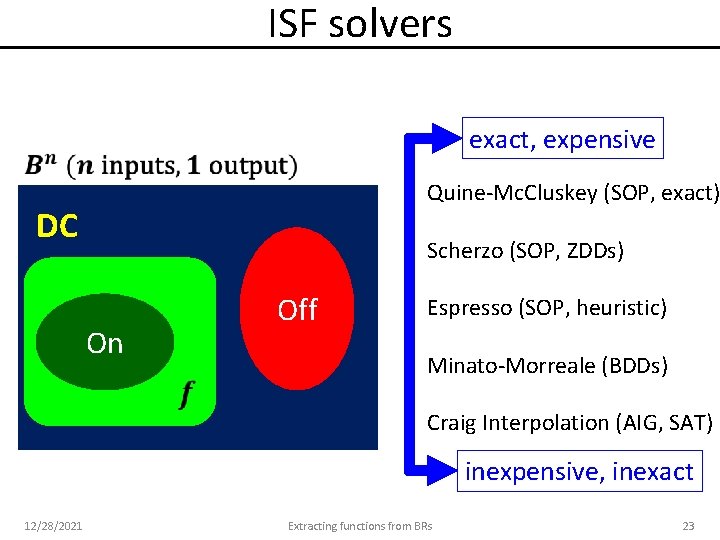
ISF solvers exact, expensive Quine-Mc. Cluskey (SOP, exact) DC Scherzo (SOP, ZDDs) On Off Espresso (SOP, heuristic) Minato-Morreale (BDDs) Craig Interpolation (AIG, SAT) inexpensive, inexact 12/28/2021 Extracting functions from BRs 23

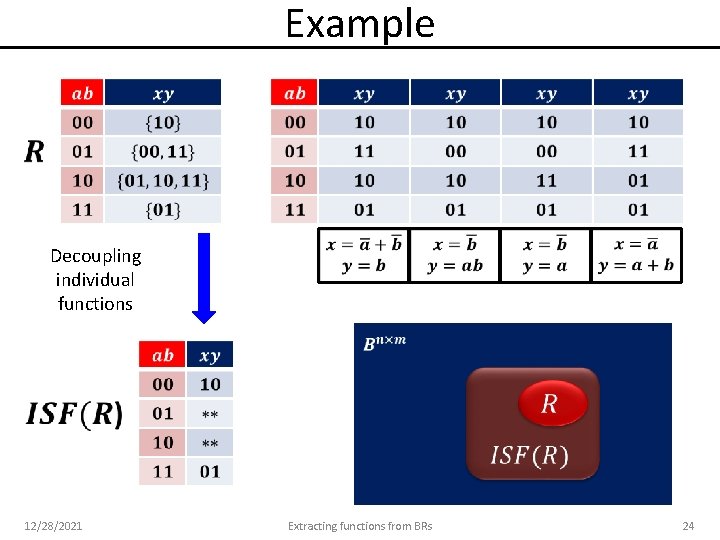
Example Decoupling individual functions 12/28/2021 Extracting functions from BRs 24

Decoupling the outputs Decoupling individual functions Easy implementation with BDDs or AIGs 12/28/2021 Extracting functions from BRs 25

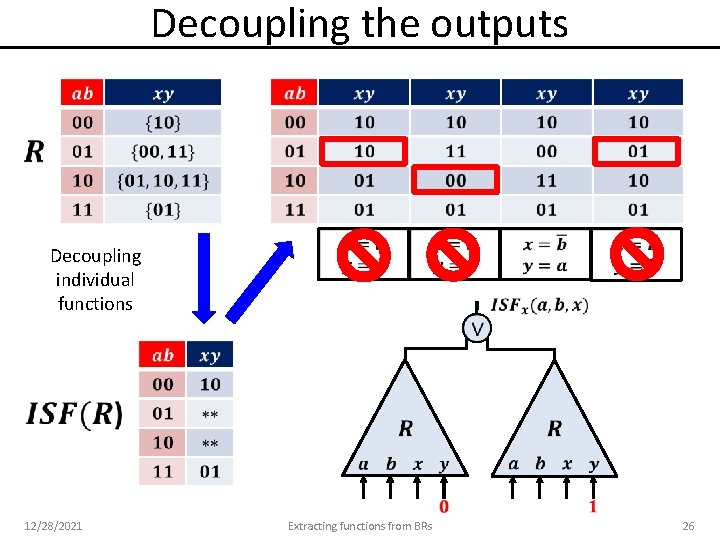
Decoupling the outputs Decoupling individual functions 12/28/2021 Extracting functions from BRs 26

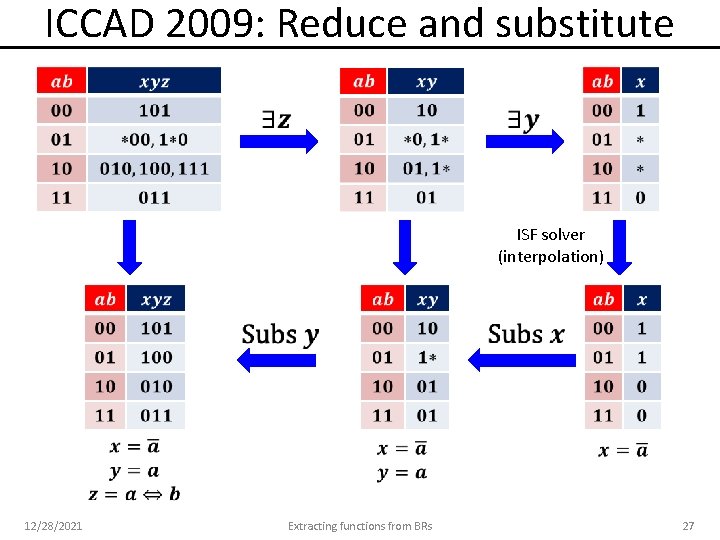
ICCAD 2009: Reduce and substitute ISF solver (interpolation) 12/28/2021 Extracting functions from BRs 27

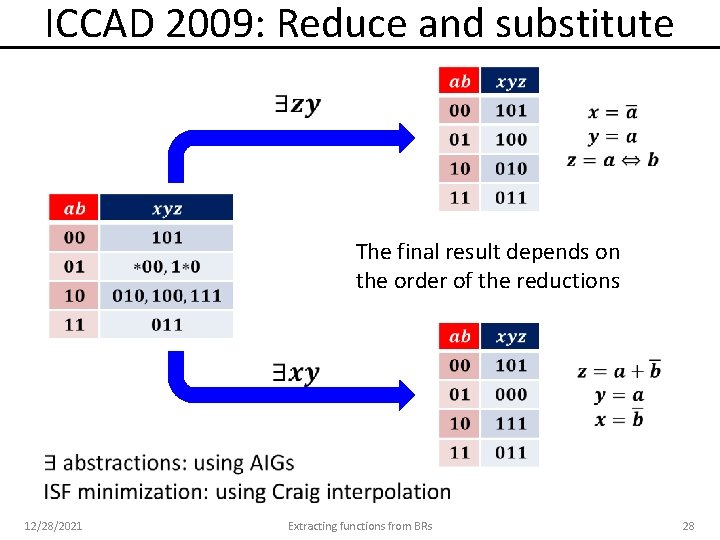
ICCAD 2009: Reduce and substitute The final result depends on the order of the reductions 12/28/2021 Extracting functions from BRs 28

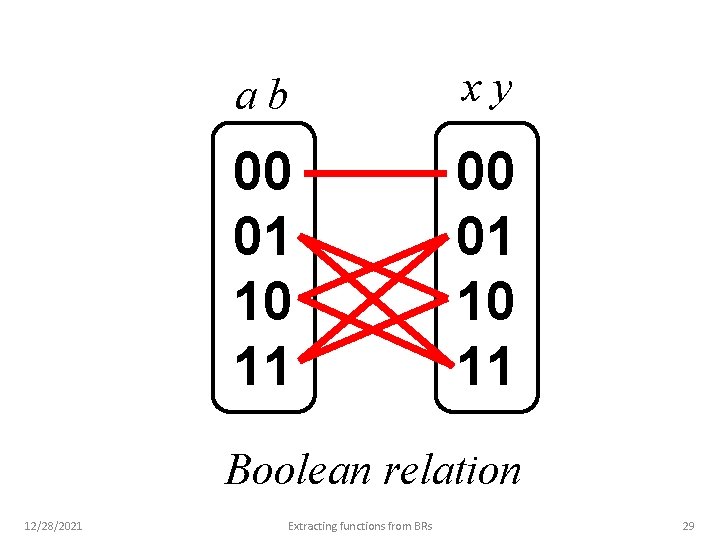
ab xy 00 01 10 11 Boolean relation 12/28/2021 Extracting functions from BRs 29

00 01 10 11 12/28/2021 00 01 10 11 Extracting functions from BRs

00 01 10 11 12/28/2021 00 01 10 11 Extracting functions from BRs

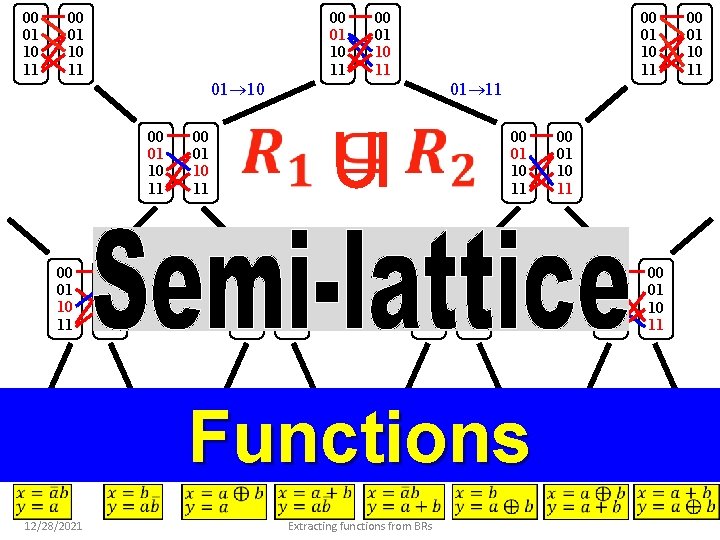
00 01 10 11 00 01 10 11 01 10 00 01 10 11 00 01 10 11 12/28/2021 00 01 10 11 01 11 00 01 10 11 00 01 10 11 00 01 10 11 Extracting functions from BRs 00 01 10 11 Functions 00 01 10 11 00 01 10 11 00 01 10 11

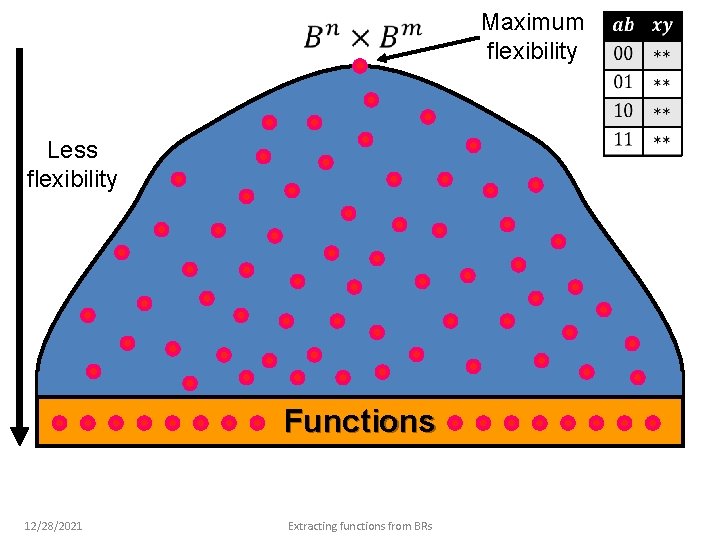
Maximum flexibility Less flexibility Functions 12/28/2021 Extracting functions from BRs

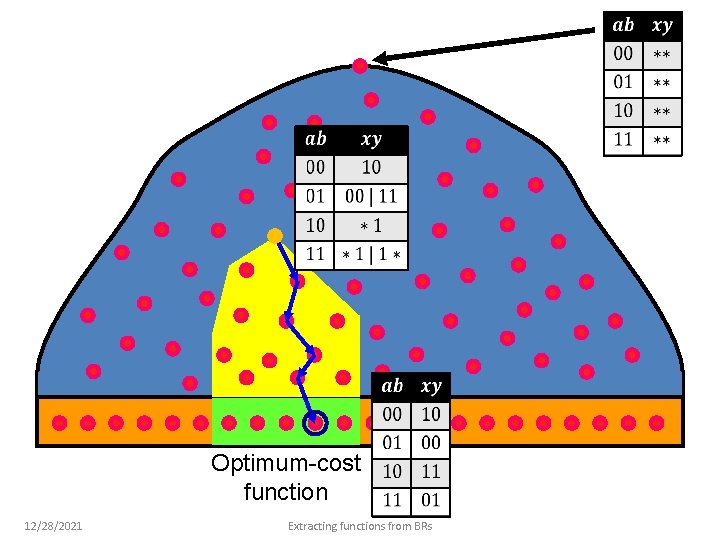
Optimum-cost function 12/28/2021 Extracting functions from BRs

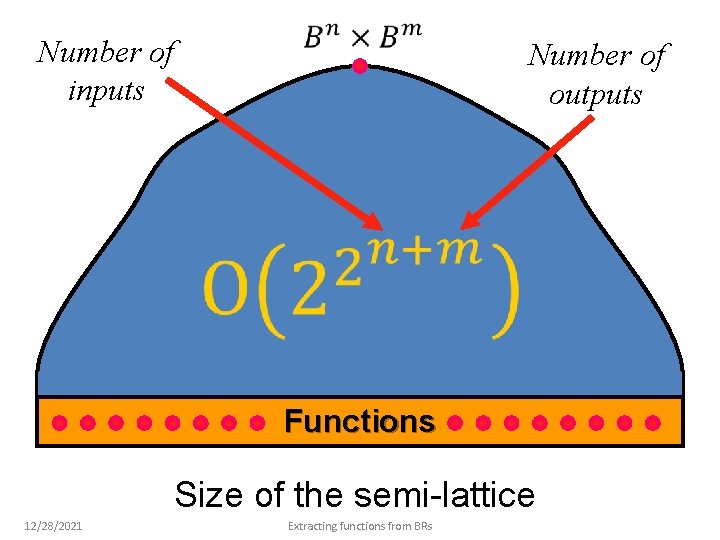
Number of inputs Number of outputs Functions Size of the semi-lattice 12/28/2021 Extracting functions from BRs

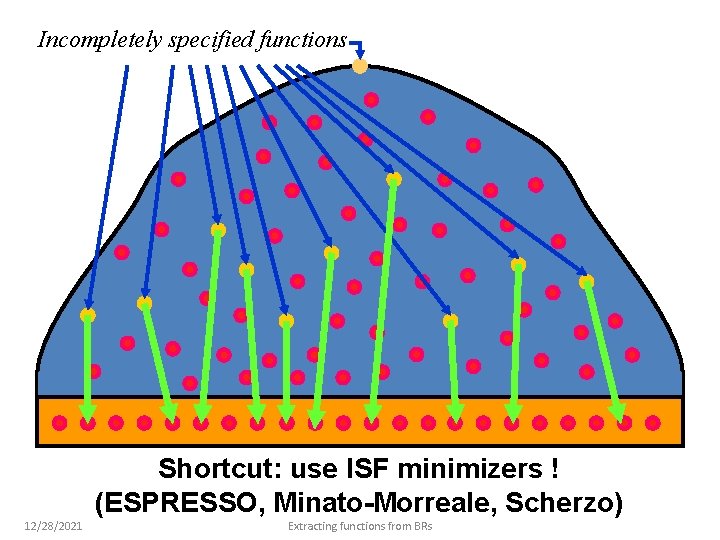
Incompletely specified functions Shortcut: use ISF minimizers ! (ESPRESSO, Minato-Morreale, Scherzo) 12/28/2021 Extracting functions from BRs

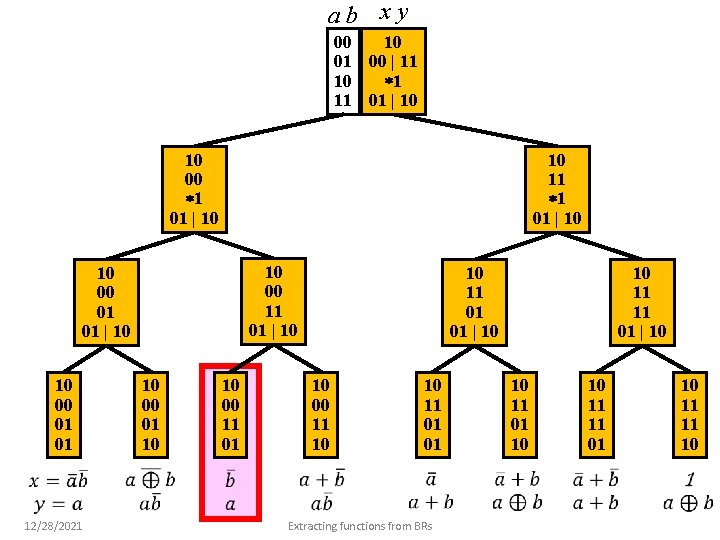
ab xy 10 00 01 00 | 11 1 10 11 01 | 10 10 00 1 01 | 10 10 11 1 01 | 10 10 00 11 01 | 10 10 00 01 01 12/28/2021 10 00 01 10 10 00 11 01 10 11 01 01 | 10 10 00 11 10 10 11 01 01 Extracting functions from BRs 10 11 11 01 | 10 10 11 01 10 10 11 11 01 10 11 11 10

The recursive approach (DAC 2004, BREL)

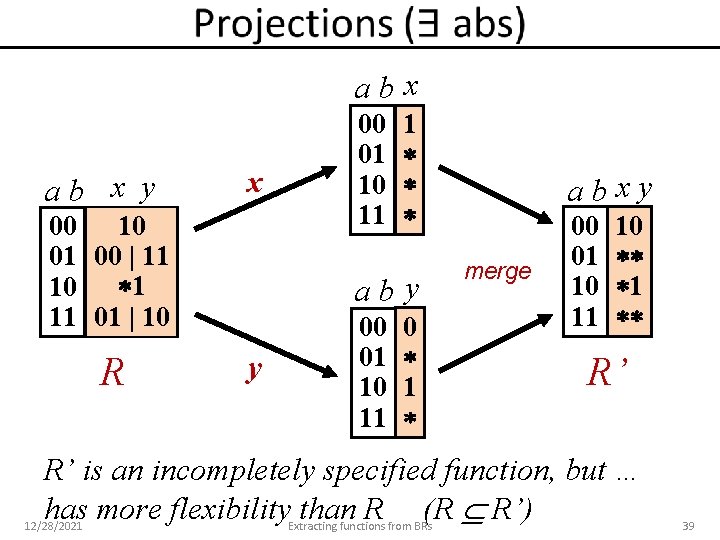
abx ab x y x 00 10 01 00 | 11 10 1 11 01 | 10 R 00 01 10 11 1 aby y 00 01 10 11 0 1 abxy merge 00 01 10 1 R’ R’ is an incompletely specified function, but … has more flexibility than R (R R’) 12/28/2021 Extracting functions from BRs 39

ISF BR projection 12/28/2021 Extracting functions from BRs 40

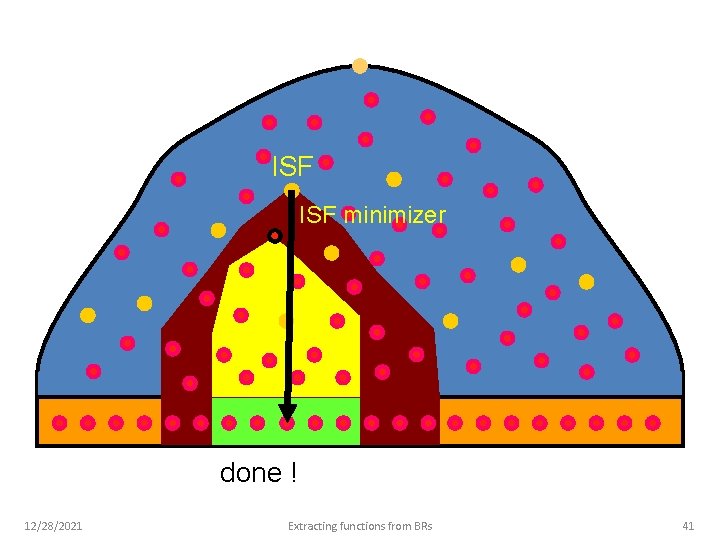
ISF minimizer done ! 12/28/2021 Extracting functions from BRs 41

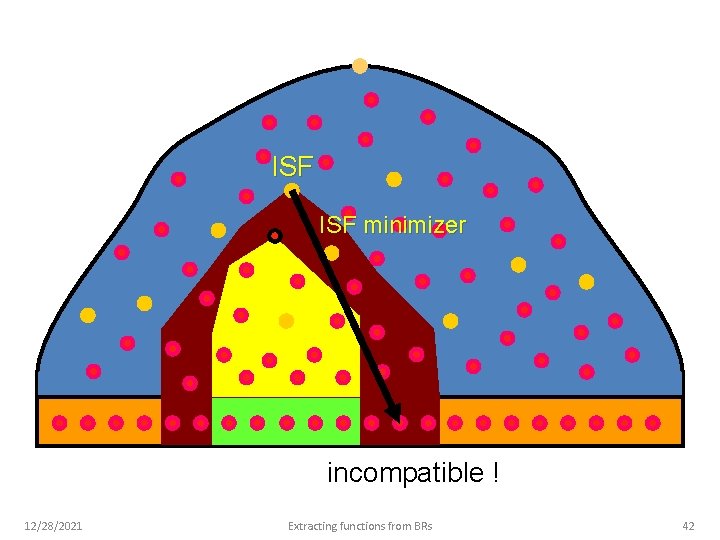
ISF minimizer incompatible ! 12/28/2021 Extracting functions from BRs 42

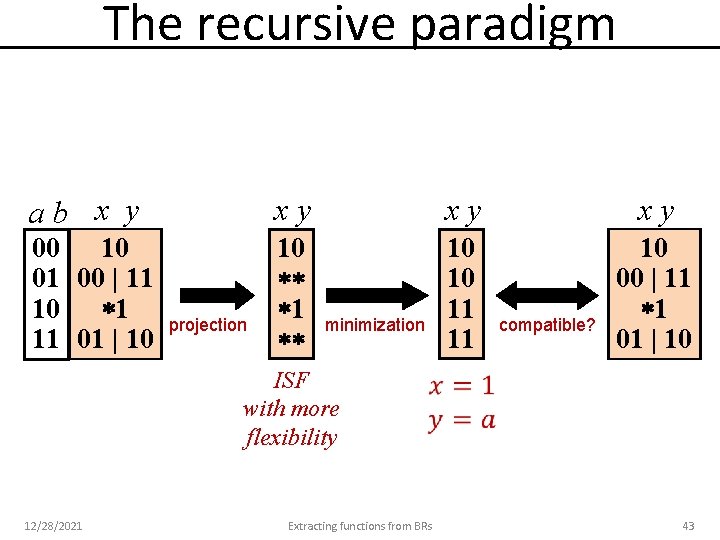
The recursive paradigm ab x y xy xy xy 00 10 01 00 | 11 10 1 11 01 | 10 10 11 11 10 00 | 11 1 01 | 10 projection minimization compatible? ISF with more flexibility 12/28/2021 Extracting functions from BRs 43

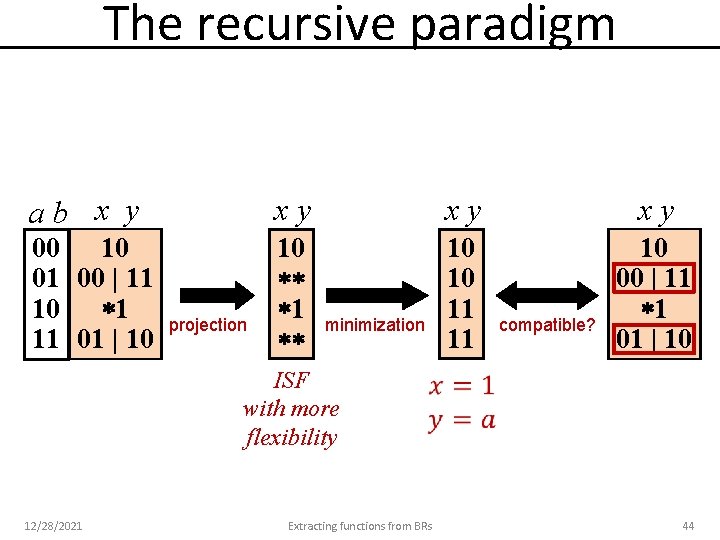
The recursive paradigm ab x y xy xy xy 00 10 01 00 | 11 10 1 11 01 | 10 10 11 11 10 00 | 11 1 01 | 10 projection minimization compatible? ISF with more flexibility 12/28/2021 Extracting functions from BRs 44

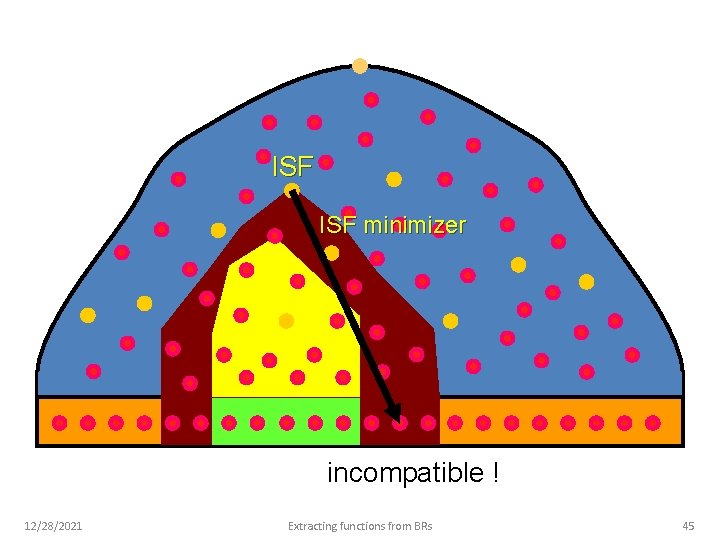
ISF minimizer incompatible ! 12/28/2021 Extracting functions from BRs 45

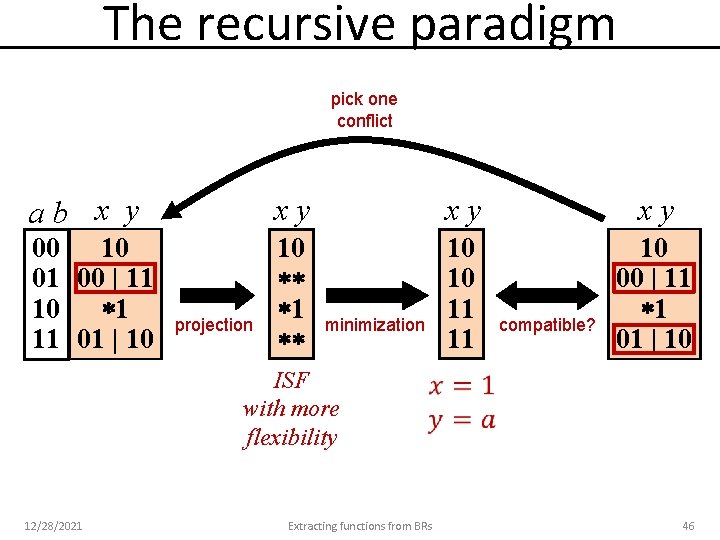
The recursive paradigm pick one conflict ab x y xy xy xy 00 10 01 00 | 11 10 1 11 01 | 10 10 11 11 10 00 | 11 1 01 | 10 projection minimization compatible? ISF with more flexibility 12/28/2021 Extracting functions from BRs 46

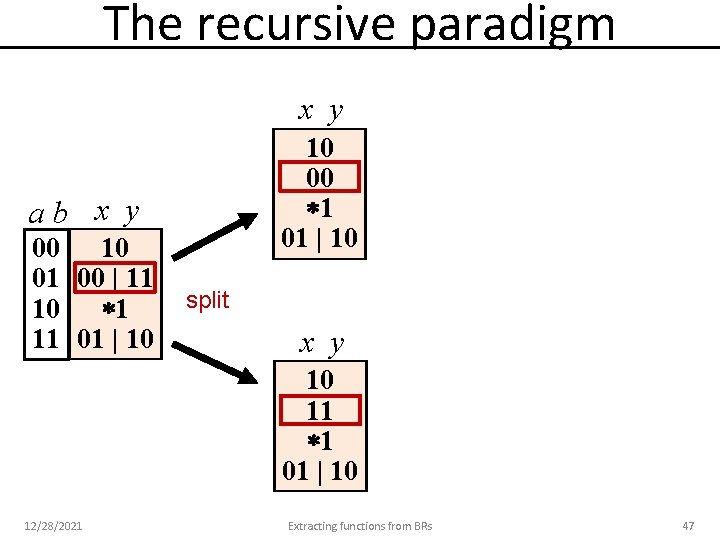
The recursive paradigm x y 10 00 1 01 | 10 ab x y 00 10 01 00 | 11 10 1 11 01 | 10 split x y 10 11 1 01 | 10 12/28/2021 Extracting functions from BRs 47

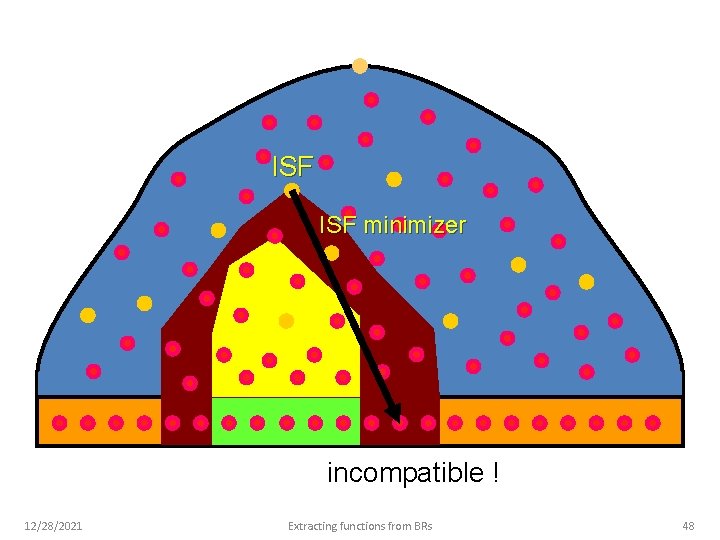
ISF minimizer incompatible ! 12/28/2021 Extracting functions from BRs 48

BR 1 BR 2 12/28/2021 Extracting functions from BRs 49

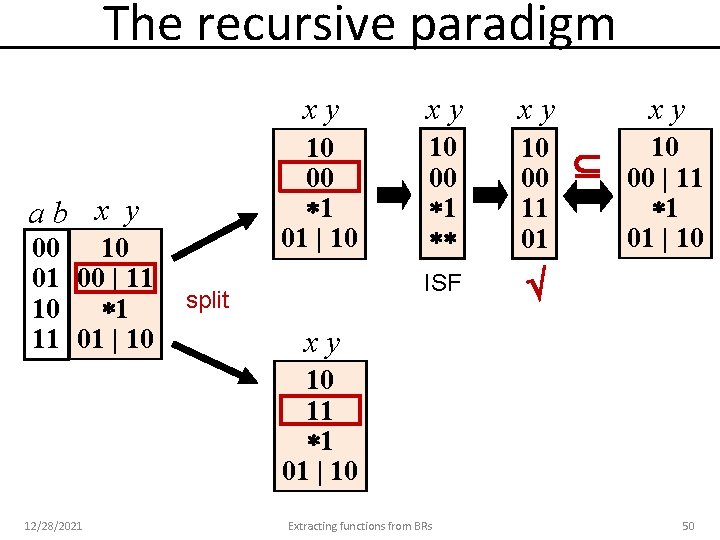
The recursive paradigm ab x y 00 10 01 00 | 11 10 1 11 01 | 10 xy xy xy 10 00 1 01 | 10 10 00 11 01 ISF split xy 10 00 | 11 1 01 | 10 xy 10 11 1 01 | 10 12/28/2021 Extracting functions from BRs 50

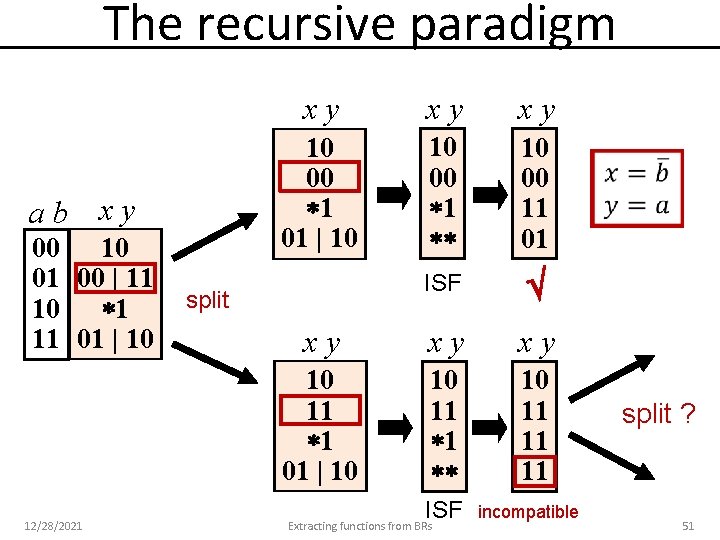
The recursive paradigm ab xy 00 10 01 00 | 11 10 1 11 01 | 10 12/28/2021 xy xy xy 10 00 1 01 | 10 10 00 11 01 ISF xy xy xy 10 11 1 01 | 10 10 11 11 11 split ISF Extracting functions from BRs incompatible split ? 51

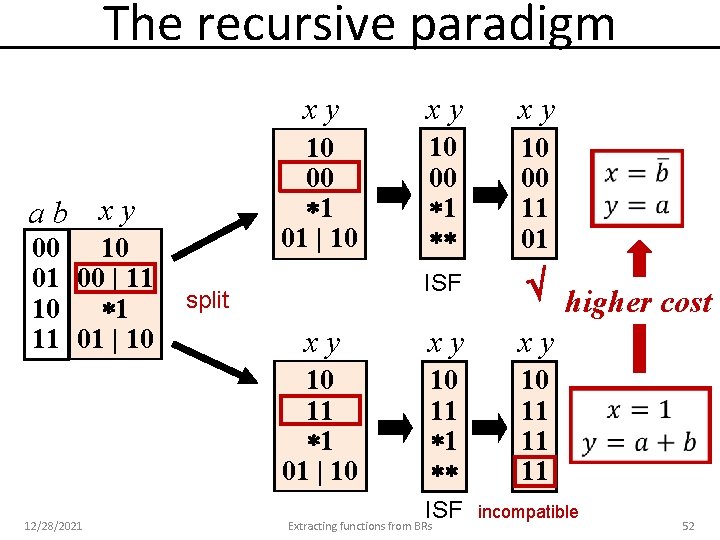
The recursive paradigm ab xy 00 10 01 00 | 11 10 1 11 01 | 10 12/28/2021 xy xy xy 10 00 1 01 | 10 10 00 11 01 ISF higher cost split xy xy xy 10 11 1 01 | 10 10 11 11 11 ISF Extracting functions from BRs incompatible 52

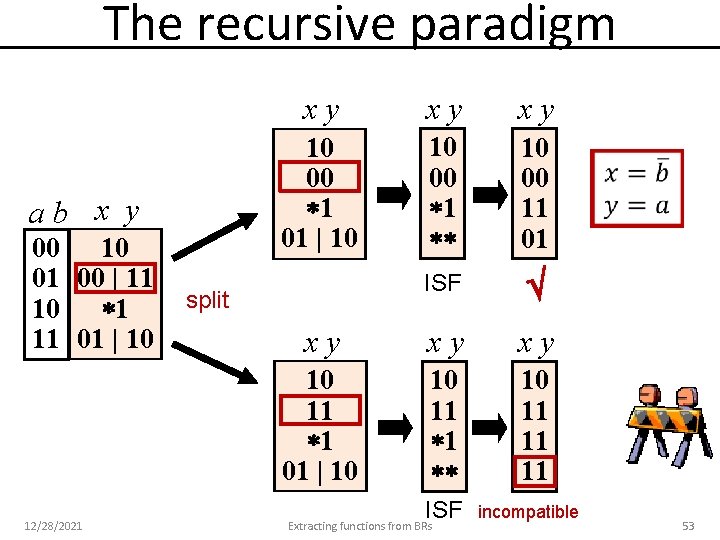
The recursive paradigm ab x y 00 10 01 00 | 11 10 1 11 01 | 10 12/28/2021 xy xy xy 10 00 1 01 | 10 10 00 11 01 ISF xy xy xy 10 11 1 01 | 10 10 11 11 11 split ISF Extracting functions from BRs incompatible 53

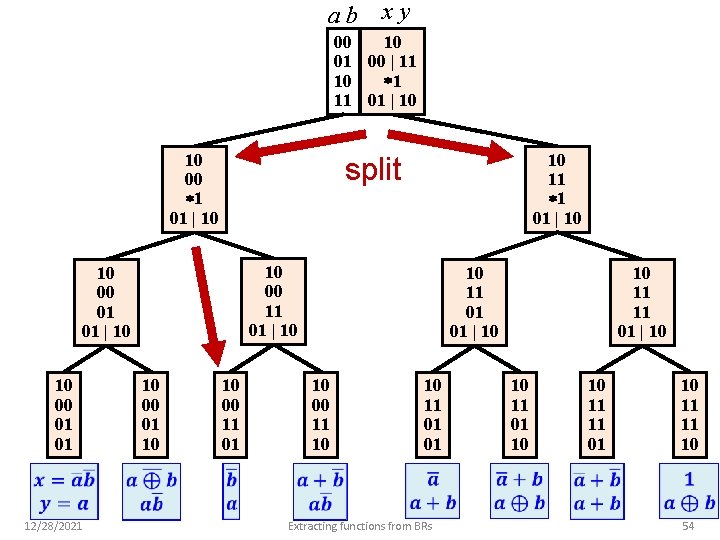
ab xy 10 00 01 00 | 11 1 10 11 01 | 10 10 00 01 01 12/28/2021 10 11 1 01 | 10 split 10 00 01 10 10 00 11 01 10 11 01 01 | 10 10 00 11 10 10 11 01 01 Extracting functions from BRs 10 11 11 01 | 10 10 11 01 10 10 11 11 01 10 11 11 10 54

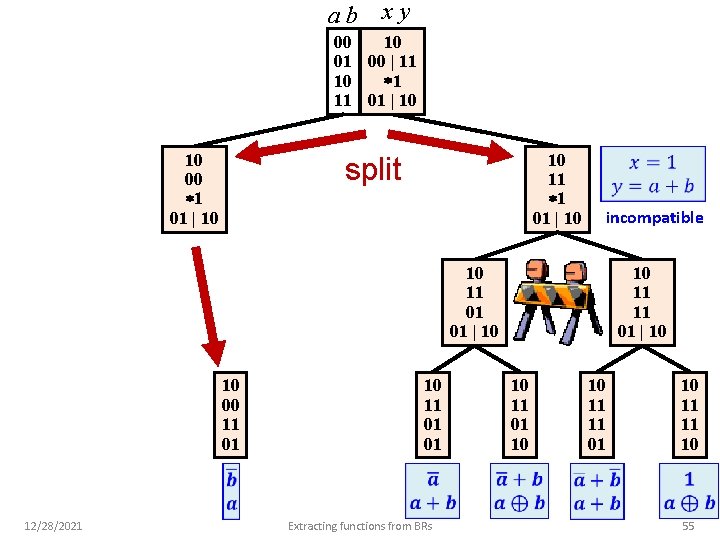
ab xy 10 00 01 00 | 11 1 10 11 01 | 10 10 00 1 01 | 10 10 11 1 01 | 10 split incompatible 10 11 01 01 | 10 10 00 11 01 12/28/2021 10 11 01 01 Extracting functions from BRs 10 11 11 01 | 10 10 11 01 10 10 11 11 01 10 11 11 10 55

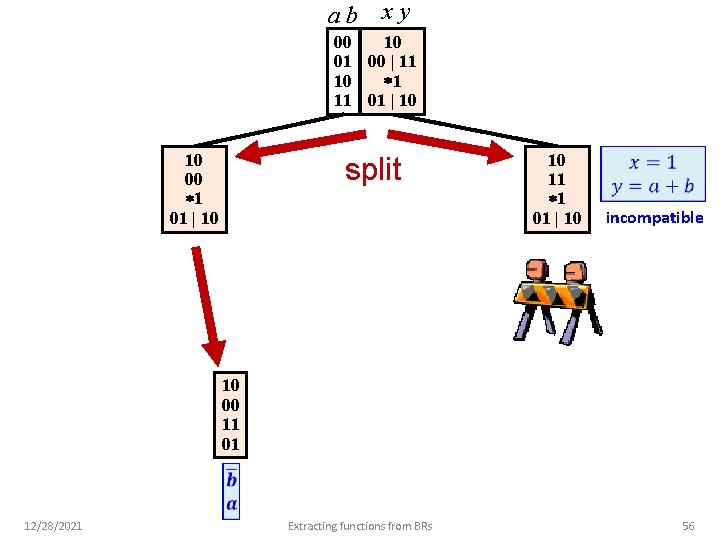
ab xy 10 00 01 00 | 11 1 10 11 01 | 10 10 00 1 01 | 10 split 10 11 1 01 | 10 incompatible 10 00 11 01 12/28/2021 Extracting functions from BRs 56

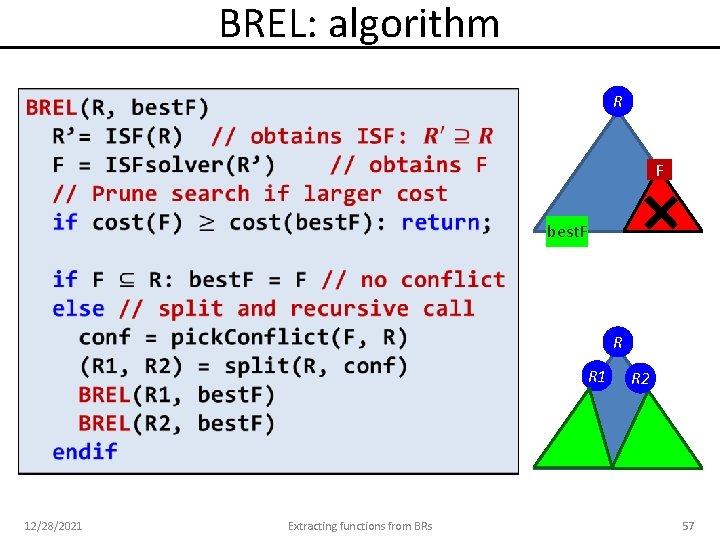
BREL: algorithm R F best. F R R 1 12/28/2021 Extracting functions from BRs R 2 57

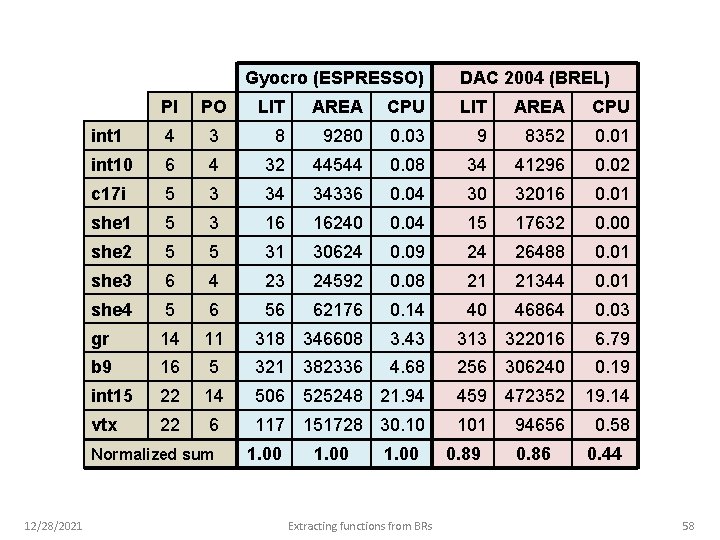
Gyocro (ESPRESSO) 12/28/2021 PI PO int 1 4 int 10 DAC 2004 (BREL) LIT AREA CPU 3 8 9280 0. 03 9 8352 0. 01 6 4 32 44544 0. 08 34 41296 0. 02 c 17 i 5 3 34 34336 0. 04 30 32016 0. 01 she 1 5 3 16 16240 0. 04 15 17632 0. 00 she 2 5 5 31 30624 0. 09 24 26488 0. 01 she 3 6 4 23 24592 0. 08 21 21344 0. 01 she 4 5 6 56 62176 0. 14 40 46864 0. 03 gr 14 11 318 346608 3. 43 313 322016 6. 79 b 9 16 5 321 382336 4. 68 256 306240 0. 19 int 15 22 14 506 525248 21. 94 459 472352 19. 14 vtx 22 6 117 151728 30. 10 101 94656 0. 58 Normalized sum 1. 00 Extracting functions from BRs 0. 89 0. 86 0. 44 58

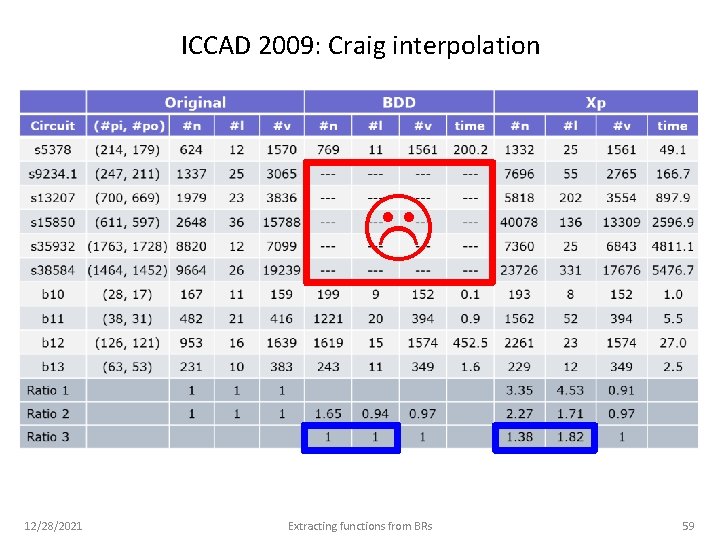
ICCAD 2009: Craig interpolation 12/28/2021 Extracting functions from BRs 59

Conclusions • Two options to solve Boolean Relations (applicable to other CS problems): – Exploit the knowledge we have about our problem and use smart algorithms. – “Admit” the lack of knowledge about of our problem and … (guess what) use Machine Learning. • Our knowledge: – We know about SAT, AIGs, BDDs, ISF, Craig interpolants, … – The semi-lattice of Boolean Relations is infested by ISFs! • Two ways: – Small and accurate (BDDs, recursive, Branch & Bound). – Large and less accurate (AIGs, SAT, Craig interpolants). • Can both methods be combined? 12/28/2021 Extracting functions from BRs 60