Extra Dimensions From Colliders to Cosmology Large Extra

Extra Dimensions: From Colliders to Cosmology • Large Extra Dimensions (Primordial Black Holes) • Universal Extra Dimensions (KK Bino) • Warped Extra Dimensions (KK R ) Collider signals & DM properties* * Thanks to T. Tait! J. Hewett Michell Symposium 2007

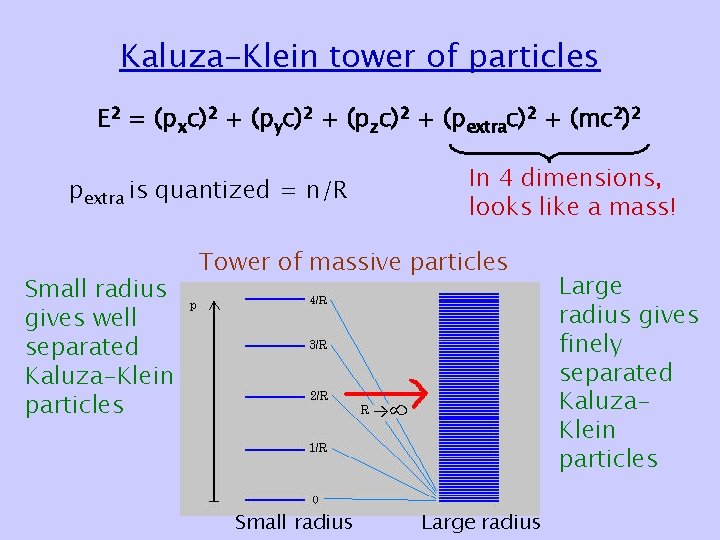
Kaluza-Klein tower of particles E 2 = (pxc)2 + (pyc)2 + (pzc)2 + (pextrac)2 + (mc 2)2 pextra is quantized = n/R Small radius gives well separated Kaluza-Klein particles In 4 dimensions, looks like a mass! Tower of massive particles Small radius Large radius gives finely separated Kaluza. Klein particles

Large Extra Dimensions Arkani-Hamed, Dimopoulos, Dvali, SLAC-PUB-7801 Motivation: solve the hierarchy problem by removing it! SM fields confined to 3 -brane Gravity becomes strong in the bulk Gauss’ Law: MPl 2 = V MD 2+ , V = Rc MD = Fundamental scale in the bulk ~ Te. V

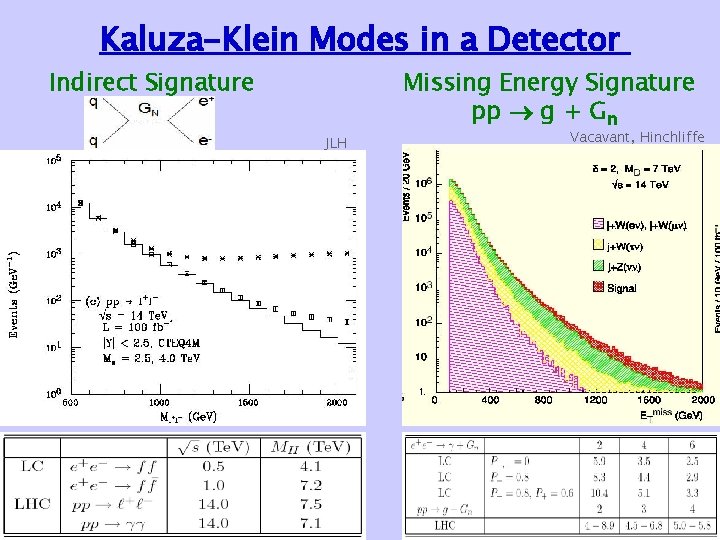
Kaluza-Klein Modes in a Detector Indirect Signature Missing Energy Signature pp g + Gn JLH Vacavant, Hinchliffe

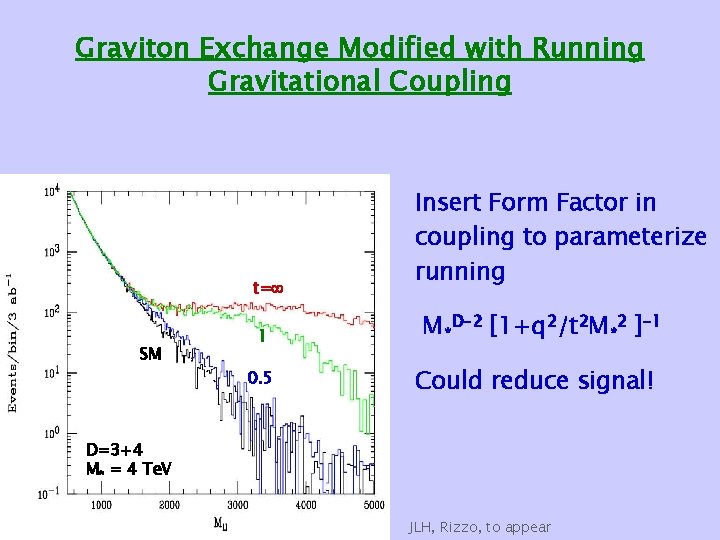
Graviton Exchange Modified with Running Gravitational Coupling t= SM 1 0. 5 Insert Form Factor in coupling to parameterize running M*D-2 [1+q 2/t 2 M*2 ]-1 Could reduce signal! D=3+4 M* = 4 Te. V JLH, Rizzo, to appear

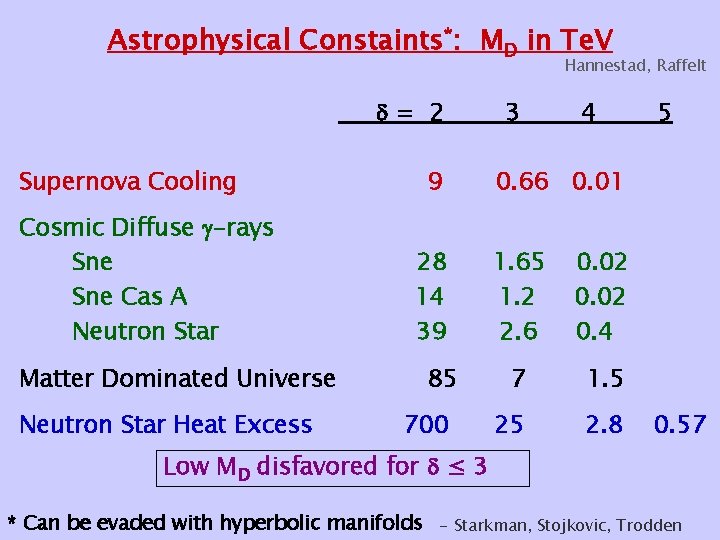
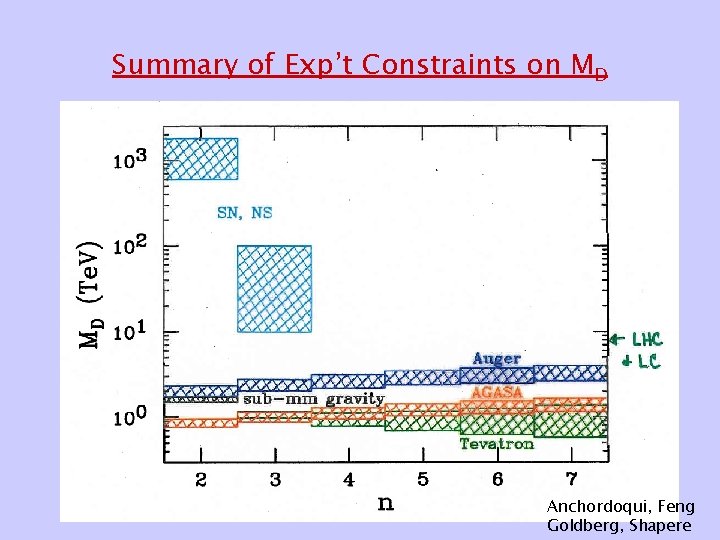
Constraints from Astrophysics/Cosmology • Supernova Cooling Cullen, Perelstein Barger etal, Savage etal NN + Gn can cool supernova too rapidly • Cosmic Diffuse Rays NN + Gn - G n Hannestad, Raffelt Hall, Smith • Matter Dominated Universe Fairbairn • Neutron Star Heat Excess Hannestad, Raffelt too many KK states NN + Gn becomes trapped in neutron star halo and heats it

Astrophysical Constaints*: MD in Te. V Hannestad, Raffelt = 2 Supernova Cooling Cosmic Diffuse -rays Sne Cas A Neutron Star 9 28 14 39 Matter Dominated Universe Neutron Star Heat Excess 85 700 3 4 5 0. 66 0. 01 1. 65 1. 2 2. 6 0. 02 0. 4 7 1. 5 25 2. 8 0. 57 Low MD disfavored for ≤ 3 * Can be evaded with hyperbolic manifolds - Starkman, Stojkovic, Trodden

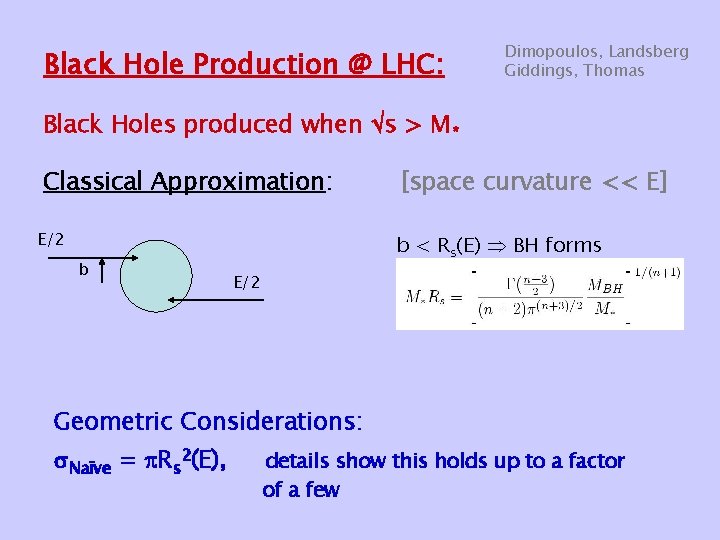
Black Hole Production @ LHC: Dimopoulos, Landsberg Giddings, Thomas Black Holes produced when s > M* Classical Approximation: E/2 b [space curvature << E] b < Rs(E) BH forms E/2 Geometric Considerations: Naïve = Rs 2(E), details show this holds up to a factor of a few

Black Hole event simulation @ LHC

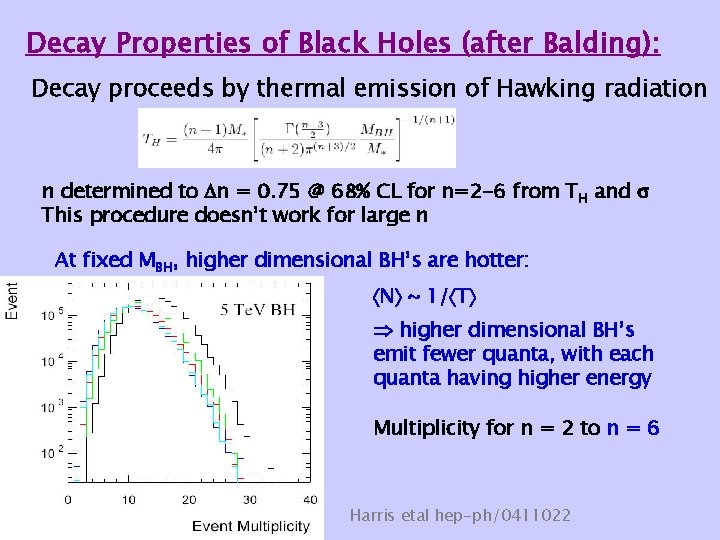
Decay Properties of Black Holes (after Balding): Decay proceeds by thermal emission of Hawking radiation n determined to n = 0. 75 @ 68% CL for n=2 -6 from TH and This procedure doesn’t work for large n At fixed MBH, higher dimensional BH’s are hotter: N ~ 1/ T higher dimensional BH’s emit fewer quanta, with each quanta having higher energy Multiplicity for n = 2 to n = 6 Harris etal hep-ph/0411022

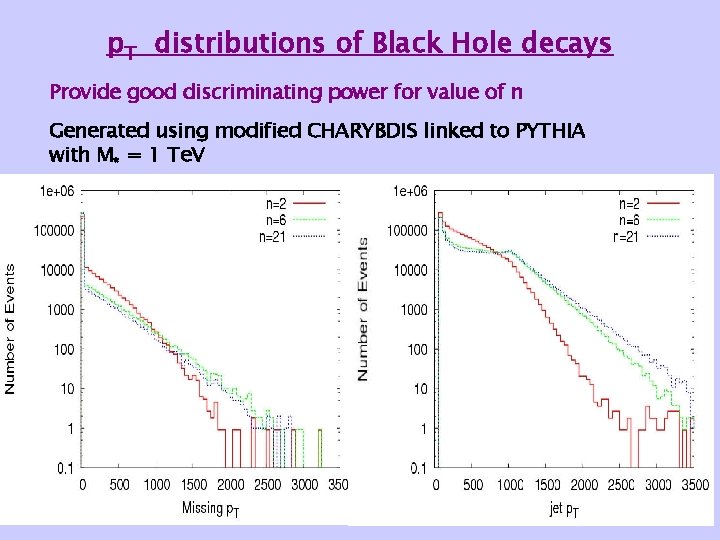
p. T distributions of Black Hole decays Provide good discriminating power for value of n Generated using modified CHARYBDIS linked to PYTHIA with M* = 1 Te. V

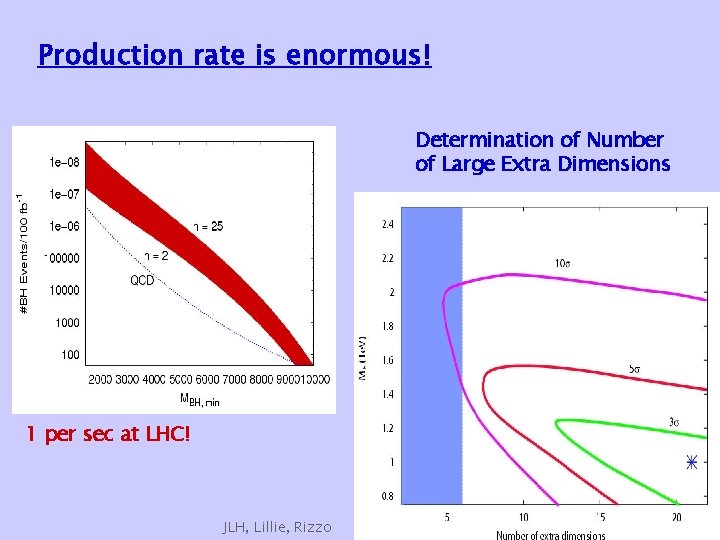
Production rate is enormous! Determination of Number of Large Extra Dimensions 1 per sec at LHC! JLH, Lillie, Rizzo

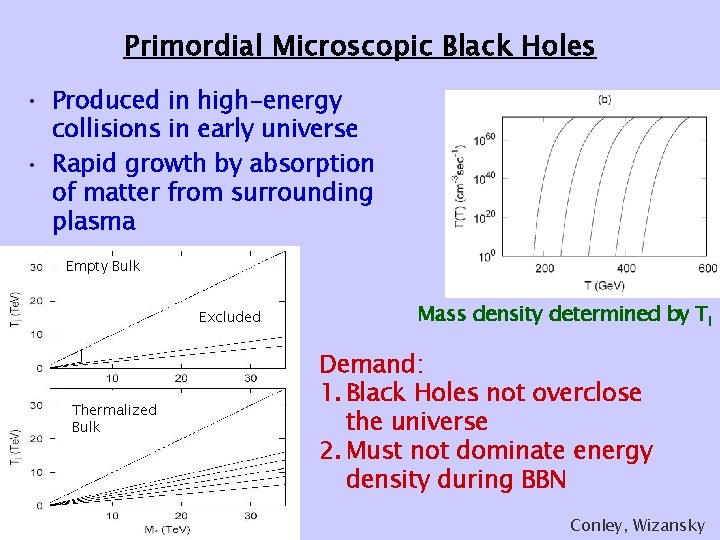
Primordial Microscopic Black Holes • Produced in high-energy collisions in early universe • Rapid growth by absorption of matter from surrounding plasma Empty Bulk Excluded Thermalized Bulk Mass density determined by TI Demand: 1. Black Holes not overclose the universe 2. Must not dominate energy density during BBN Conley, Wizansky

Universal Extra Dimensions Appelquist, Cheng, Dobrescu • All SM fields in Te. V-1, 5 d, S 1/Z 2 bulk • No branes! translational invariance is preserved tree-level conservation of p 5 • KK number conserved at tree-level broken at higher order by boundary terms • KK parity conserved to all orders, (-1)n Consequences: 1. KK excitations only produced in pairs Relaxation of collider & precision EW constraints Rc-1 ≥ 300 Ge. V! 2. Lightest KK particle is stable (LKP) and is Dark Matter candidate 3. Boundary terms separate masses and give SUSY-like spectrum

Universal Extra Dimensions: Bosonic SUSY Phenomenology looks like Supersymmetry: Spectrum looks like SUSY ! Heavier KK particles cascade down to LKP: Photon KK state appears as missing ET SUSY-like Spectroscopy Confusion with SUSY if discovered @ LHC ! Chang, Matchev, Schmaltz

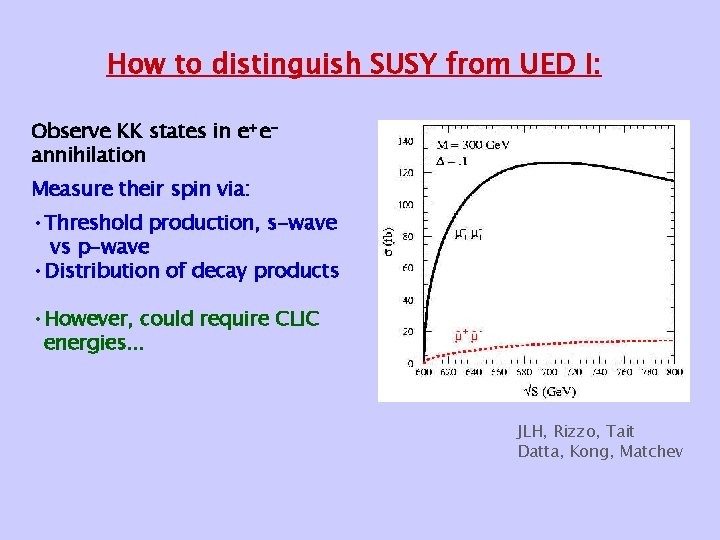
How to distinguish SUSY from UED I: Observe KK states in e+eannihilation Measure their spin via: • Threshold production, s-wave vs p-wave • Distribution of decay products • However, could require CLIC energies. . . JLH, Rizzo, Tait Datta, Kong, Matchev

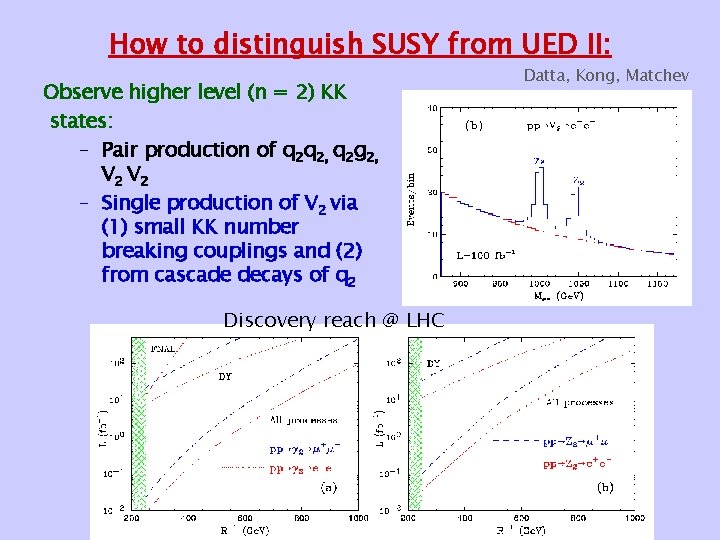
How to distinguish SUSY from UED II: Observe higher level (n = 2) KK states: – Pair production of q 2 q 2, q 2 g 2, V 2 – Single production of V 2 via (1) small KK number breaking couplings and (2) from cascade decays of q 2 Discovery reach @ LHC Datta, Kong, Matchev

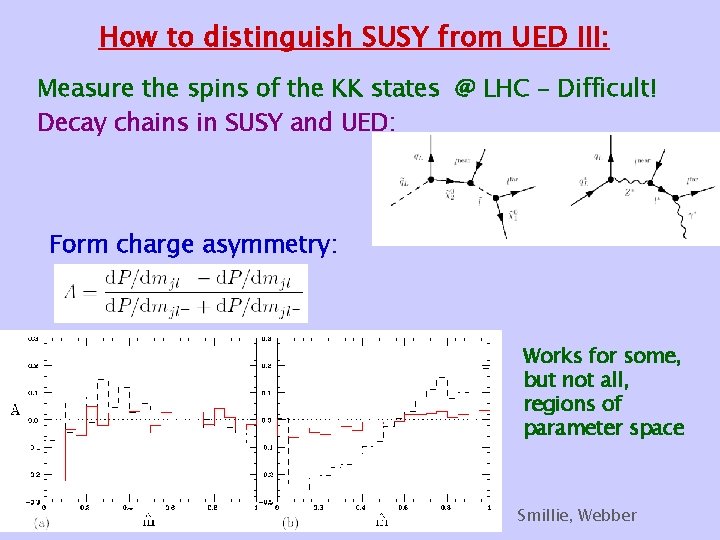
How to distinguish SUSY from UED III: Measure the spins of the KK states @ LHC – Difficult! Decay chains in SUSY and UED: Form charge asymmetry: Works for some, but not all, regions of parameter space Smillie, Webber

Identity of the LKP • Boundary terms (similar to SUSY soft-masses) – Induced @ loop-level (vanish @ cut-off) – Determine masses & couplings of entire KK tower • 1 ≪ 2 ≪ 3 – Smallest corrections to U(1) KK state – NLKP is e. R(1) • M ~ 1/R > v – LKP is almost pure Bino KK B (1) Bino-Wino mass matrix, n=1

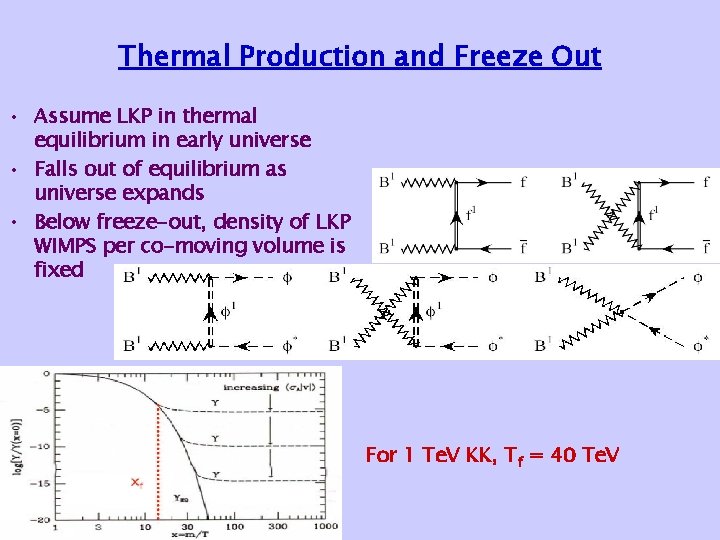
Thermal Production and Freeze Out • Assume LKP in thermal equilibrium in early universe • Falls out of equilibrium as universe expands • Below freeze-out, density of LKP WIMPS per co-moving volume is fixed For 1 Te. V KK, Tf = 40 Te. V

Co-annihilation • e. R(1) may substantially affect relic density if it is close in mass to B(1) • e. R(1) has same interaction efficiency – freeze-out temp is unaffected • e. R(1) left after freeze-out – Eventually e. R(1) e(0) + B(1) • Net relic density of B(1) is increased

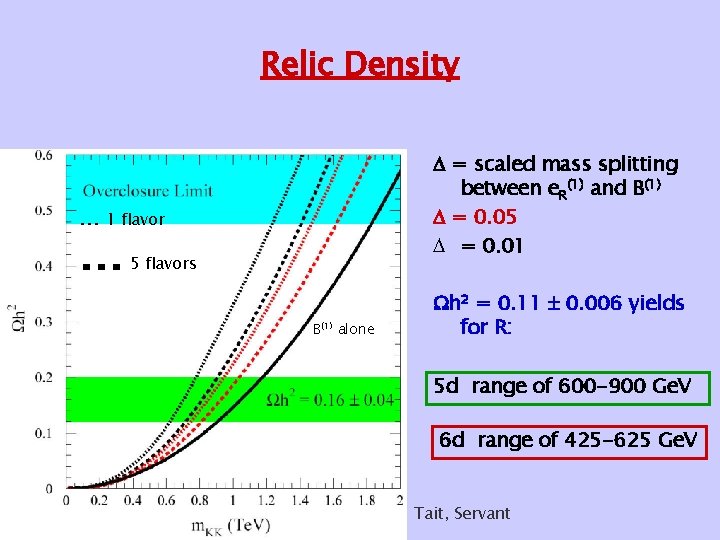
Relic Density … = scaled mass splitting between e. R(1) and B(1) = 0. 05 = 0. 01 1 flavor … 5 flavors B(1) alone h 2 = 0. 11 0. 006 yields for R: 5 d range of 600 -900 Ge. V 6 d range of 425 -625 Ge. V Tait, Servant

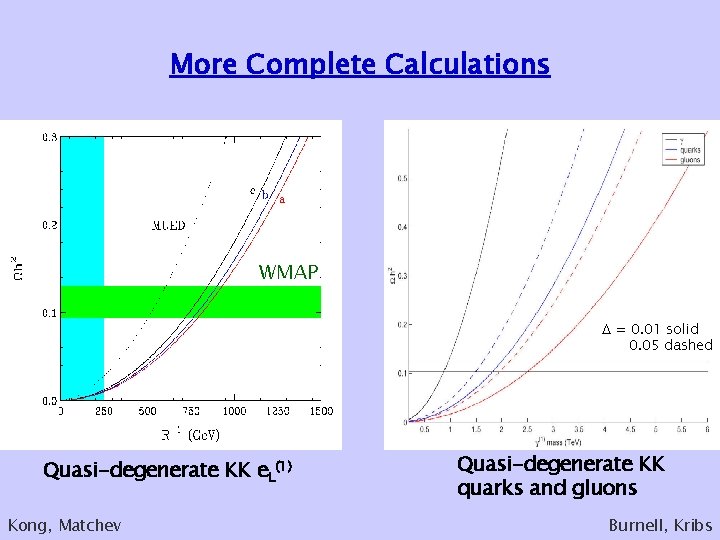
More Complete Calculations WMAP = 0. 01 solid 0. 05 dashed Quasi-degenerate KK e. L(1) Kong, Matchev Quasi-degenerate KK quarks and gluons Burnell, Kribs

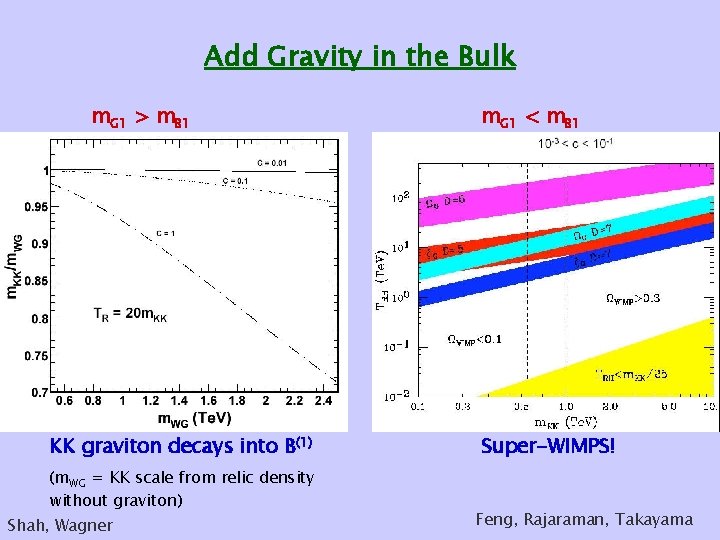
Add Gravity in the Bulk m. G 1 > m. B 1 KK graviton decays into B(1) (m. WG = KK scale from relic density without graviton) Shah, Wagner m. G 1 < m. B 1 Super-WIMPS! Feng, Rajaraman, Takayama

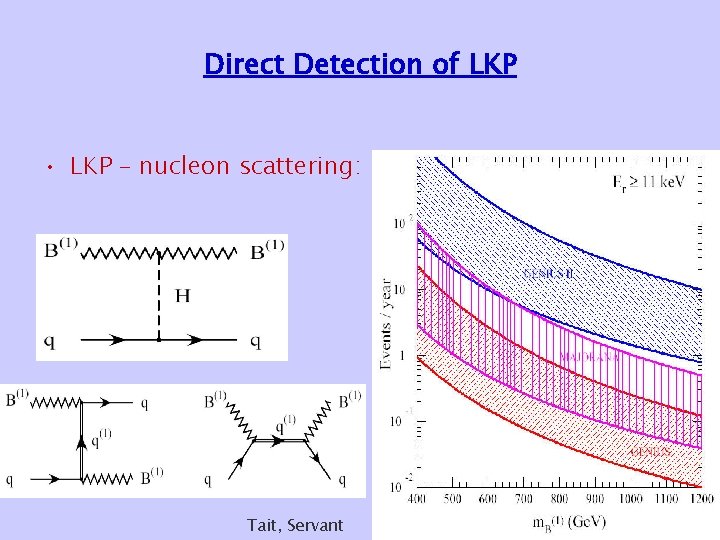
Direct Detection of LKP • LKP – nucleon scattering: Tait, Servant

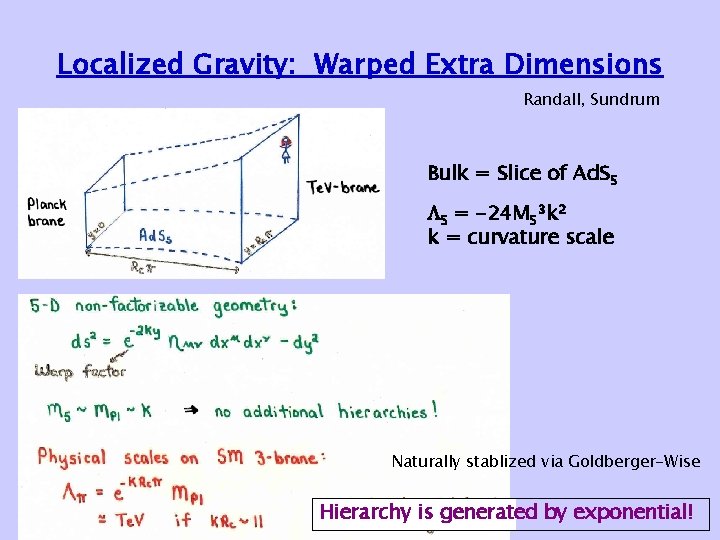
Localized Gravity: Warped Extra Dimensions Randall, Sundrum Bulk = Slice of Ad. S 5 5 = -24 M 53 k 2 k = curvature scale Naturally stablized via Goldberger-Wise Hierarchy is generated by exponential!

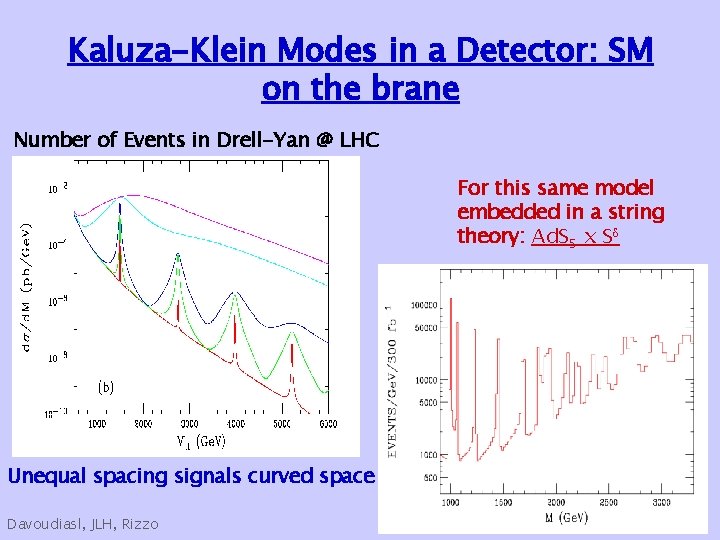
Kaluza-Klein Modes in a Detector: SM on the brane Number of Events in Drell-Yan @ LHC For this same model embedded in a string theory: Ad. S 5 x S Unequal spacing signals curved space Davoudiasl, JLH, Rizzo

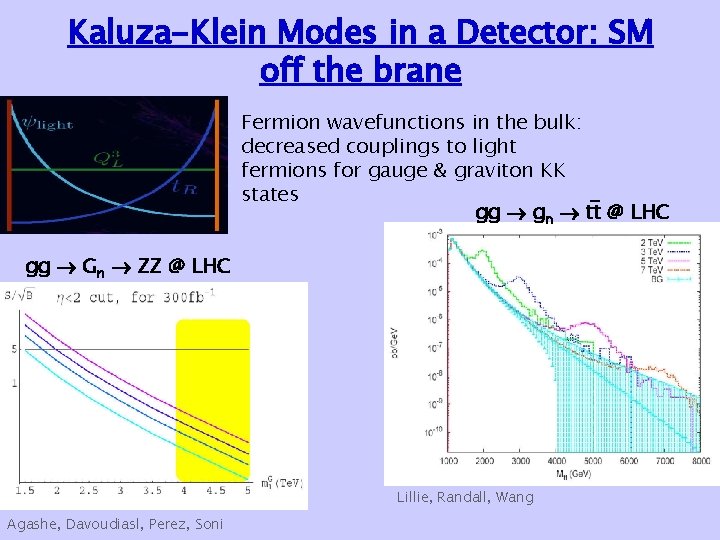
Kaluza-Klein Modes in a Detector: SM off the brane Fermion wavefunctions in the bulk: decreased couplings to light fermions for gauge & graviton KK states gg gn tt @ LHC gg Gn ZZ @ LHC Lillie, Randall, Wang Agashe, Davoudiasl, Perez, Soni

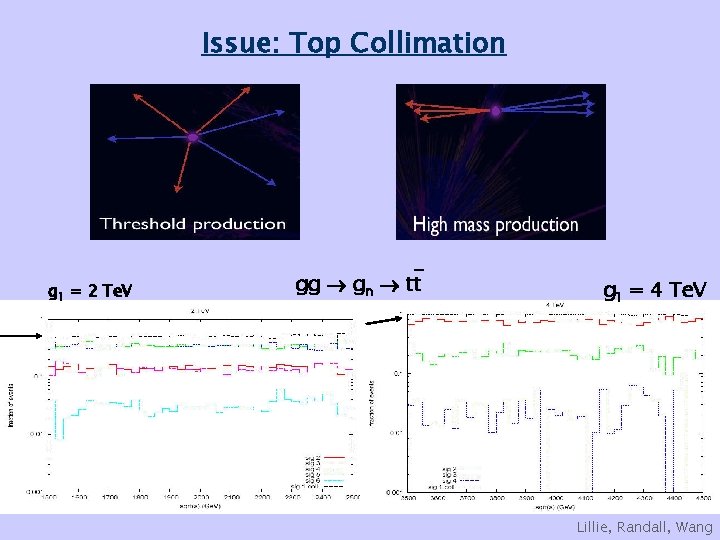
Issue: Top Collimation g 1 = 2 Te. V gg gn tt g 1 = 4 Te. V Lillie, Randall, Wang

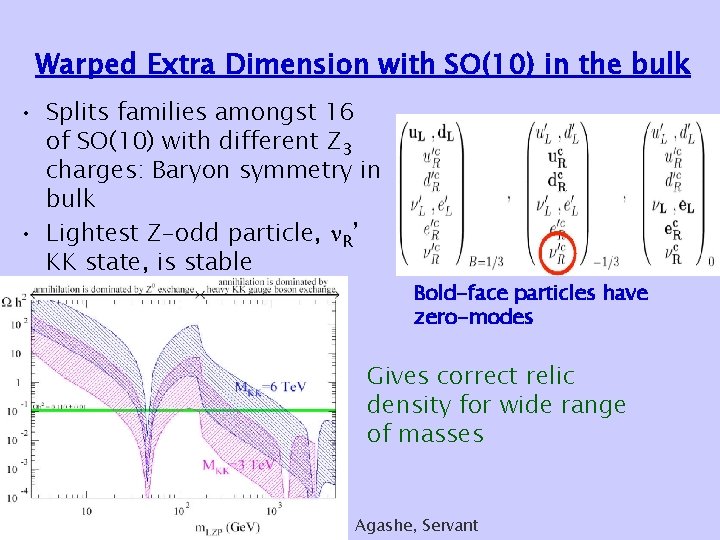
Warped Extra Dimension with SO(10) in the bulk • Splits families amongst 16 of SO(10) with different Z 3 charges: Baryon symmetry in bulk • Lightest Z-odd particle, R’ KK state, is stable Bold-face particles have zero-modes Gives correct relic density for wide range of masses Agashe, Servant

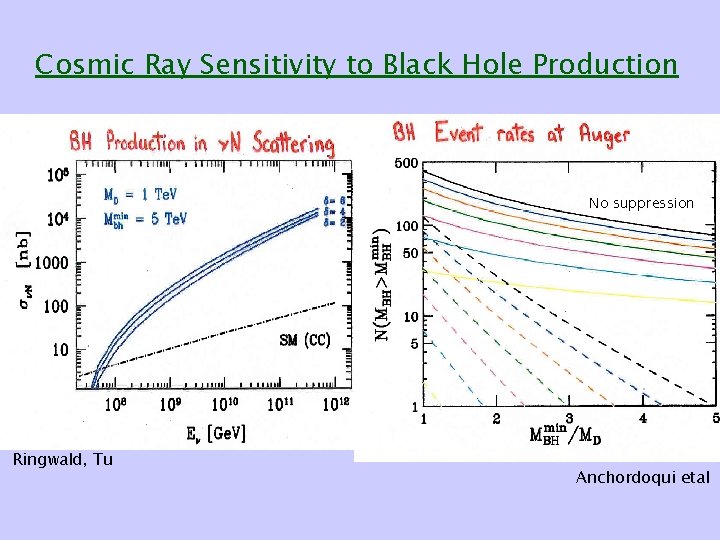
Cosmic Ray Sensitivity to Black Hole Production No suppression Ringwald, Tu Anchordoqui etal

Summary of Exp’t Constraints on MD Anchordoqui, Feng Goldberg, Shapere