External Storage For large data sets the computer

  • Slides: 10
Download presentation
External Storage • For large data sets, the computer will have to access the

External Storage • For large data sets, the computer will have to access the disk. • Disk access can take 200, 000 times longer than a machine instruction. • The RAM model does not account for disk I/O. memory 128 MB fast, expensive 60 GB slow, cheap disk Oct 29, 2001 CSE 373, Autumn 2001 1

Disks, continued • The difference between memory speed and disk speed is increasing. •

Disks, continued • The difference between memory speed and disk speed is increasing. • Example: State of Florida driving records (256 bytes). 10, 000 items. 6 disk accesses per second on a time-sharing system. • unbalanced binary search tree: possibly 10, 000 accesses. • BST: on avg. 32 accesses (5 sec. ) • AVL: worst: 1. 44 log n typical case: log n, 25 accesses (4 sec. ) Oct 29, 2001 CSE 373, Autumn 2001 2

Disk accesses • Goal: reduce the number of disk accesses. • We are willing

Disk accesses • Goal: reduce the number of disk accesses. • We are willing to do more complicated computations in memory in order to save disk time. • Idea: increase the branching of the tree so that the height is decreased. • Defn: An M-ary search tree allows up to M children per node. Oct 29, 2001 CSE 373, Autumn 2001 3

B-Trees 1. All the data items are stored at the leaves. 2. The non-leaf

B-Trees 1. All the data items are stored at the leaves. 2. The non-leaf nodes store up to M-1 keys. The ith key represents the smallest key in subtree i+1. 3. The root is either a leaf of has between 2 and M children. 4. All non-leaf nodes (except the root) have between M/2 and M children. 5. All leaves are at the same depth and have between L/2 and L data items. Oct 29, 2001 CSE 373, Autumn 2001 4

B-Trees: Choices • Choose M and L based on the size of the keys

B-Trees: Choices • Choose M and L based on the size of the keys K and on the size of the record R. • Suppose a disk block is of size B (bytes). Choose M so that a non-leaf node fits into one block: B (M-1) · K + M · 4 • Choose L so that a leaf node fits into one block: B L·R • accesses: log 2 N vs. log M/2 N Oct 29, 2001 CSE 373, Autumn 2001 5

Hash Tables • Constant time accesses! • A hash table is an array of

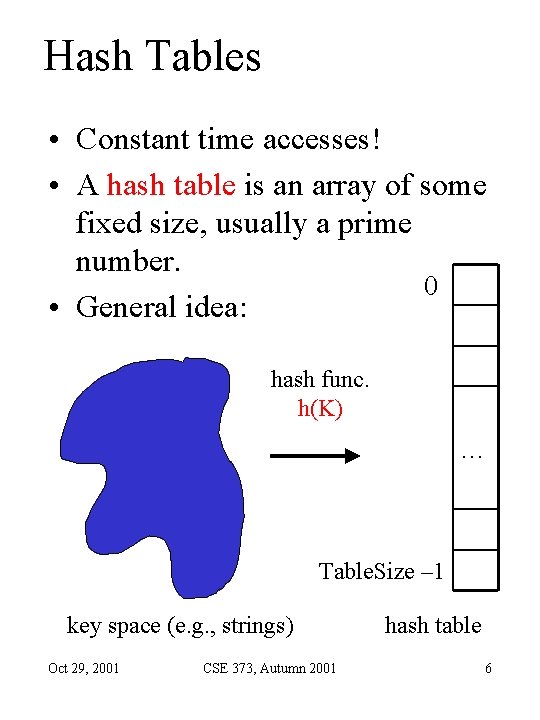
Hash Tables • Constant time accesses! • A hash table is an array of some fixed size, usually a prime number. 0 • General idea: hash func. h(K) … Table. Size – 1 key space (e. g. , strings) Oct 29, 2001 CSE 373, Autumn 2001 hash table 6

Desirable Properties We want a hash function to: 1. be simple/fast to compute, 2.

Desirable Properties We want a hash function to: 1. be simple/fast to compute, 2. map different keys to different cells, (impossible – why? ) 3. have keys distributed evenly among cells. Idea: If #1 and #3 are true and the hash table is not very full, then it should be fast to do a find. Oct 29, 2001 CSE 373, Autumn 2001 7

Example • key space = integers • h(K) = K mod 10 0 1

Example • key space = integers • h(K) = K mod 10 0 1 2 3 4 5 6 7 8 9 Oct 29, 2001 41 34 7 18 We lose all ordering information: find. Min, find. Max, inorder traversal, printing items in sorted order. CSE 373, Autumn 2001 8

Example 2 • key space = strings • s = s 0 s 1

Example 2 • key space = strings • s = s 0 s 1 s 2 … s k-1 h(s) = s 0 mod Table. Size BAD HASH FUNCTION h(s) = mod Table. Size BETTER HASH FUNCTION Oct 29, 2001 CSE 373, Autumn 2001 9

Collision Resolution • Separate chaining: All keys that map to the same hash value

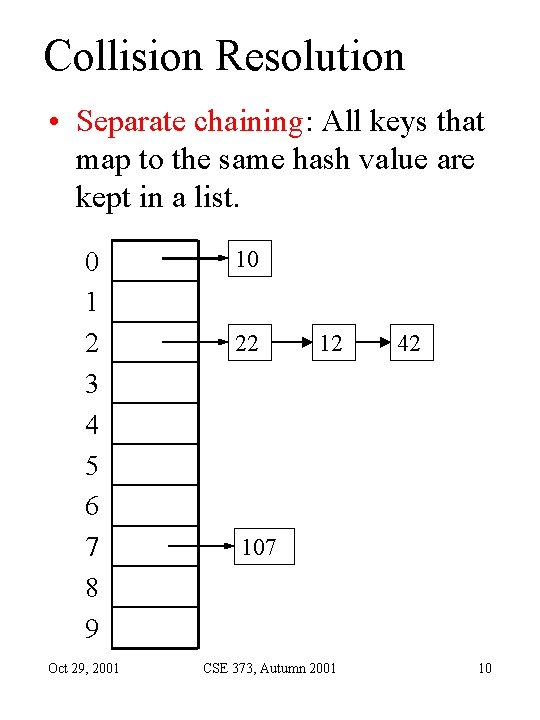
Collision Resolution • Separate chaining: All keys that map to the same hash value are kept in a list. 0 1 2 3 4 5 6 7 8 9 Oct 29, 2001 10 22 12 42 107 CSE 373, Autumn 2001 10