External Sorting 1 Why Sort A classic problem

External Sorting 1

Why Sort? A classic problem in computer science! v Data requested in sorted order v § e. g. , find students in increasing gpa order Sorting is first step in bulk loading B+ tree index. v Sorting useful for eliminating duplicate copies in a collection of records v Sort-merge join algorithm involves sorting. v v Problem: sort 10 GB of data with 1 MB of RAM. 2

Using secondary storage effectively v General Wisdom : § I/O costs dominate § Design algorithms to reduce I/O 3

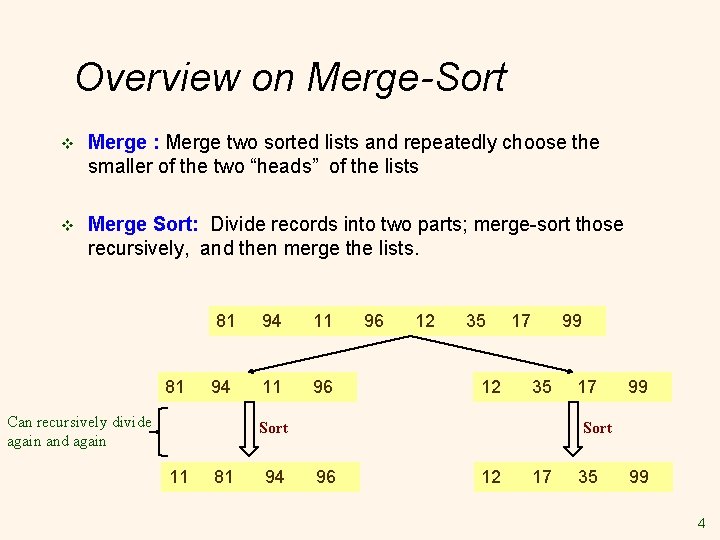
Overview on Merge-Sort v Merge : Merge two sorted lists and repeatedly choose the smaller of the two “heads” of the lists v Merge Sort: Divide records into two parts; merge-sort those recursively, and then merge the lists. 81 81 94 Can recursively divide again and again 94 11 11 96 96 12 35 12 17 99 35 Sort 11 81 94 17 99 Sort 96 12 17 35 99 4

Overview on Merge-Sort (Cont’d) v Merge : Merge two sorted lists and repeatedly choose the smaller of the two “heads” of the lists 81 81 94 Can recursively divide again and again 94 11 11 96 96 12 35 17 12 99 35 Sort 11 81 94 17 99 Sort 96 12 17 35 99 Merge 11 12 17 35 81 94 96 99 5

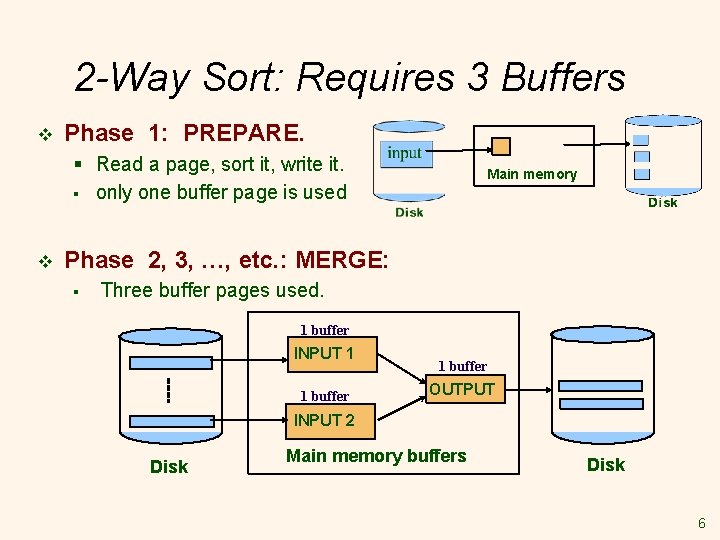
2 -Way Sort: Requires 3 Buffers v Phase 1: PREPARE. § Read a page, sort it, write it. § only one buffer page is used v Main memory Phase 2, 3, …, etc. : MERGE: § Three buffer pages used. 1 buffer INPUT 1 1 buffer OUTPUT INPUT 2 Disk Main memory buffers Disk 6

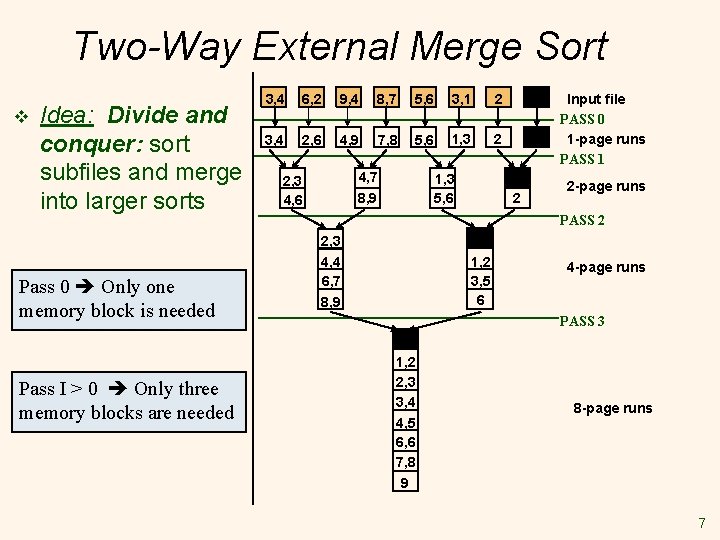
Two-Way External Merge Sort v Idea: Divide and conquer: sort subfiles and merge into larger sorts 3, 4 6, 2 9, 4 8, 7 5, 6 3, 1 2 3, 4 2, 6 4, 9 7, 8 5, 6 1, 3 2 4, 7 8, 9 2, 3 4, 6 1, 3 5, 6 Input file PASS 0 1 -page runs PASS 1 2 2 -page runs PASS 2 2, 3 Pass 0 Only one memory block is needed Pass I > 0 Only three memory blocks are needed 4, 4 6, 7 8, 9 1, 2 3, 5 6 4 -page runs PASS 3 1, 2 2, 3 3, 4 4, 5 6, 6 7, 8 9 8 -page runs 7

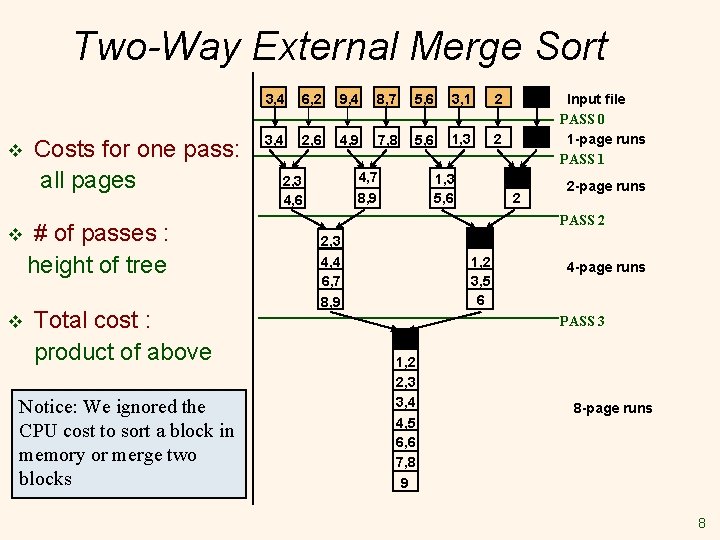
Two-Way External Merge Sort v v v Costs for one pass: all pages # of passes : height of tree Total cost : product of above Notice: We ignored the CPU cost to sort a block in memory or merge two blocks 3, 4 6, 2 9, 4 8, 7 5, 6 3, 1 2 3, 4 2, 6 4, 9 7, 8 5, 6 1, 3 2 4, 7 8, 9 2, 3 4, 6 1, 3 5, 6 Input file PASS 0 1 -page runs PASS 1 2 2 -page runs PASS 2 2, 3 4, 4 6, 7 8, 9 1, 2 3, 5 6 4 -page runs PASS 3 1, 2 2, 3 3, 4 4, 5 6, 6 7, 8 9 8 -page runs 8

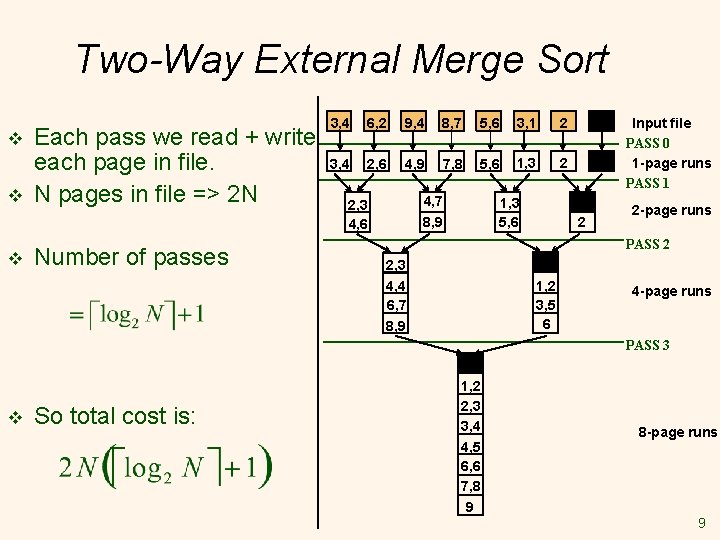
Two-Way External Merge Sort v v v Each pass we read + write each page in file. N pages in file => 2 N Number of passes 3, 4 6, 2 9, 4 8, 7 5, 6 3, 1 2 3, 4 2, 6 4, 9 7, 8 5, 6 1, 3 2 4, 7 8, 9 2, 3 4, 6 1, 3 5, 6 Input file PASS 0 1 -page runs PASS 1 2 2 -page runs PASS 2 2, 3 4, 4 6, 7 8, 9 1, 2 3, 5 6 4 -page runs PASS 3 v So total cost is: 1, 2 2, 3 3, 4 4, 5 6, 6 7, 8 9 8 -page runs 9

External Merge Sort What if we had more buffer pages? v How do we utilize them wisely ? v - Two main ideas ! 10

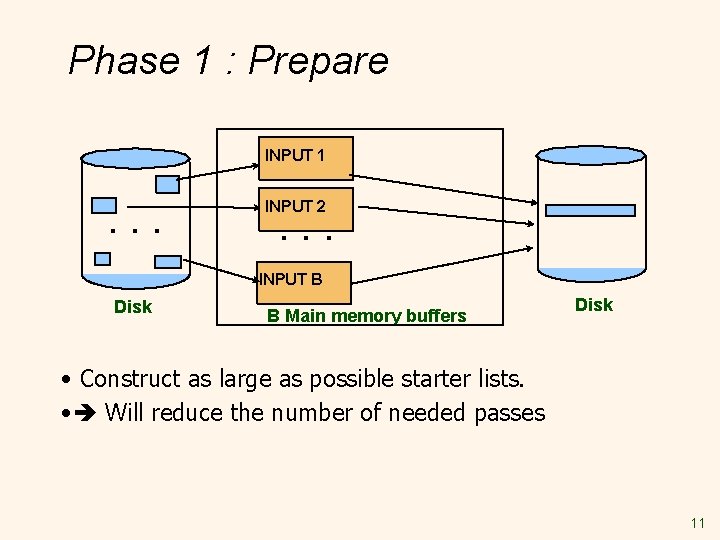
Phase 1 : Prepare INPUT 1 . . . INPUT 2 . . . INPUT B Disk B Main memory buffers Disk • Construct as large as possible starter lists. • Will reduce the number of needed passes 11

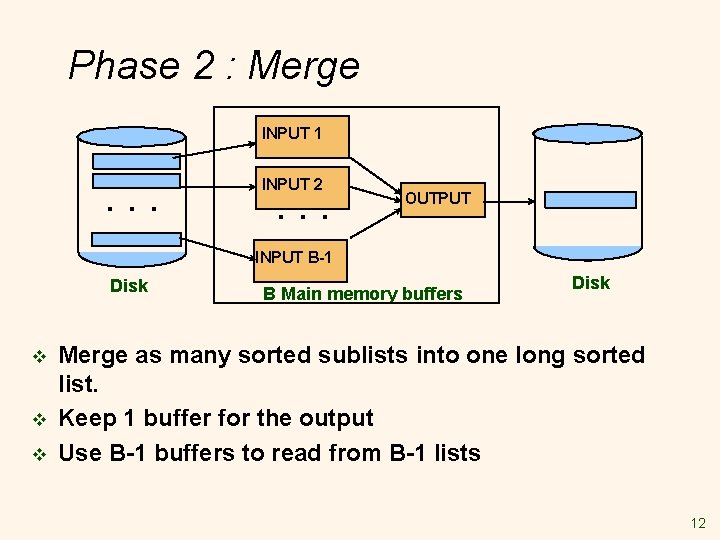
Phase 2 : Merge INPUT 1 . . . INPUT 2 . . . OUTPUT INPUT B-1 Disk v v v B Main memory buffers Disk Merge as many sorted sublists into one long sorted list. Keep 1 buffer for the output Use B-1 buffers to read from B-1 lists 12

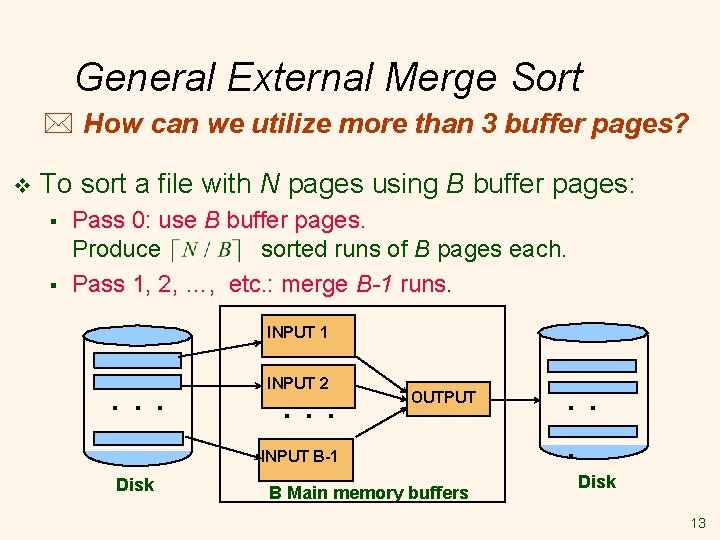
General External Merge Sort * How can we utilize more than 3 buffer pages? v To sort a file with N pages using B buffer pages: § § Pass 0: use B buffer pages. Produce sorted runs of B pages each. Pass 1, 2, …, etc. : merge B-1 runs. INPUT 1 . . . INPUT 2 . . . OUTPUT INPUT B-1 Disk B Main memory buffers . . . Disk 13

Cost of External Merge Sort Number of passes: v Cost = 2 N * (# of passes) v 14

Example v v Buffer : with 5 buffer pages File to sort : 108 pages § Pass 0: • Size of each run? • Number of runs? § Pass 1: • Size of each run? • Number of runs? § Pass 2: ? ? ? 15

Example Buffer : with 5 buffer pages v File to sort : 108 pages v § § Pass 0: = 22 sorted runs of 5 pages each (last run is only 3 pages) Pass 1: = 6 sorted runs of 20 pages each (last run is only 8 pages) Pass 2: 2 sorted runs, 80 pages and 28 pages Pass 3: Sorted file of 108 pages • Total I/O costs: ? 16

Example Buffer : with 5 buffer pages v File to sort : 108 pages v § § Pass 0: = 22 sorted runs of 5 pages each (last run is only 3 pages) Pass 1: = 6 sorted runs of 20 pages each (last run is only 8 pages) Pass 2: 2 sorted runs, 80 pages and 28 pages Pass 3: Sorted file of 108 pages • Total I/O costs: 2*N * (4 passes) 17

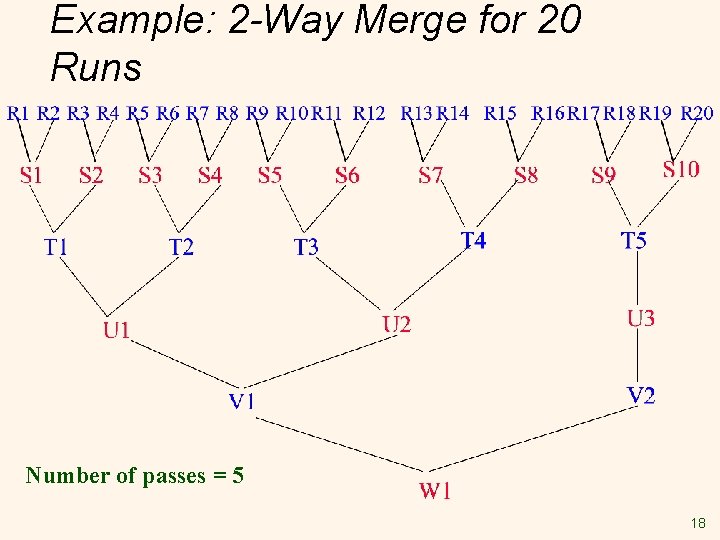
Example: 2 -Way Merge for 20 Runs Number of passes = 5 18

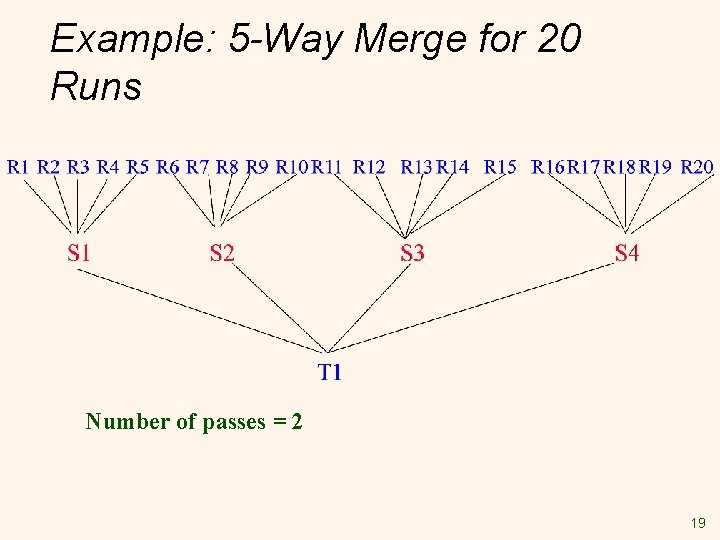
Example: 5 -Way Merge for 20 Runs Number of passes = 2 19

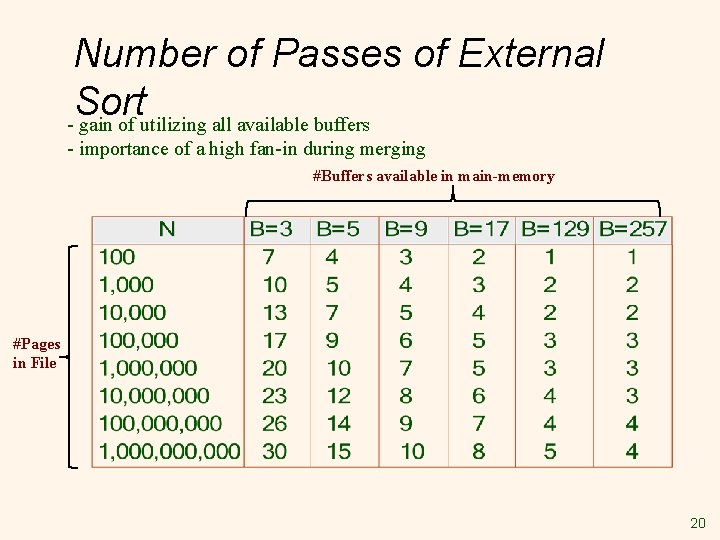
Number of Passes of External Sort - gain of utilizing all available buffers - importance of a high fan-in during merging #Buffers available in main-memory #Pages in File 20

Optimizing External Sorting v Cost metric ? § I/O only (till now) § CPU is nontrivial, worth reducing 21

Internal Main-Memory Sorting v Quicksort is a fast way to sort in memory. v An alternative is “heapsort” 22

Optimizing External Sorting v Further optimization for external sorting. § Blocked I/O § Double buffering 23

Blocked I/O for External Merge Sort v So far : 1 I/O one disk block to one memory buffer v Reading a several disk blocks sequentially is cheaper! v Suggests we should make each memory buffer (input/output) to hold several of disk blocks. § § But this will reduce fan-out during merge passes! In practice, most files still sorted in 2 -3 passes. 24

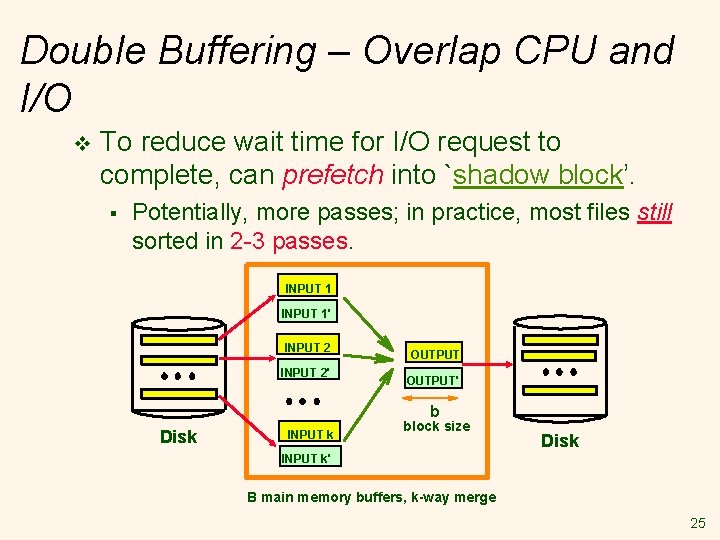
Double Buffering – Overlap CPU and I/O v To reduce wait time for I/O request to complete, can prefetch into `shadow block’. § Potentially, more passes; in practice, most files still sorted in 2 -3 passes. INPUT 1' INPUT 2' OUTPUT' b Disk INPUT k block size Disk INPUT k' B main memory buffers, k-way merge 25

Summary External sorting is important; DBMS may dedicate part of buffer pool for sorting! v External merge sort minimizes disk I/O costs: v § Two-Way External Sorting • § Only 3 memory buffers are needed Multi-Way External Sorting • Depends on the number of memory buffers available 26

Summary (Cont’d) v External merge sort minimizes disk I/O costs: § § § Pass 0: Produces sorted runs of size B (# buffer pages). Later passes: merge runs. # of runs merged at a time depends on B, and block size. Larger block size means less I/O cost per page. Larger block size means smaller # runs merged. In practice, # of runs rarely more than 2 or 3. 27

Summary (Cont’d) v Choice of internal sort algorithm may matter. v The best sorts are wildly fast: § Quick & Heap sorts 28