External Memory Graph Algorithms and Applications to GIS

External Memory Graph Algorithms and Applications to GIS Laura Toma Duke University July 14 2003 2/13/2022

Massive Data • Massive datasets are being collected everywhere • Storage management software is billion-$ industry Examples: § Geography: NASA satellites generate 1. 2 TB per day § WEB: Web crawl of 200 M pages and 2000 M links, Akamai stores 7 billion clicks per day § Phone: AT&T 20 TB phone call database § Consumer: Wal. Mart 70 TB database, buying patterns (supermarket checkout)

I/O Model [AV’ 88] Block I/O M § I/O-operation: • movement of one block of data from/to disk § Complexity measure: number of I/Os § Fundamental bounds: Scanning: scan(N) = N = problem size B = disk block size M = memory size Sorting: sort(N) = § In practice B and M are big I/Os

Outline § I/O-efficient graph algorithms • Problems, techniques and results § Algorithms for planar graphs using graph separation § A GIS application: Terra. Flow

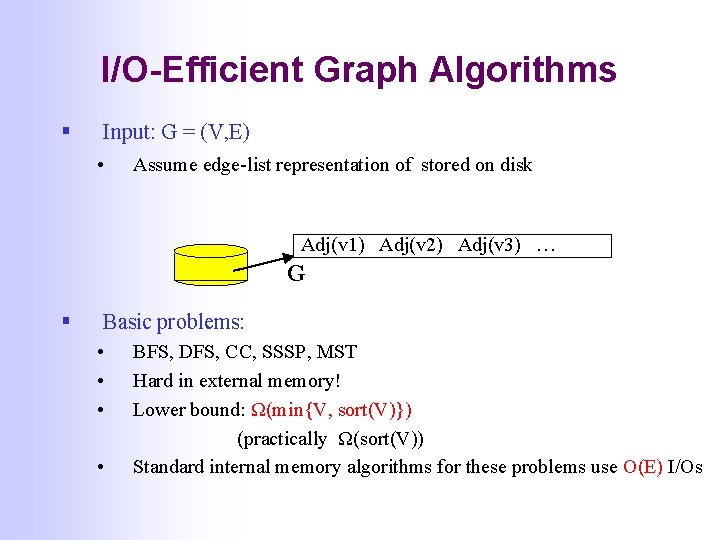
I/O-Efficient Graph Algorithms § Input: G = (V, E) • Assume edge-list representation of stored on disk Adj(v 1) Adj(v 2) Adj(v 3) … G § Basic problems: • • BFS, DFS, CC, SSSP, MST Hard in external memory! Lower bound: Ω(min{V, sort(V)}) (practically Ω(sort(V)) Standard internal memory algorithms for these problems use O(E) I/Os

BFS and DFS(u) § Mark u § For every v in Adj(u) • If v not marked DFS(v) Internal memory: O(V+E) External memory: § one I/O per vertex to load adjacency list Ω (V ) I/Os § one I/O per edge to check if v is marked Ω (E) I/Os O(V+E)= O(E) I/Os

SSSP and MST § Dijkstra’s algorithm • Maintain p-queue on vertices not yet included in SSSP • Repeatedly • Delete. Min(v) and relax each adjacent edge (v, u) if d(s, u) > d(s, u) + wvu then Decrease. Key(u, d(s, u) + wvu) v § External memory: • one I/O per vertex to load adjacency list Ω (V) I/Os • External p-queue: O(E) Insert/Delete. Min in O(sort(E)) I/Os • Decrease. Key: O(1) I/Os to read key of u Ω (E) I/Os O(V+E+sort(E))= O(E) I/Os

I/O-Efficient Graph Algorithms § Problems: 1. Random (unstructured) accesses to the adjacency lists of vertices as they are visited Ω(V) I/Os 2. Need to check if v has been already visited and/or read its key Ω(E) I/Os • • o(E) algorithm: solve (2) o(V) algorithm: solve (1) and (2)

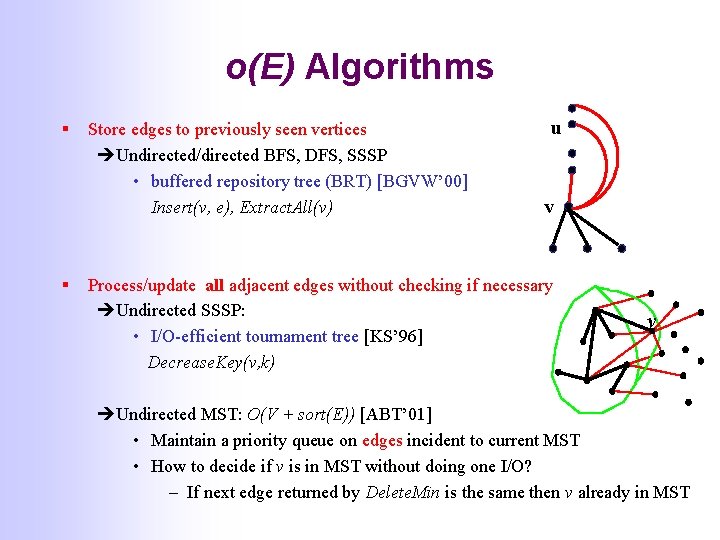
o(E) Algorithms § § Store edges to previously seen vertices Undirected/directed BFS, DFS, SSSP • buffered repository tree (BRT) [BGVW’ 00] Insert(v, e), Extract. All(v) u v Process/update all adjacent edges without checking if necessary Undirected SSSP: • I/O-efficient tournament tree [KS’ 96] Decrease. Key(v, k) v Undirected MST: O(V + sort(E)) [ABT’ 01] • Maintain a priority queue on edges incident to current MST • How to decide if v is in MST without doing one I/O? – If next edge returned by Delete. Min is the same then v already in MST

o(V) Algorithms § CC and MST: [MR’ 99, ABT’ 01] • graph contraction u 1 u 3 u 2 u 4 u 2 • Goal: reduce the problem to the same problem on a smaller graph by selecting disjoint subgraphs and contracting them • A contraction phase reduces nb of vertices by a constant fraction • Typically use a sequence of contraction steps G = G 0 G 1 G 2 … Gi … • CC and MST algorithms: general idea • Use contraction steps • Use an O(V+sort(E)) algorithm on G’

o(V) Algorithms • Undirected BFS, SSSP [MM’ 02, MZ’ 03] • Clustering • partition graph into V/k subgraphs (clusters) of k vertices • BFS Idea: Keep a pool of hot clusters • A cluster is loaded in the pool once • A cluster stays in the pool until all its vertices have been visited •

Upper Bounds § General undirected graphs • CC, MST: [MR’ 99, ABT’ 01] • BFS: [MM’ 02] • SSSP: [MZ’ 03] • DFS: [KS’ 96] § General directed graphs • BFS, DFS, SSSP: Topological sort [BVWB’ 00]

Upper Bounds Sparse Graphs § Sparse graphs E=O(V) • CC, MST: O(sort(V)) if graph stays sparse under edge contraction • Undirected BFS: O(sort(V)) ? open • Undirected SSSP: O(sort(V)) ? open • Undirected DFS: O(V) Directed BFS, DFS, SSSP o(V) ? open § O(sort(N)) BFS, SSSP, (DFS) on special classes of sparse graphs • Planar • Outerplanar, grid, bounded-treewidth

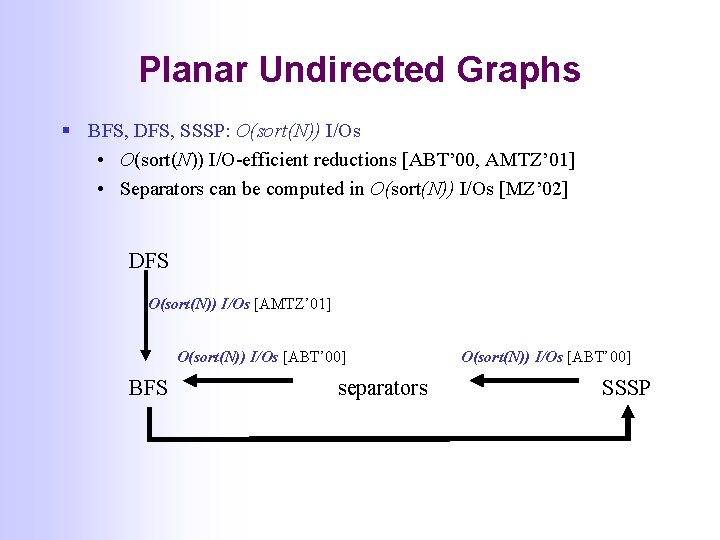
Planar Undirected Graphs § BFS, DFS, SSSP: O(sort(N)) I/Os • O(sort(N)) I/O-efficient reductions [ABT’ 00, AMTZ’ 01] • Separators can be computed in O(sort(N)) I/Os [MZ’ 02] DFS O(sort(N)) I/Os [AMTZ’ 01] O(sort(N)) I/Os [ABT’ 00] BFS separators O(sort(N)) I/Os [ABT’ 00] SSSP

I/O-Efficient Graph Algorithms Our Contributions § § § An MST on general undirected graphs. O(sort(N)) algorithms on planar graphs • Reducibility on planar undirected graphs • Planar digraphs: SSSP, BFS, directed ear decomposition and topological sort An O(sort(N) log N) DFS algorithm for planar undirected graphs • O(sort(N)) cycle separator All-pair-shortest-paths and diameter • Planar digraphs • General undirected graphs Data structure for shortest path queries on planar digraphs • Trade-off space-query GIS application: Terra. Flow • Flow modeling on grid terrains • r. terraflow: Port into GRASS, the open source GIS

Outline § I/O-efficient graph algorithms • Problems, techniques and results § Algorithms for planar graphs using graph separation • • Shortest paths (SSSP, BFS, APSP) DFS Topological sort on planar DAGs Data structure for SP queries § A GIS application: Terra. Flow

Planar graph separation: R-division § A partition of a planar graph using a set S of separator vertices into. subgraphs (clusters) Gi of at most R vertices each such that: • There are separators vertices in total • There is no edge between a vertex in Gi and a vertex in Gj • Each cluster is adjacent to separator vertices R R R R R

R-division § Boundary vertices Bnd(Gi) of Gi • The separator vertices adjacent to Gi § Boundary set • Maximal subset of separator vertices that are adjacent to the same clusters § Lemma [Frederickson’ 87]: • R-division of a planar graph of bounded degree has boundary sets.

R-divisions and Planar Graph Algorithms § R-divisions [Frederickson’ 87] dynamic graph algorithms [GI’ 91, KS’ 93], faster SP algorithms [HKRS’ 97], SP data structures § In external memory choose R = B 2 • O(N/B) separator vertices • O(N/B 2) clusters of O(B 2) vertices each and O(B) boundary vertices • O(N/B 2) boundary sets • Can be computed in O(sort(N)) I/Os [MZ’ 02] § B 2 -division SSSP, BFS, DFS, topological sort, APSP, diameter, SP data structures, . .

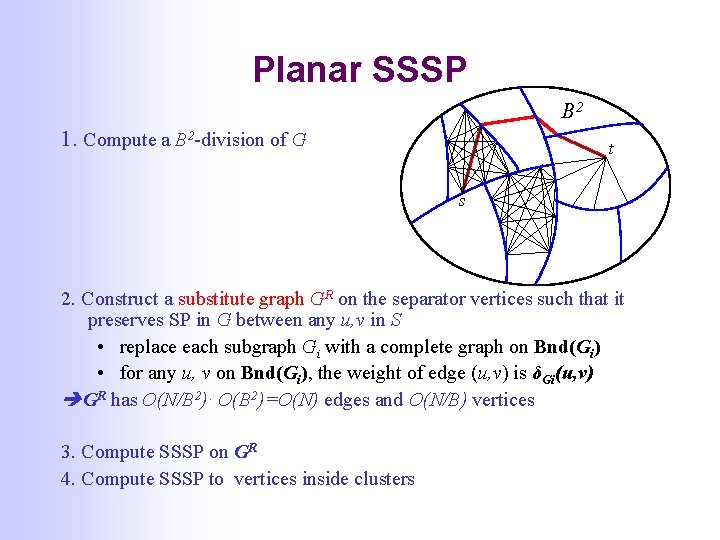
Planar SSSP B 2 1. Compute a B 2 -division of G t s 2. Construct a substitute graph GR on the separator vertices such that it preserves SP in G between any u, v in S • replace each subgraph Gi with a complete graph on Bnd(Gi) • for any u, v on Bnd(Gi), the weight of edge (u, v) is δGi(u, v) GR has O(N/B 2)· O(B 2)=O(N) edges and O(N/B) vertices 3. Compute SSSP on GR 4. Compute SSSP to vertices inside clusters

Planar SSSP on GR with O(N/B) vertices and O(N) edges § Dijkstra’s algorithm with I/O-efficient p-queue • Access to adjacency list of each vertex takes O(N/B) I/Os • O(N) Insert/Delete. Min in O(sort(N)) I/Os [A 95] • But. . need dist(s, u) for all u in Adj(v) v § Keep list LS={dist(s, u), for any u in S} • For each vertex v read from LS the current distances of adjacent vertices O(N) edges => O(N) accesses to LS O(N) I/Os

Planar SSSP on GR Idea: use boundary sets Store LS so that vertices in the same boundary set are consecutive • There are O(N/B 2) boundary sets • Vertices in same boundary set have same O(B) neighbors in GR assuming G has bounded degree • Each boundary set is accessed once by each neighbor in GR • Each boundary set has size O(B) O(N/B 2) x O(B) = O(N/B) I/Os

Planar APSP § § § Straightforward bound: O(N sort(N)) = O(sort(N 2)) Improved to optimal O(scan(N 2)) Idea: compute SP from all vertices in a cluster while cluster is in memory § For each cluster Gi § For any α in Bnd(Gi) compute SSSP(α) in GR § For each cluster Gj § load in memory Gj, Bnd(Gj) and δ(Bnd(Gi), Bnd(Gj)) § compute the shortest paths between all vertices in Gi and Gj d(u, v)=min{δGj (u, α) + δGR(α, β) + δGi(β, v) | α in Bnd(Gi), β in Bnd(Gj)} α u G § v β G j § write the output i O(N/B 2) clusters O(sort(N 2)/B) [compute] + O(scan(N 2)) [output] Diameter: O(sort(N 2)/B)

General AP-BFS The APSP idea (compute SP from all vertices of a cluster while the cluster is in main memory) can be generalized to other algorithms which use clustering, like the BFS algorithm [MM’ 02] on general undirected graphs. Theorem: • AP-BFS of a general undirected graph and its unweighted diameter can be computed in O(V sort(E)) I/Os. Note: • general undirected BFS is O(sort(E)) amortized over V vertices

Planar DFS Idea: Partition the faces of G into levels around a source face containing s and grow DFS level-by-level • Levels can be obtained from BFS in dual graph • Structure of levels is simple (bicomps are cycles) • Rooting/Attaching: use that a spanning tree is a DFS-tree if and only if it has no cross edges A DFS-tree of a planar graph can be computed in O(sort(N)) I/Os

Planar Graphs § Shortest paths • generalize to digraphs: compute B 2 -division on the underlying graph • BFS, SSSP in O(sort(N)) • APSP (transitive closure) in O(scan(N 2)) • diameter in O(sort(N 2)/B) § DFS • Undirected • O(sort(N)) using BFS in the dual [O(sort(N) log N) direct algorithm using cycle separators] • Directed • The planar undirected DFS algorithms do not extend to digraphs • O(sort(N)) DFS? open

Outline § I/O-efficient graph algorithms • Problems, techniques and results § Algorithms for planar graphs using graph separation • Shortest paths (SSSP, BFS, APSP) • DFS • Topological sort on planar DAGs • O(sort(N)) using directed ear decomposition (DED) of its dual • Simplified algorithm using B 2 -division • Data structure for SP queries § A GIS application: Terra. Flow

Directed Ear Decomposition (DED) § A directed ear decomposition of a graph G is a partition of G into simple directed paths P 0, P 1, …, Pk such that: • P 0 is a simple cycle • endpoints of each Pi i>0 are in lower-indexed paths Pj, Pl, j, l<i • internal vertices of each Pi i>0 are not in any Pj j<i § G has a directed ear decomposition if and only if it is strongly connected (exist directed cycle containing each pair of vertices u, v). § Planar DED: O(sort(N)) I/Os

Planar Topological Sort using DED § Theorem [KK’ 79]: The directed dual of a planar DAG is strongly connected and therefore has a directed ear decomposition. § Idea: • Place vertices to the left of P 0 before vertices to the right • Sort two sets recursively § Used in PRAM topological sort algorithm [KK 93, K 93] § PRAM simulation O(sort(N)log N) I/Os § Improved to O(sort(N)) by defining and utilizing ordered ear decomposition tree [ATZ’ 03]

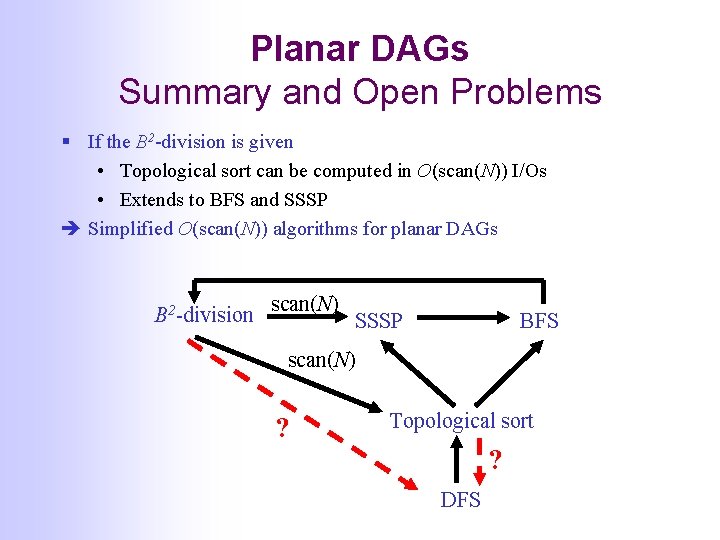
O(sort(N)) Topological Sort using B 2 -division Same idea as in planar SSSP algorithm § Construct a substitute graph GR using B 2 -division • edge from v to u on boundary of Gi if exists path from v to u in Gi § Topologically sort GR (separator vertices in G): • Store in-degree of each vertex in list L • Maintain list of in-degree zero vertices • Repeatedly: • Number an in-degree zero vertex v • Consider all edges (v, u) and decrement in-degree of u in L analysis exactly as in SSSP algorithm O(scan(N)) if B 2 -division is given B 2 v

O(sort(N)) Topological Sort using B 2 -division § Problem: • Not clear how to incorporate removed vertices from G in topological order of separator vertices (GR) 5 A 1 E D F C 43 B 2 § Solution (assuming only one in-degree zero vertex s for simplicity): • Longest-path-from-s order is a topological order • Longest paths to removed vertices B 2 t locally computable from longest-paths to boundary vertices s

O(sort(N)) Topological Sort using B 2 -division 1. Compute a B 2 -division of G 2. Construct substitute graph GR using • Weight of edge between v and u on boundary of Gi equal to length of longest path from v to u in Gi 2. Compute longest path to each vertex in GR (same as in G): • Maintain list L of longest paths seen to each vertex • Repeatedly: • Obtain longest path for next v vertex v in topological order • Consider all edges (v, u) and update longest path to u 3. Find longest path to vertices inside clusters analysis exactly as for planar SSSP algorithm O(scan(N)) if B 2 -division is given

Outline § I/O-efficient graph algorithms • Problems, techniques and results § Algorithms for planar graphs using graph separation • • Shortest paths (SSSP, BFS, APSP) DFS Topological sort on planar DAGs Data structure for SP queries § A GIS application: Terra. Flow

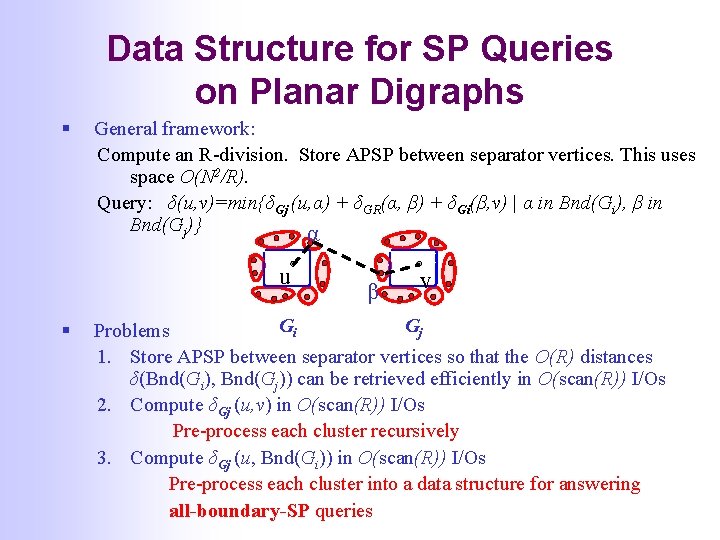
Data Structure for SP Queries on Planar Digraphs § Problem: pre-process a planar digraph into a data structure in order to answer efficiently distance (shortest path) queries between arbitrary vertices § Trade-off space-query: O(S) space, query = ? • The two extreme straightforward solutions: • O(N) space, O(sort(N)) I/O query • O(N 2) space, O(1) I/O query § Related work: • Planar graphs: [Arikati et al, Djidjev, 1996] [Chen & Xu, 2000] • Space-query trade-off: for any S in [N, N 2], S x Q = O(N 2) • General graphs: • approx shortest paths [Cohen, Halperin, Zwick, …] • I/O-model : space, query [HMZ’ 99]

Data Structure for SP Queries on Planar Digraphs § Basic data structure [Arikati et al, Djidjev]: • Recursively, compute a separator and store for each vertex u in G the shortest path from u to all separator vertices. Space , query time, I/Os [HMZ’ 99] § Generalized to any S in [N, N 2]: O(S) space, Q=O(N 2/S) • Use R-division • S in [N, N 3/2]: Store shortest paths between the separator vertices and compute shortest path in each cluster on the fly. • S in [N 3/2, N 2]: Pre-process each cluster as a basic data structure and for any vertex u in G store shortest paths from u to all separator vertices. § I/O-model • S in [N, N 3/2]: ? • S in [N 3/2, N 2]: O(S) space, query using [HMZ’ 99]

Data Structure for SP Queries on Planar Digraphs § General framework: Compute an R-division. Store APSP between separator vertices. This uses space O(N 2/R). Query: δ(u, v)=min{δGj (u, α) + δGR(α, β) + δGi(β, v) | α in Bnd(Gi), β in Bnd(Gj)} α u § β v Gi Gj Problems 1. Store APSP between separator vertices so that the O(R) distances δ(Bnd(Gi), Bnd(Gj)) can be retrieved efficiently in O(scan(R)) I/Os 2. Compute δGj (u, v) in O(scan(R)) I/Os Pre-process each cluster recursively 3. Compute δGj (u, Bnd(Gi)) in O(scan(R)) I/Os Pre-process each cluster into a data structure for answering all-boundary-SP queries

Data Structure for SP Queries on Planar Digraphs § Let G be a planar graph of size N and Bnd(G) its boundary of size O(N 1/2). There exists a data structure that uses space O(N lg N) and answers allboundary-shortest-path queries in O(N/B) I/Os. § Theorem: For any S in [N, N 2/B] there exists a data structure which answers distance queries in I/Os and can be built in I/Os. The size is. if and if. • For S = Θ(N): O(N log 2 N) space and O(N/B) query • For any S/N = Ω (Nε) or S = Ω (N 1 +ε) for some ε in (0, 1] There exists a data structure of size O(S) which answers distance queries in I/Os and can be built in I/Os.

Outline § I/O-efficient graph algorithms • Problems, techniques and results § Algorithms for planar graphs using graph separation • • Shortest paths DFS Topological sort on planar DAGs Data structure for SP queries § A GIS application: Terra. Flow

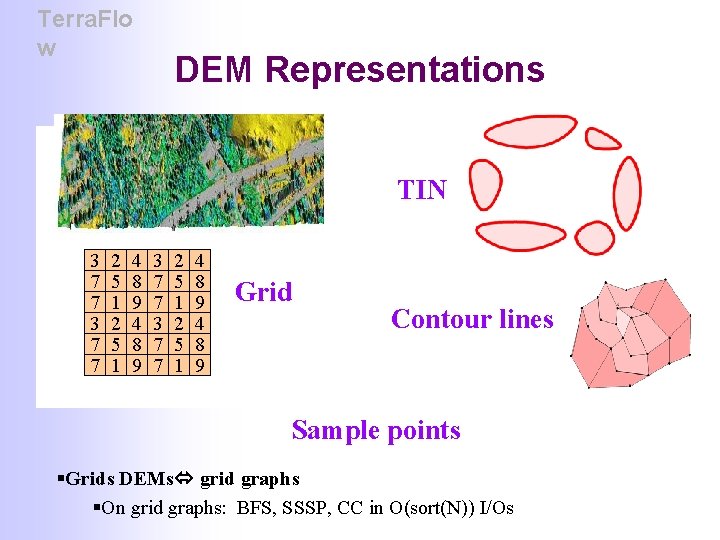
Terra. Flo w DEM Representations TIN 3 7 7 2 5 1 4 8 9 Grid Contour lines Sample points §Grids DEMs grid graphs §On grid graphs: BFS, SSSP, CC in O(sort(N)) I/Os

Terra. Flo w Example: LIDAR Terrain Data § Massive (irregular) point sets (1 -10 m resolution) § Relatively cheap and easy to collect Example: Jockey’s ridge (NC coast)

Terra. Flo w Modeling Flow on Terrains § What happens when it rains? • Predict areas susceptible to floods. • Predict location of streams. § Flow is modeled by computing two basic attributes from the DEM of the terrain: • Flow Direction (FD) • The direction water flows at a point • Flow Accumulation (FA) • Total amount of water that flows through a point if water is distributed according to the flow directions

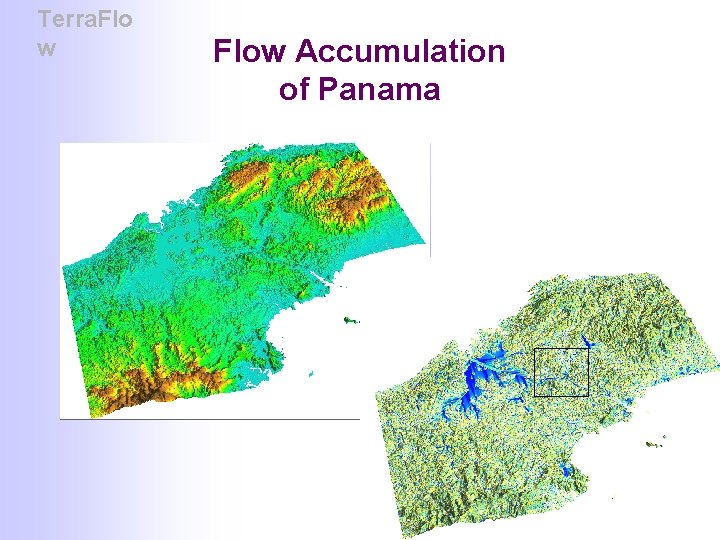
Terra. Flo w Flow Accumulation of Panama

Terra. Flo w Panama Flow Accumulation: zoom

Terra. Flo w GIS Performance on Massive Data § GRASS (open source GIS) • Killed after running for 17 days on a 6700 x 4300 grid (approx 50 MB dataset) § TARDEM (research, U. Utah) • Killed after running for 20 days on a 12000 x 10000 grid (appox 240 MB dataset) • CPU utilization 5%, 3 GB swap file § Arc. Info (commercial GIS) • Can handle the 240 MB dataset • Doesn’t work for datasets bigger than 2 GB

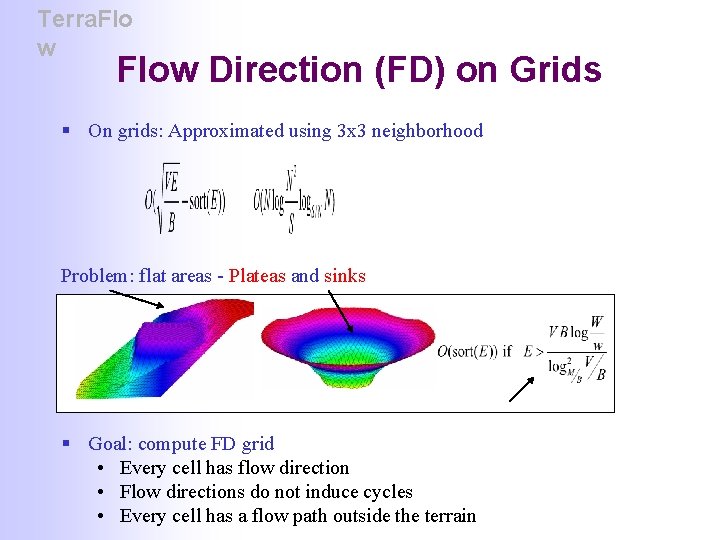
Terra. Flo w Flow Direction (FD) on Grids § On grids: Approximated using 3 x 3 neighborhood Problem: flat areas - Plateas and sinks § Goal: compute FD grid • Every cell has flow direction • Flow directions do not induce cycles • Every cell has a flow path outside the terrain

Terra. Flo w FD on Flat Areas § Plateaus • A cell flows towards the nearest spill point on the boundary of the plateau • Compute FD on plateaus using CC and BFS § Sinks • Route the water uphill out of the sink by modeling flooding: uniformly pouring water on terrain until steady-state is reached • Flooding removes (fills) sinks Assign uphill flow directions on the original terrain by assigning downhill flow directions on the flooded terrain

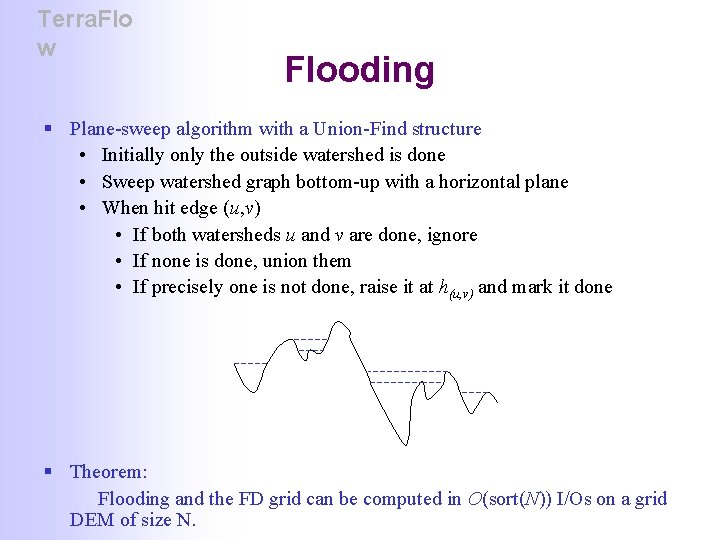
Terra. Flo w Flooding § Watershed: part of the terrain that flows into a sink § Sinks partition of terrain into watersheds watershed graph GT • Vertices are watersheds; add vertex for the “outside” watershed • Edge (u, v) if watersheds u, v are adjacent • Edge (u, v) labeled with lowest height on boundary between u and v § Flooding: Compute for each watershed u to the height hu of the lowestheight path in GT from u to the “outside” watershed. • the height of a path is the height of the highest edge on path

Terra. Flo w Flooding § Plane-sweep algorithm with a Union-Find structure • Initially only the outside watershed is done • Sweep watershed graph bottom-up with a horizontal plane • When hit edge (u, v) • If both watersheds u and v are done, ignore • If none is done, union them • If precisely one is not done, raise it at h(u, v) and mark it done § Theorem: Flooding and the FD grid can be computed in O(sort(N)) I/Os on a grid DEM of size N.

Terra. Flo w Flow Accumulation (FA) on Grids FA models water amount of flow through each cell with “uniform rain” • Initially one unit of water in each cell • Water distributed from each cell to neighbors pointed to by its FD • Flow conservation: If several FD, distribute proportionally to height difference • Flow accumulation of cell is total flow through it Goal: compute FA for every cell in the grid (FA grid) Theorem: The FA grid can be computed in O(sort(N)) I/Os.

Terra. Flo w http: //www. cs. duke. edu/geo*/terr Terra. Flow § Terra. Flow: implementation of I/O-efficient FD and FA algorithms • Significantly faster on very large grids than existing GIS software • Scalable: 1 billion elements!! (>2 GB data) • Allows multiple methods flow modeling § Implementation • C++, uses TPIE (Transparent Parallel I/O Environment) • Library of I/O-efficient modules developed at Duke § Experimental platform • Terra. Flow, Arc. Info: 500 MHz Alpha, Free. BSD 4. 0, 1 GB RAM • GRASS/TARDEM: 500 MHz Intel PIII, Free. BSD/Windows, 1 GB RAM

Terra. Flo w http: //www. cs. duke. edu/geo*/terr Terra. Flow § GRASS cannot handle Hawaii dataset (killed after 17 days) § TARDEM cannot handle Cumberlands dataset (killed after 20 days) § Significant speedup over Arc. Info (ESRI) for large datasets • East-Coast Terra. Flow: 8. 7 Hours Arc. Info: 78 Hours • Washington Terra. Flow: 63 Hours Arc. Info: %

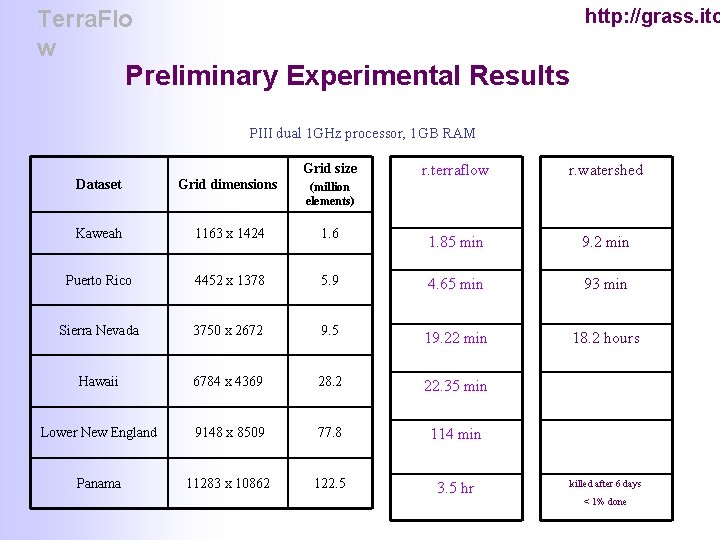
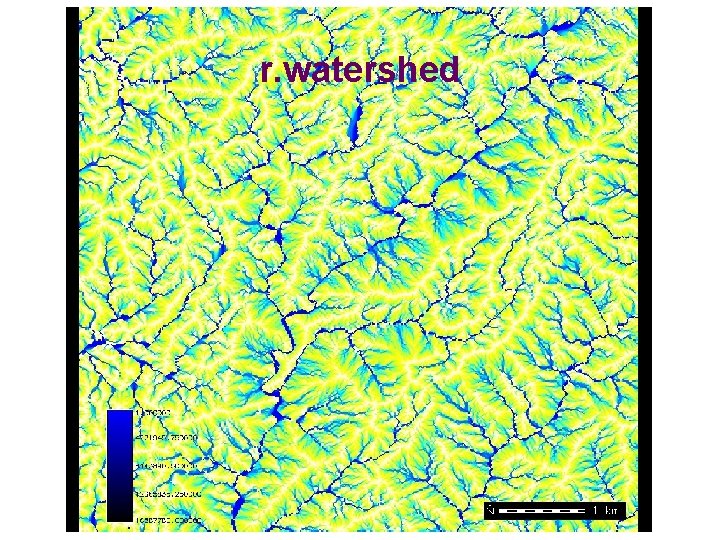
http: //grass. itc Terra. Flow in GRASS § r. terraflow • Port of Terra. Flow into GRASS • Available with GRASS 5. 0. 2 § Preliminary results on • Quality of output • Comparison with r. watershed • SFD, MFD comparison • Performance analysis § Good response from users

http: //grass. itc Terra. Flo w Preliminary Experimental Results PIII dual 1 GHz processor, 1 GB RAM Grid size r. terraflow r. watershed 1. 85 min 9. 2 min Dataset Grid dimensions (million elements) Kaweah 1163 x 1424 1. 6 Puerto Rico 4452 x 1378 5. 9 4. 65 min 93 min Sierra Nevada 3750 x 2672 9. 5 19. 22 min 18. 2 hours Hawaii 6784 x 4369 28. 2 22. 35 min Lower New England 9148 x 8509 77. 8 114 min Panama 11283 x 10862 122. 5 3. 5 hr killed after 6 days < 1% done

I/O-Efficient GIS Future Directions § Terra. Flow • Extend flow direction modeling (D-inf) • Realistic treatment of flat areas • Partial flooding • Computing complete watershed hierarchy § Processing LIDAR data • Point to grid conversion, point to TIN conversion, terrain simplification, Delaunay triangulation… § TINs • Practical algorithms on triangulations • Flow modeling on TINs • Geometric? Graph theoretical?

I/O-Efficient Graph Algorithms Open Problems § Improved algorithms for general digraphs § O(sort(N)) DFS on planar digraphs • Planar DAGs: can a DFS-tree be computed using topological order? § O(sort(E)) algorithm for CC/MST § Improved DFS on general undirected graphs (clustering? ) § Simple and feasible O(sort(N)) algorithms for planar graphs and in particular for triangulations § Dynamic data structures for planar graphs

The End

Upper Bounds General undirected graphs Dense graphs § CC, MST: : § BFS: Sparse graphs E=O(V) § CC, MST: O(sort(V)) if graph closed under edge contraction § BFS: § SSSP: § DFS: O(V) § DFS: § O(sort(V)) BFS, DFS, SSSP on planar graphs, outerplanar graphs, grid graphs, bounded-tree-width graphs

MST Contraction Step § § Used in PRAM MST algorithms [CLC’ 82] Each vertex selects its lightest adjacent edge Lemma: Each selected edge must be part of MST The selected edges are contracted: • Number of resulting vertices at most V/2 • Note: contraction does not reduce the number of edges § MST contraction step in O(sort(E)) I/Os • Finding the representative of a super-vertex [ABT’ 01]

I/O-Efficient MST • Graph contraction algorithm can be improved by grouping the contraction steps in super-steps • Each super-step in O(sort(E) + sort(V)) I/Os • Basic idea: in order to perform k contraction steps need to know only the 2 k lightest edges adjacent to each node each super-step works with a subset of the edges {nb contraction steps} x {subset of edges} = O(V)

A direct O(sort(N) log N) DFS Algorithm on Planar Undirected Graphs § § Divide-and-conquer using cycle separators [PRAM DFS, Smith 86] Algorithm • Compute a cycle separator C and path P • Compute DFS recursively in the connected components Gi of GP • Attach the DFS trees of Gi onto the cycle § I/O-analysis • O(log N) recursive steps • O(sort(N)) I/Os per step • simple O(sort(N)) algorithm for finding a cycle separator O(sort(N) log N) I/Os in total

Planar DFS § § Denote • Gi = union of the boundaries of faces at level <= i • Hi = Gi G i-1 • Ti = DFS-tree of Gi Structure of levels is simple • The bicomps of the Hi are the boundary cycles of Gi

Planar DFS § Algorithm: Compute DFS of Hi and attach it onto Ti-1 § Attaching onto Ti-1 :

Planar DAGs Summary and Open Problems § If the B 2 -division is given • Topological sort can be computed in O(scan(N)) I/Os • Extends to BFS and SSSP Simplified O(scan(N)) algorithms for planar DAGs B 2 -division scan(N) SSSP BFS scan(N) ? Topological sort ? DFS

Terra. Flo w Massive Terrain Data § Remote sensing technology • Massive amounts of terrain data • Higher resolutions (1 km, 100 m, 30 m, 1 m, …) § NASA-SRTM • Mission launched in 2001 • Acquired data for 80% of earth at 30 m resolution • 5 TB § USGS • Most of US at 10 m resolution § LIDAR • 1 m res

Terra. Flo w Uses Flow direction and flow accumulation are used for: § Computing other hydrological attributes • river network • moisture indices • watersheds and watershed divides § Analysis and prediction of sediment and pollutant movement in landscapes. § Decision support in land management, flood and pollution prevention and disaster management

Terra. Flo w Standard FA Algorithm § Algorithm: • Input: flow direction grid FD • Output: flow accumulation grid FA (initialized to 1) • Process (sweep) cells in topological order. For each cell: • Read flow from FA grid and direction from FD grid • Update flow in FA grid for downslope neighbors § Analysis • One sweep enough: O(sort) + O(N) time for a grid of N cells, • . . but O(N) I/Os: Cells in topological order distributed over the terrain

Terra. Flo w I/O-Efficient FA Algorithm § Eliminating scattered accesses to FD grid • Store FD grid in topological order § Eliminating scattered accesses to FA grid. . …. by replacing them with accesses to a p-queue • Idea: Flow to neighbor is only needed when neighbor is processed • time when cell is processed topological rank priority • Push flow by Insert-ing a flow increment in p-queue with priority equal to neighbor’s time • Flow of cell obtained using Delete. Min • Note: Augment each cell with priorities of 8 neighbors • Obs: Space (~9 N) traded for I/O The FA grid can be computed in O(sort(N)) I/Os.

GRASS: >r. terraflow help Description: Flow computation for massive grids. Usage: r. terraflow [-sq] elev=name filled=name direction=name watershed=name accumulation=name tci=name [d 8 cut=value] [memory=value] [STREAM_DIR=name] [stats=name] Flags: -s SFD (D 8) flow (default is MFD) -q Quiet Parameters: elev filled direction watershed accumulation tci d 8 cut direction Input elevation grid Output (filled) elevation grid Output direction grid Output watershed grid Output accumulation grid Output tci grid If flow accumulation is larger than this value it is routed using SFD (D 8) (meaningfull only for MFD flow only). default: infinity memory Main memory size (in MB) default: 300 STREAM_DIR Location of intermediate STREAMs default: /var/tmp http: //www. cs. duke. edu/geo*/terr

Flat DEM

r. terraflow MFD

r. terraflow SFD

r. watershed

r. terraflow MFD zoom, 2 D

r. terraflow SFD zoom, 2 D

It’s Growing! § Appalachian Mountains Area if approx. 800 km x 800 km Sampled at: • 100 m resolution: 64 million points (128 MB) • 30 m resolution: 640 (1. 2 GB) • 10 m resolution: 6400 = 6. 4 billion (12 GB) • 1 m resolution: 600. 4 billion (1. 2 TB)