Extensions to the OSi L schema Matrix and

Extensions to the OSi. L schema: Matrix and cone programming Horand I. Gassmann, Dalhousie University Jun Ma, Kipp Martin, Imre Polik

Outline • Matrices and optimization • Optimization Services • OSi. L (Optimization Services instance Language) • Cone and matrix programming • Extensions to OSi. L – Matrices – Cones – Matrix programming • OS and CSDP © 2014 H. I. Gassmann

Matrices in optimization • Coefficient matrices in linear programming • Jacobian and Hessian matrices, gradient vectors • Matrix variables in positive semidefinite programming • Formats for sparse matrix representations – Harvard format (starts, indices and values) – MPS, CPLEX LP format – SDP format Static (real) values only, even SDP result format © 2014 H. I. Gassmann

Cone and matrix programming • Constraints (and objectives) expressed in terms of cones – – Second order cones Cones of positive semidefinite matrices Orthant cones (linear cones) Cones of nonnegative polynomials (over some interval) • Solvers: CSDP, Se. Du. Mi, Mosek, Cplex, Gurobi, FICO • Unified treatment within the Optimization Services framework © 2014 H. I. Gassmann

Sample problems • Second order cone program • Semidefinite program © 2014 H. I. Gassmann

CSDP • Open-source project (COIN-OR) • Solves • Assumes Ai, C, X are real and symmetric • : positive semidefinite © 2014 H. I. Gassmann

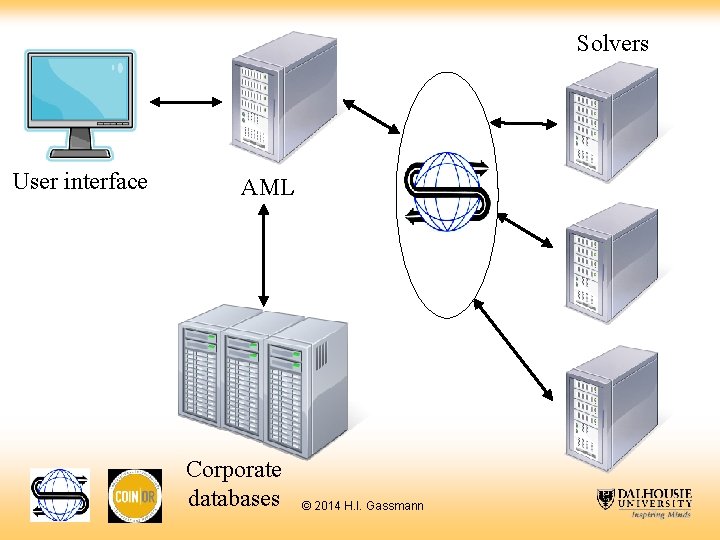
Optimization Services • Framework for optimization in a distributed computing environment • XML schemas for communicating instances, options, results, … • Implementation (COIN-OR project OS) – – OSSolver. Service OSAmpl. Client OSServer callable library © 2014 H. I. Gassmann

Solvers User interface AML Corporate databases Data interchange © 2014 H. I. Gassmann

“Core” OS and OSi. L • Problems handled – – – Linear programs Integer programs MILP Convex NLP Discrete NLP Nonconvex NLP • Available solvers – – – – – © 2014 H. I. Gassmann Clp Cbc SYMPHONY Ipopt Bonmin Couenne Glpk Cplex Gurobi Mosek

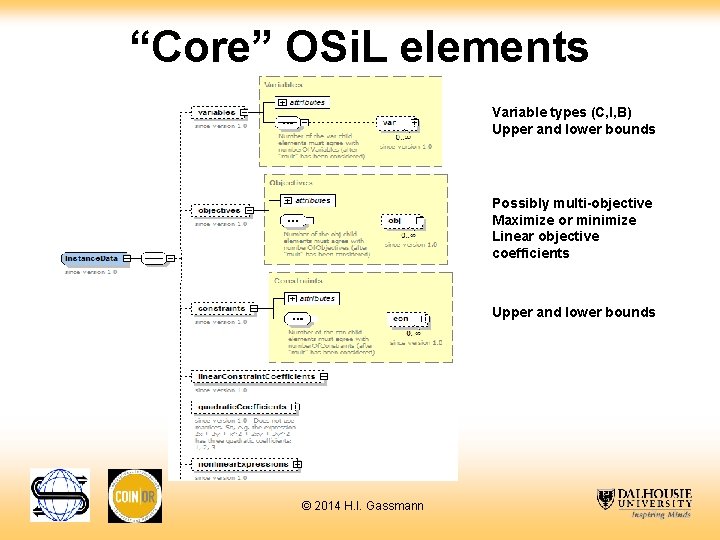
“Core” OSi. L elements Variable types (C, I, B) Upper and lower bounds Possibly multi-objective Maximize or minimize Linear objective coefficients Upper and lower bounds © 2014 H. I. Gassmann

Requirements and challenges • Cone inclusions, e. g. , – X is symmetric, positive semidefinite – Ax lies in the rotated quadratic cone RC(1, 2; 3. . n) • Matrix expressions, e. g. , – AXB + BXA – trace ATX • What does a linear matrix expression look like? © 2014 H. I. Gassmann

Design principles • • • Preserve core Be as general as possible Respect sparsity Avoid painting yourself into corners New constructs – <matrix> – <cone> – <matrix. Programming> © 2014 H. I. Gassmann

OSi. L and matrices • Constant matrices • Matrix variables X (or ? ) • General matrices (e. g. , Hessian, Jacobian, etc. ) • • • Symmetry Sparsity Block structure Matrix construction, e. g. , A = a a. T One matrix type or several? © 2014 H. I. Gassmann

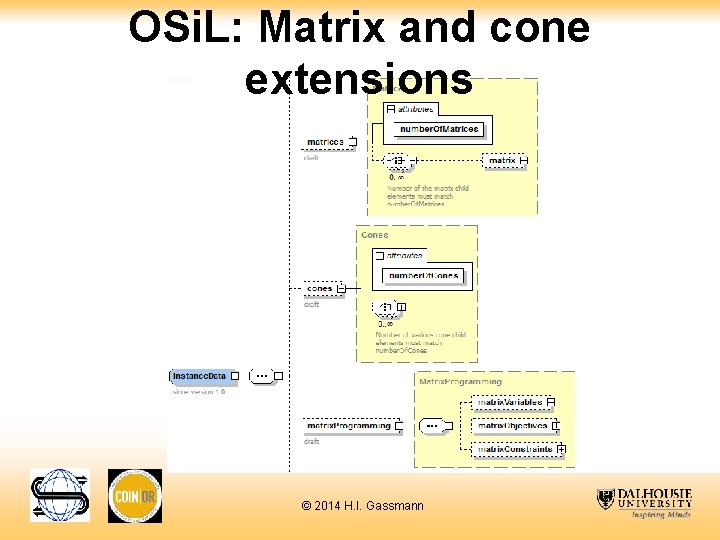
OSi. L: Matrix and cone extensions © 2014 H. I. Gassmann

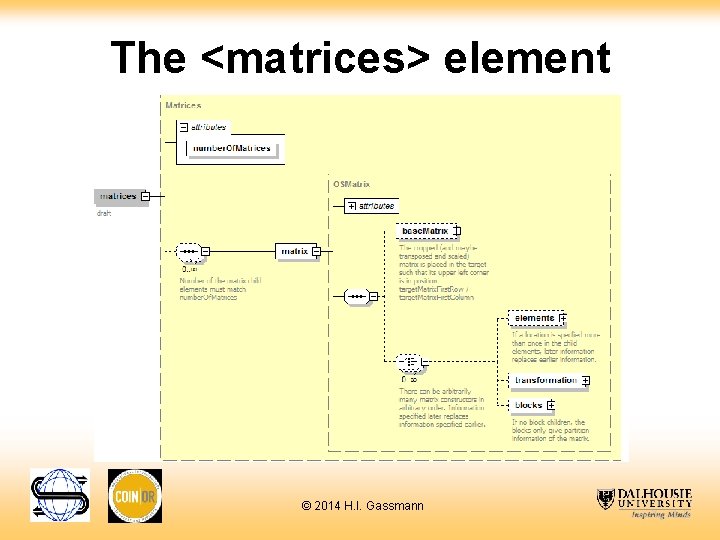
The <matrices> element © 2014 H. I. Gassmann

Example 1 – elements <matrices number. Of. Matrices= "4"> <matrix number. Of. Rows="2" number. Of. Columns="1"> <elements> <constant. Elements number. Of. El="2"> <start> <el> 0 </el> <el> 2 </el> </start> <indexes> <el> 0 </el> <el> 1 </el> </indexes> <values> <el> 1 </el> <el> 2 </el> </values> </constant. Elements> </elements > </matrix> © 2014 H. I. Gassmann

Example 2 - transformation <matrix number. Of. Rows="2" number. Of. Columns="2"> <transformation> <matrix. Times> <matrix. Idx="0"/> <matrix. Transpose> <matrix. Idx="0"/> </matrix. Transpose> </matrix. Times> </transformation> </matrix> © 2014 H. I. Gassmann

Example 3 - blocks <matrix number. Of. Rows="3" number. Of. Columns="4"> <blocks number. Of. Blocks="2"> <col. Offsets number. Of. El="3"> <el>0</el> <el>2</el> <el>4</el> </col. Offsets> <row. Offsets number. Of. El="3"> <el>0</el> <el>2</el> <el>3</el> </row. Offsets> <block. Row. Idx="0" block. Col. Idx="0"> <base. Matrix. Idx="1"/> </block> <block. Row. Idx="1" block. Col. Idx="1"> <base. Matrix. Idx="0" base. Transpose="true" scalar. Multiplier="-3"/> </blocks> </matrix> © 2014 H. I. Gassmann

Example 4 – base matrix <matrix number. Of. Rows="5" number. Of. Columns="5"> <base. Matrix. Idx="2" base. Matrix. First. Row="0" base. Matrix. First. Col="0" base. Matrix. Last. Row="2" base. Matrix. Last. Col="2" base. Transpose="false" scalar. Multiplier="1. 0" target. Matrix. First. Row="1" target. Matrix. Last. Row ="1" /> </matrix> © 2014 H. I. Gassmann

Example 5 – variable references <matrix number. Of. Rows="2" number. Of. Columns="2" symmetry="lower"> <elements> <var. Reference. Elements number. Of. El="3"> <start> <el> 0 </el> <el> 2 </el> <el> 3 </el> </start> <indexes> <el> 0 </el> <el> 1 </el> </indexes> <values> <el mult="3" incr="1"> 0 </el> </values> </var. Reference. Elements > </elements > </matrix> © 2014 H. I. Gassmann

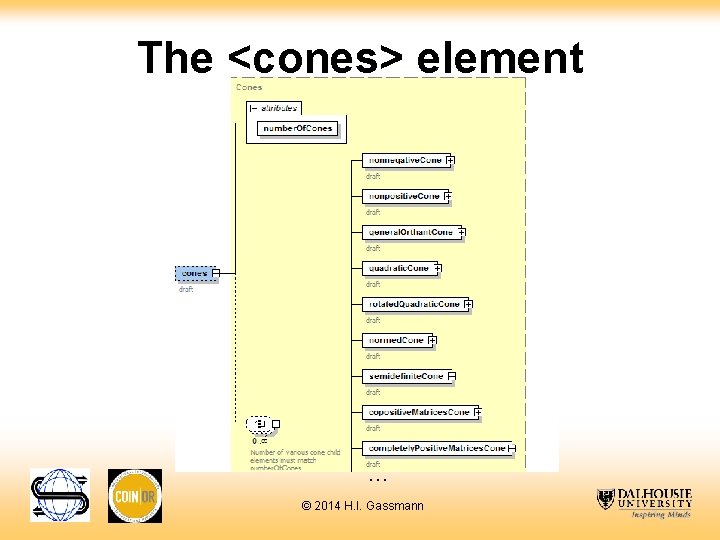
The <cones> element … © 2014 H. I. Gassmann

The <cones> element Example <cones number. Of. Cones="4"> <nonnegative. Cone number. Of. Rows= "2" number. Of. Columns= “ 2"/> <quadratic. Cone number. Of. Rows= "4" number. Of. Columns= "1"/> <semidefinite. Cone number. Of. Rows= "2" number. Of. Columns= "2"/> Cone of nonneg. poly. <nonnegative. Polynomials. Cone max. Degree="4" in two variables number. Of. Rows= "2" number. Of. Columns= "1"/> <intersection. Cone number. Of. Rows= "2" number. Of. Columns= “ 2"> <components number. Of. El="2“> Cone of symmetric positive <el>2</el> <el>0</el> semidefinite 2 x 2 matrices </components> with nonnegative entries </intersection. Cone> </cones> © 2014 H. I. Gassmann

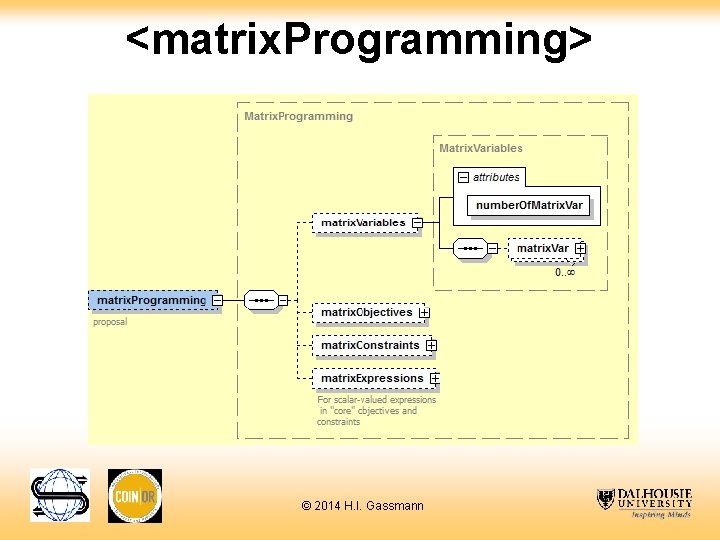
<matrix. Programming> © 2014 H. I. Gassmann

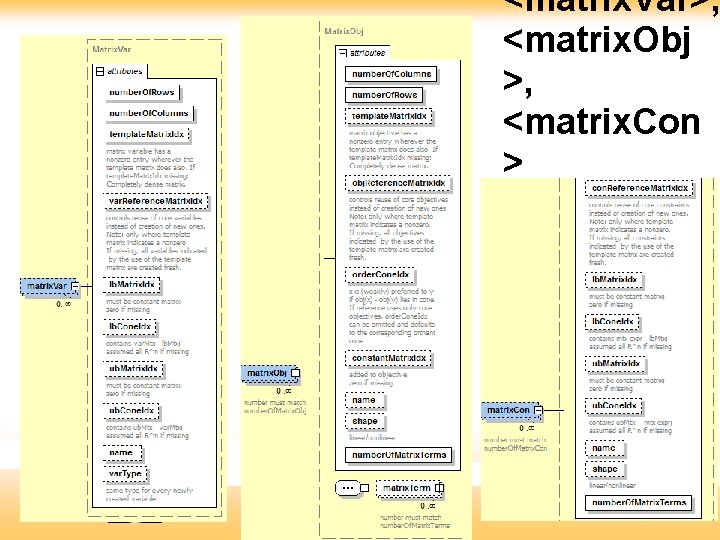
<matrix. Var>, <matrix. Obj >, <matrix. Con > © 2014 H. I. Gassmann

<matrix. Var> example Recall: C 0 is the cone of 2 x 2 positive semidefinite matrices X = M 4 is positive semidefinite (i. e. , in C 0): <matrix. Var number. Of. Rows="2" number. Of. Columns="2" var. Reference. Matrix. Idx="4" lb. Cone. Idx="0"/> © 2014 H. I. Gassmann

<matrix. Programming> example <matrix. Programming> <matrix. Variables number. Of. Matrix. Var="1"> <matrix. Var number. Of. Rows="2" number. Of. Columns="2" var. Reference. Matrix. Idx="4" lb. Cone. Idx="0"/> </matrix. Variables> <matrix. Expressions number. Of. Expr="3"> <expr idx="-1" shape="linear"> <matrix. Trace> <matrix. Times> <matrix. Idx="1"/> <matrix. Idx="4"/> </matrix. Times> </matrix. Trace> </expr> … </matrix. Expressions > </matrix. Programming> © 2014 H. I. Gassmann

Future work • Complete the parser • Translate SDP problems (SDPlib) • Write CSDP driver © 2014 H. I. Gassmann

How to get OS • Download – Binaries • http: //www. coin-or. org/download/binary/OS – OS-2. 1. 1 -win 32 -msvc 9. zip – OS-2. 3. 0 -linux-x 86_64 -gcc 4. 3. 2. tgz – Stable source • http: //www. coin-or. org/download/source/OS/ – OS-2. 8. 0. tgz – OS-2. 8. 0. zip – Development version (using svn) • svn co https: //projects. coin-or. org/svn/OS/releases/2. 8. 0 COIN-OS • svn co https: //projects. coin-or. org/svn/OS/trunk COIN© 2014 H. I. Gassmann OS

QUESTIONS? http: //www. optimizationservices. org https: //projects. coin-or. org/OS Horand. Gassmann@dal. ca © 2014 H. I. Gassmann