Extensional viscosity measurements of dragreducing polymer solutions using

Extensional viscosity measurements of dragreducing polymer solutions using a Capillary Break-up Extensional Rheometer Robert J Poole , Adam Swift and Marcel P Escudier Department of Engineering, University of Liverpool, UK ESR 2 nd Annual European Rheology Conference, April 21 -23, Grenoble-France

Outline • Introduction: Drag reduction and extensional viscosity • Fluid shear and oscillatory shear rheology • Capillary Break-up technique • Extensional viscosity data • Conclusions

Introductio n • (Turbulent) drag reduction by polymer additives first discovered by Toms (1948) (or Mysels (1949)). • Small additions (as little as a few p. p. m) of a polymer additive to a Newtonian solvent can reduce friction factor by up to 80%. Major reviews by • Lumley (1969) [185 cites] • Virk (1975) [310 cites] • Nieuwstadt and den Toonder (2001)* Still significant interest (>50 papers in 2004 and 15 papers already in 2005). *Turbulence structure and Modulation, (ed. A. Soldati and R. Monti) Springer

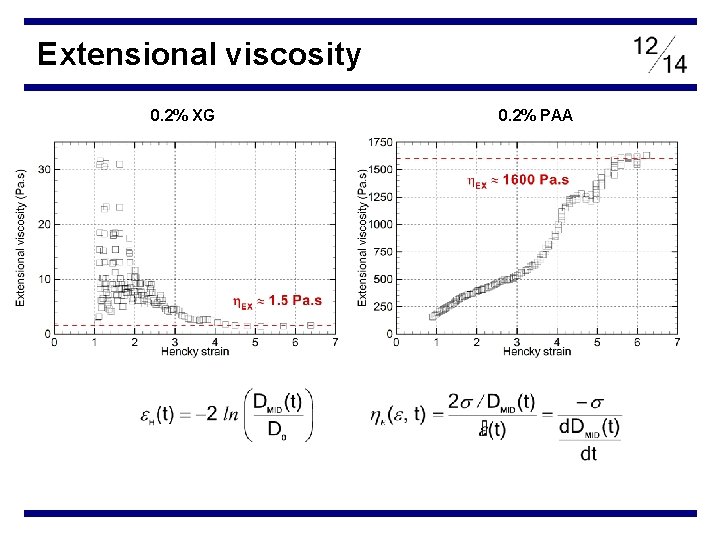
Introductio n 0. 4% CMC 0. 2% XG 0. 09% XG / 0. 09% CMC 0. 2% PAA A keyword in most attempts to explain the mechanism of drag reduction is extensional (or elongational) viscosity *Escudier, Presti and Smith (1999) Jn. NFM

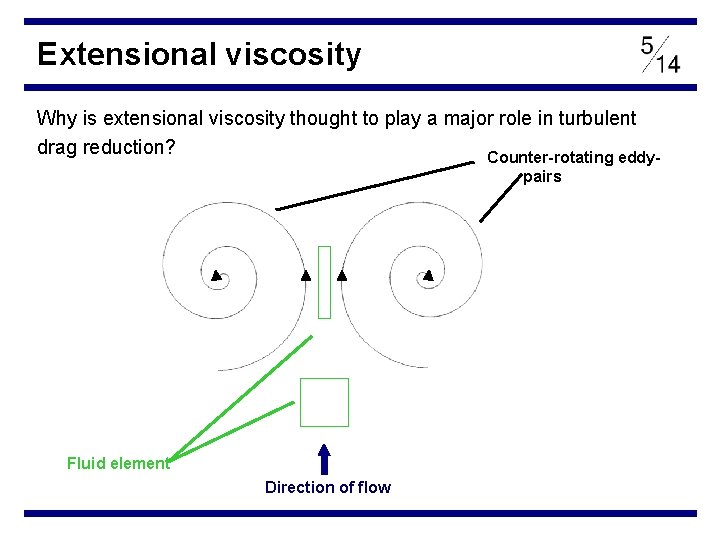
Extensional viscosity Why is extensional viscosity thought to play a major role in turbulent drag reduction? Counter-rotating eddypairs Fluid element Direction of flow

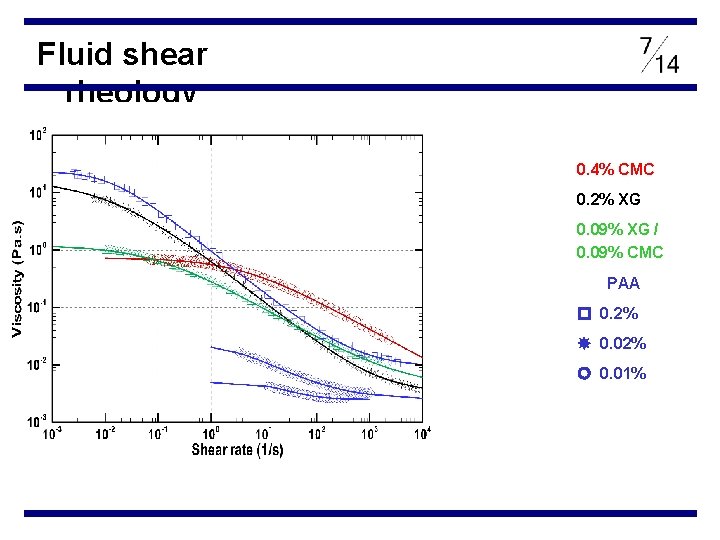
Fluid shear rheology Polymers studied (water as solvent for all): (a) Polyacrylamide (PAA 0. 2%, 0. 02% and 0. 01%) [Separan AP 273 E from Floreger] ‘Very flexible’ polymer, high molecular weight (2 x 106 g/mol) (b) 0. 2% Xanthan gum (XG) [Keltrol TF from Kelco]. Semi-rigid polymer, high molecular weight (5 x 106 g/mol) (c) 0. 4% Sodium carboxymethylcellulose (CMC) [Aldrich Grade 9004 -324] molecular weight (7 x 105 g/mol) (d) 0. 09% XG / 0. 09% CMC blend [same grades as unblended polymers]. (e)

Fluid shear rheology 0. 4% CMC 0. 2% XG 0. 09% XG / 0. 09% CMC PAA 0. 2% 0. 01%

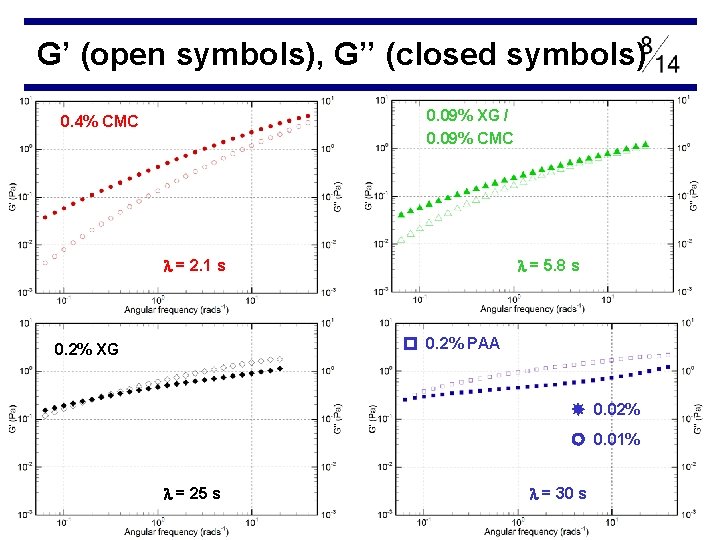
G’ (open symbols), G’’ (closed symbols) 0. 09% XG / 0. 09% CMC 0. 4% CMC = 2. 1 s = 5. 8 s 0. 2% PAA 0. 2% XG 0. 02% 0. 01% = 25 s = 30 s

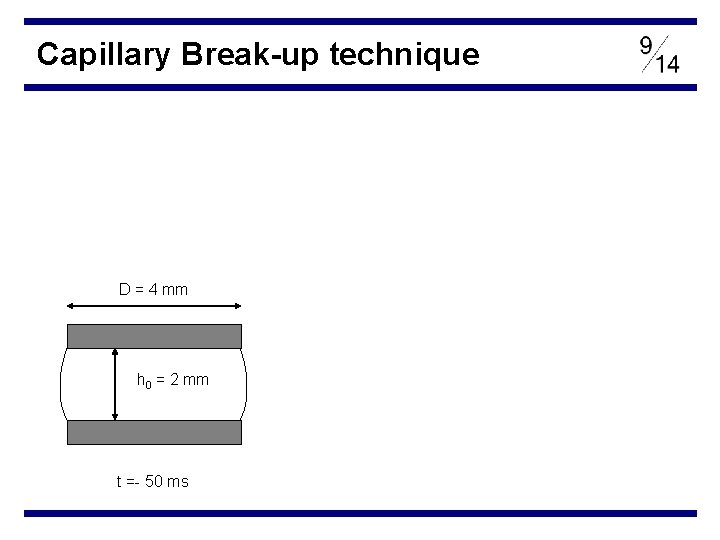
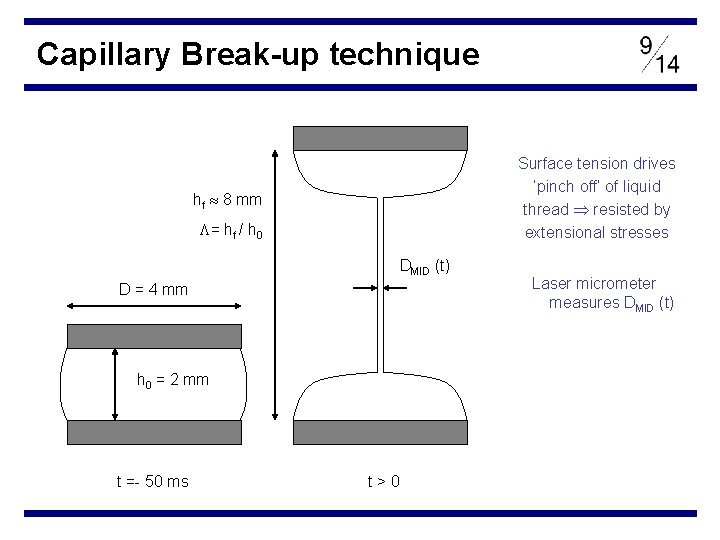
Capillary Break-up technique D = 4 mm h 0 = 2 mm t =- 50 ms

Capillary Break-up technique Surface tension drives ‘pinch off’ of liquid thread resisted by extensional stresses hf 8 mm = hf / h 0 DMID (t) D = 4 mm h 0 = 2 mm t =- 50 ms t>0 Laser micrometer measures DMID (t)

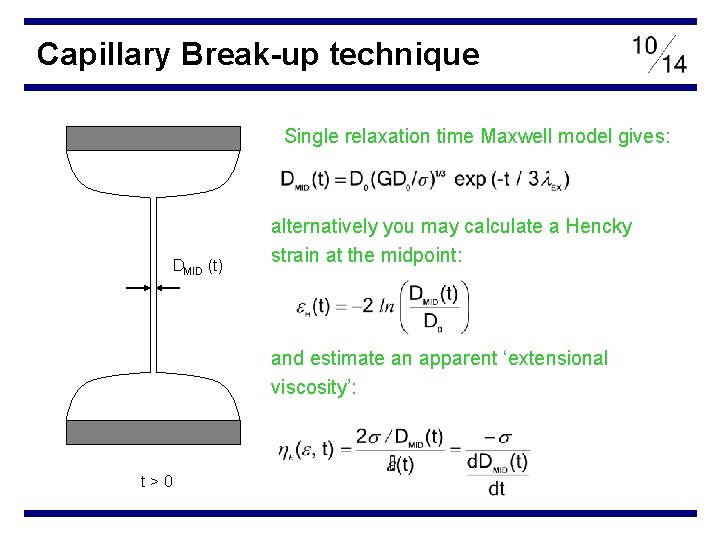
Capillary Break-up technique Single relaxation time Maxwell model gives: DMID (t) alternatively you may calculate a Hencky strain at the midpoint: and estimate an apparent ‘extensional viscosity’: t>0

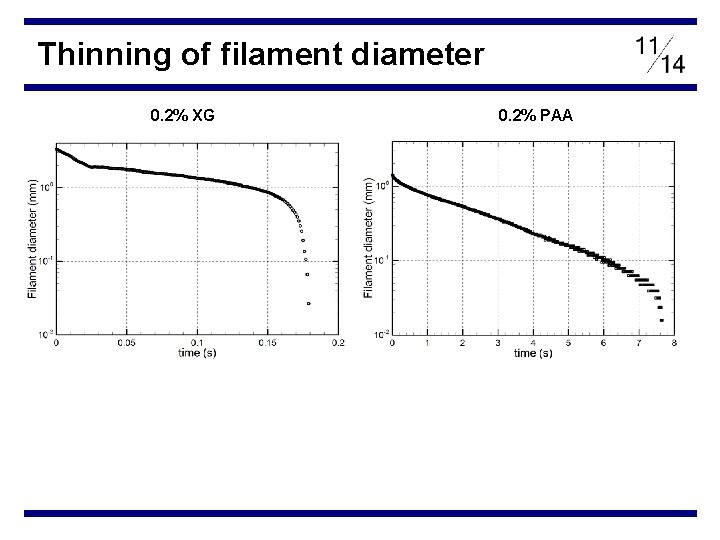
Thinning of filament diameter 0. 2% XG 0. 2% PAA

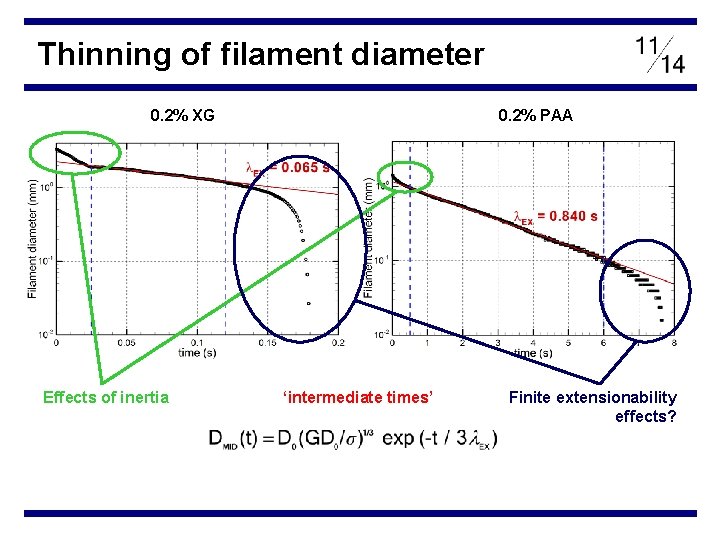
Thinning of filament diameter 0. 2% XG Effects of inertia 0. 2% PAA ‘intermediate times’ Finite extensionability effects?

Extensional viscosity 0. 2% XG 0. 2% PAA

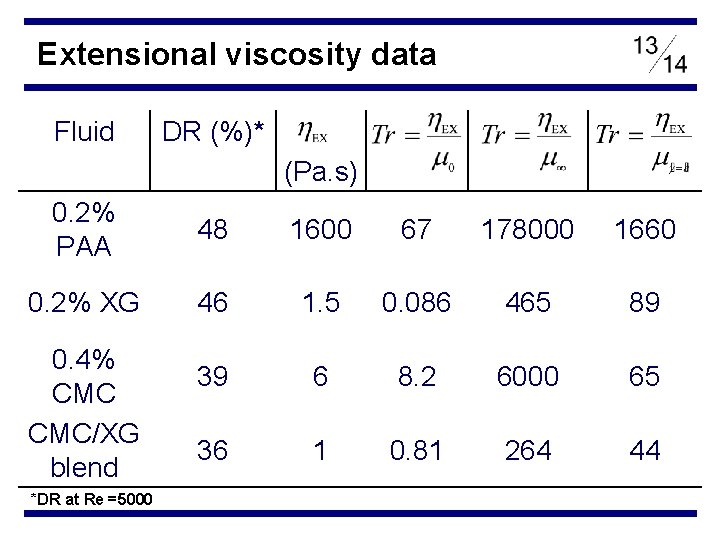
Extensional viscosity data Fluid DR (%)* (Pa. s) 0. 2% PAA 48 1600 67 178000 1660 0. 2% XG 46 1. 5 0. 086 465 89 39 6 8. 2 6000 65 36 1 0. 81 264 44 0. 4% CMC/XG blend *DR at Re =5000

Conclusions… • Capillary-thinning behaviour of PAA significantly different to XG, CMC and a XG/CMC blend • Extensional viscosity of PAA two orders of magnitude greater than XG (despite very similar levels of DR) • Biaxial not uniaxial extensional flows which are created by streamwise vortical structures? (Shaqfeh et al (2004) ICR)