EXTENSION OF LATIN HYPERCUBE SAMPLES WITH CORRELATED VARIABLES

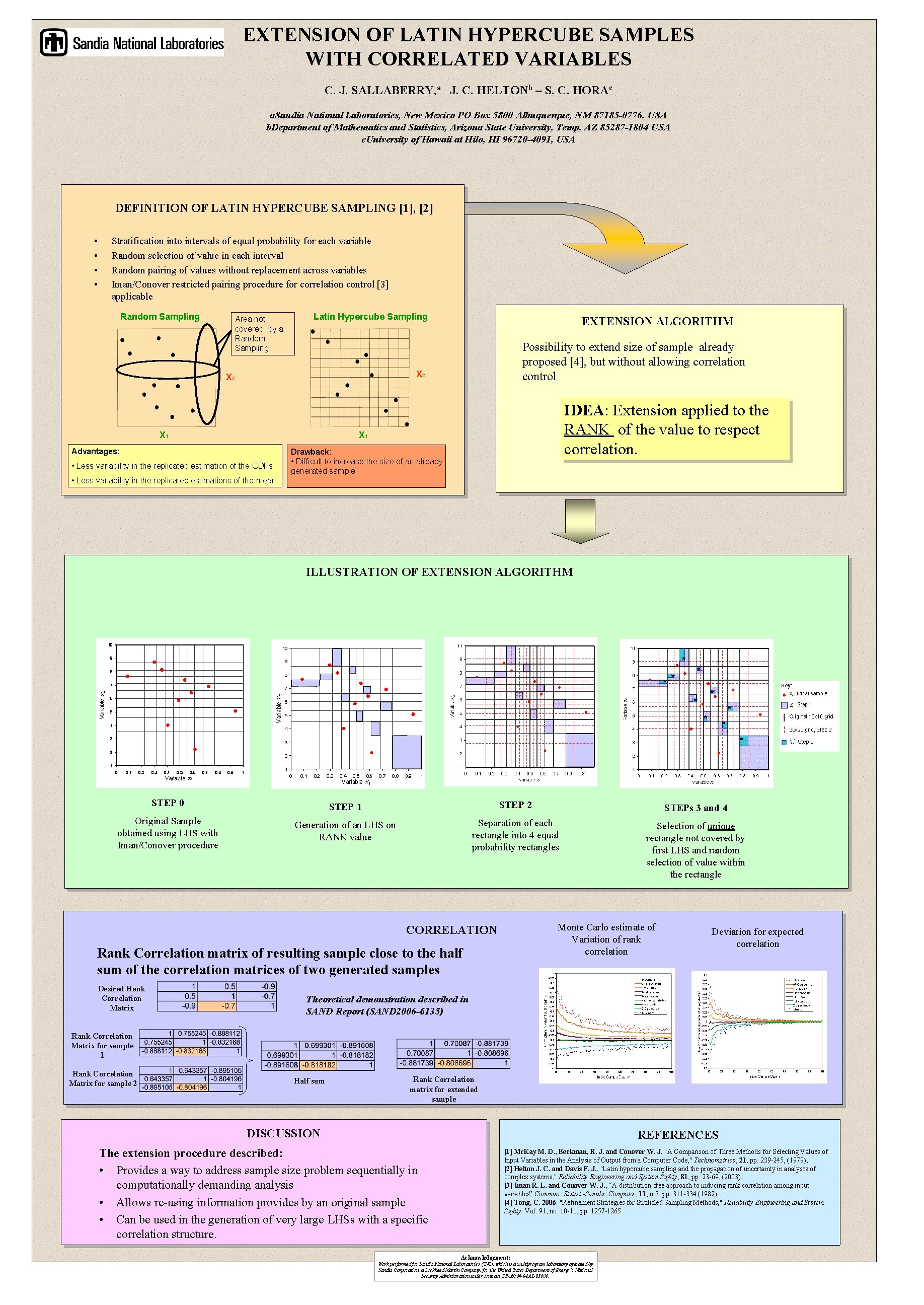
EXTENSION OF LATIN HYPERCUBE SAMPLES WITH CORRELATED VARIABLES C. J. SALLABERRY, a J. C. HELTONb – S. C. HORAc a. Sandia National Laboratories, New Mexico PO Box 5800 Albuquerque, NM 87185 -0776, USA b. Department of Mathematics and Statistics, Arizona State University, Temp, AZ 85287 -1804 USA c. University of Hawaii at Hilo, HI 96720 -4091, USA DEFINITION OF LATIN HYPERCUBE SAMPLING [1], [2] • • Stratification into intervals of equal probability for each variable Random selection of value in each interval Random pairing of values without replacement across variables Iman/Conover restricted pairing procedure for correlation control [3] applicable Random Sampling Area not covered by a Random Sampling Latin Hypercube Sampling EXTENSION ALGORITHM Possibility to extend size of sample already proposed [4], but without allowing correlation control X 2 X 1 IDEA: Extension applied to the RANK of the value to respect correlation. X 1 Advantages: • Less variability in the replicated estimation of the CDFs Drawback: • Difficult to increase the size of an already generated sample • Less variability in the replicated estimations of the mean ILLUSTRATION OF EXTENSION ALGORITHM STEP 0 STEP 1 STEP 2 STEPs 3 and 4 Original Sample obtained using LHS with Iman/Conover procedure Generation of an LHS on RANK value Separation of each rectangle into 4 equal probability rectangles Selection of unique rectangle not covered by first LHS and random selection of value within the rectangle Monte Carlo estimate of Variation of rank correlation CORRELATION Rank Correlation matrix of resulting sample close to the half sum of the correlation matrices of two generated samples Desired Rank Correlation Matrix Deviation for expected correlation Theoretical demonstration described in SAND Report (SAND 2006 -6135) Rank Correlation Matrix for sample 1 Rank Correlation Matrix for sample 2 Half sum Rank Correlation matrix for extended sample DISCUSSION REFERENCES The extension procedure described: • Provides a way to address sample size problem sequentially in computationally demanding analysis • Allows re-using information provides by an original sample • Can be used in the generation of very large LHSs with a specific correlation structure. [1] Mc. Kay M. D. , Beckman, R. J. and Conover W. J. "A Comparison of Three Methods for Selecting Values of Input Variables in the Analysis of Output from a Computer Code, " Technometrics, 21, pp. 239 -245, (1979), [2] Helton J. C. and Davis F. J. , "Latin hypercube sampling and the propagation of uncertainty in analyses of complex systems, " Reliability Engineering and System Safety, 81, pp. 23 -69, (2003), [3] Iman R. L. and Conover W. J. , “A distribution-free approach to inducing rank correlation among input variables” Commun. Statist. -Simula. Computa. , 11, n. 3, pp. 311 -334 (1982), [4] Tong, C. 2006. "Refinement Strategies for Stratified Sampling Methods, " Reliability Engineering and System Safety. Vol. 91, no. 10 -11, pp. 1257 -1265 Acknowledgement: Work performed for Sandia National Laboratories (SNL), which is a multiprogram laboratory operated by Sandia Corporation, a Lockheed Martin Company, for the United States Department of Energy’s National Security Administration under contract DE-AC 04 -94 AL-85000.