Extension and Evaluation of Multidimensional Scaling MDS for

Extension and Evaluation of Multidimensional Scaling (MDS) for Geometric Microphone Array Calibration Amarnag Subramanya and Stanley T. Birchfield Dept. of Electrical and Computer Engineering Clemson University Clemson, South Carolina USA

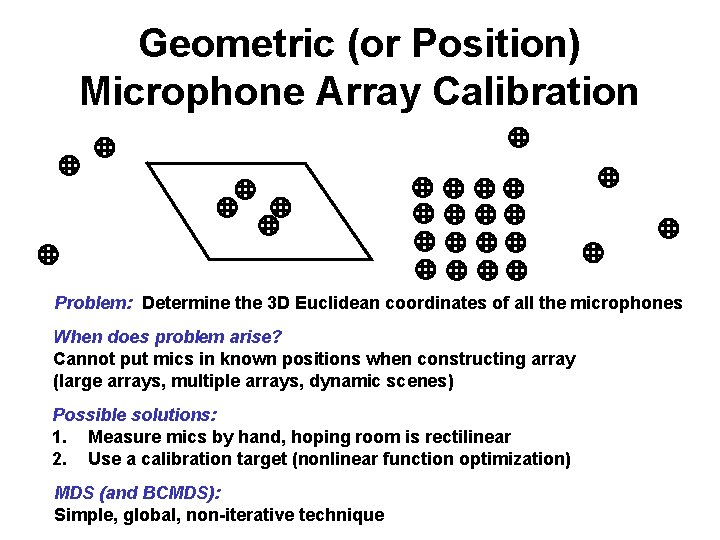
Geometric (or Position) Microphone Array Calibration Problem: Determine the 3 D Euclidean coordinates of all the microphones When does problem arise? Cannot put mics in known positions when constructing array (large arrays, multiple arrays, dynamic scenes) Possible solutions: 1. Measure mics by hand, hoping room is rectilinear 2. Use a calibration target (nonlinear function optimization) MDS (and BCMDS): Simple, global, non-iterative technique

Multidimensional scaling (MDS) MDS: Field of study for embedding points in low-dimensional space using their interpoint distances (psychology, biology, etc. ) Metric MDS: Distances are metric (Euclidean) Classical MDS: Specific technique for solving metric MDS problem [Young & Householder 1938, Torgerson 1952] SF LA NY DC 0 381 2944 2838 LA 381 0 2824 2685 NY 2944 2824 0 237 DC 2838 2685 237 0 SF

Classical MDS algorithm (same as PCA) To compute coordinates of n microphones in p-dimensional space from their pairwise distances: 1. Construct nxn squared-distance matrix D 2. Compute inner product matrix B = -1/2 JDJ, where is double-centering matrix 3. Decompose B as 4. Extract first p eigenvalues and eigenvectors 5. Coordinates are now in n x p matrix Matlab code: n = size(D, 1); J = eye(n) - ones( n)/n; B = -(1/2) * J*D*J; [u, s, v] = svd(B); rows = 1: ndim; Xout = u(: , rows)*s(rows, rows)^(1/2);

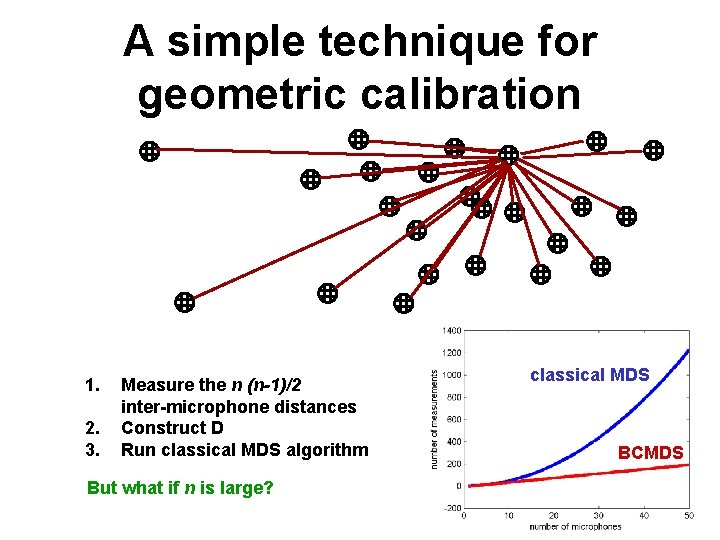
A simple technique for geometric calibration 1. 2. 3. Measure the n (n-1)/2 inter-microphone distances Construct D Run classical MDS algorithm But what if n is large? classical MDS BCMDS

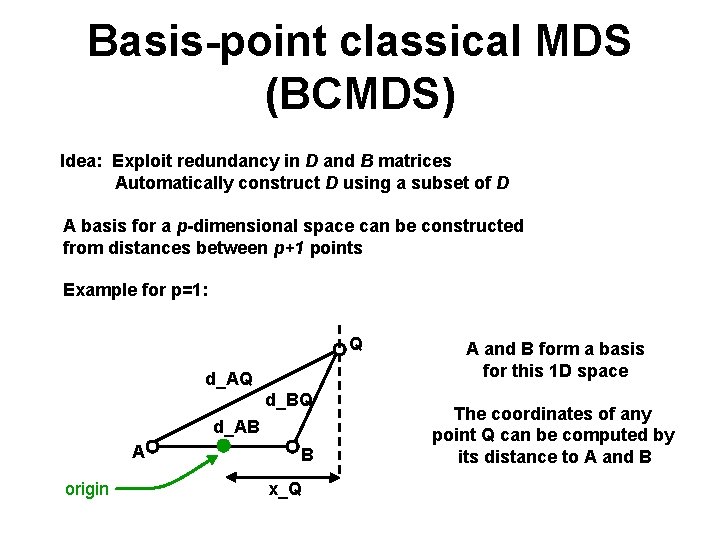
Basis-point classical MDS (BCMDS) Idea: Exploit redundancy in D and B matrices Automatically construct D using a subset of D A basis for a p-dimensional space can be constructed from distances between p+1 points Example for p=1: Q d_AQ d_BQ d_AB A origin B x_Q A and B form a basis for this 1 D space The coordinates of any point Q can be computed by its distance to A and B

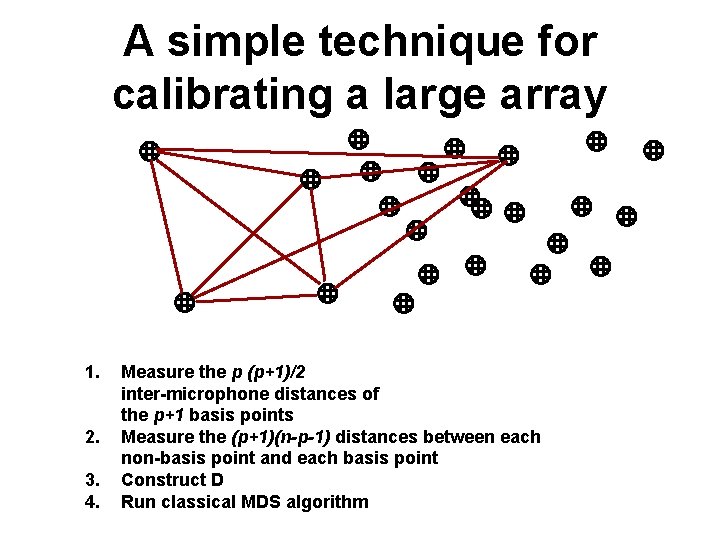
A simple technique for calibrating a large array 1. 2. 3. 4. Measure the p (p+1)/2 inter-microphone distances of the p+1 basis points Measure the (p+1)(n-p-1) distances between each non-basis point and each basis point Construct D Run classical MDS algorithm

Evaluation and sensitivity analysis

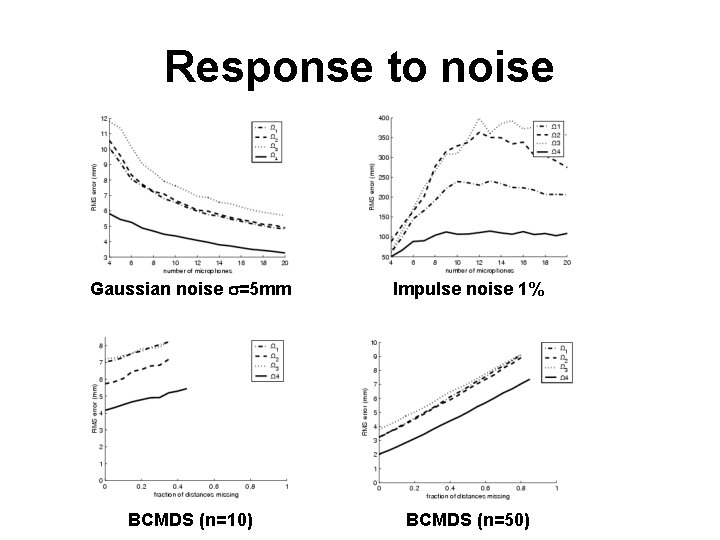
Response to noise Gaussian noise s=5 mm Impulse noise 1% BCMDS (n=10) BCMDS (n=50)

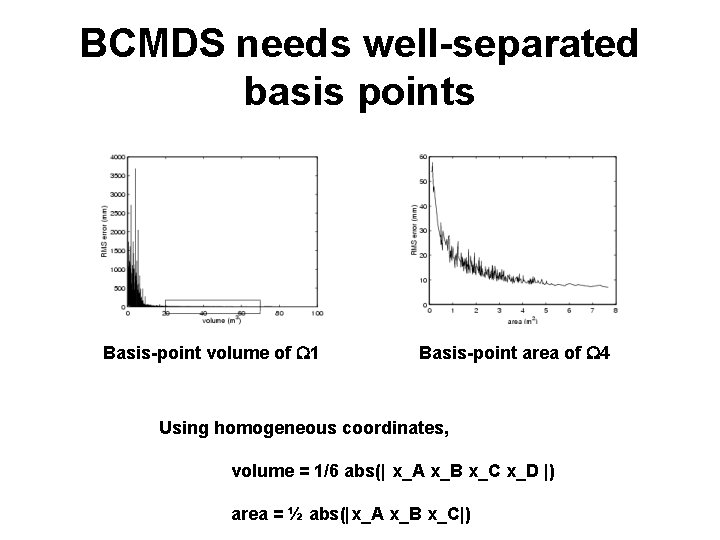
BCMDS needs well-separated basis points Basis-point volume of W 1 Basis-point area of W 4 Using homogeneous coordinates, volume = 1/6 abs(| x_A x_B x_C x_D |) area = ½ abs(|x_A x_B x_C|)

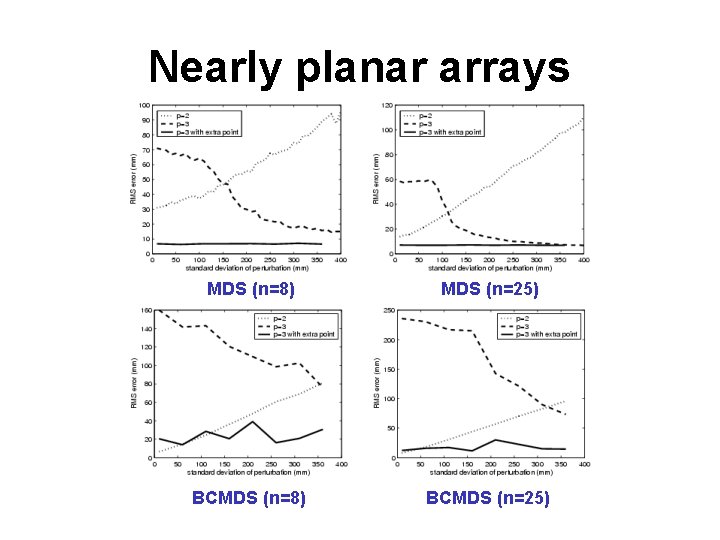
Nearly planar arrays MDS (n=8) MDS (n=25) BCMDS (n=8) BCMDS (n=25)

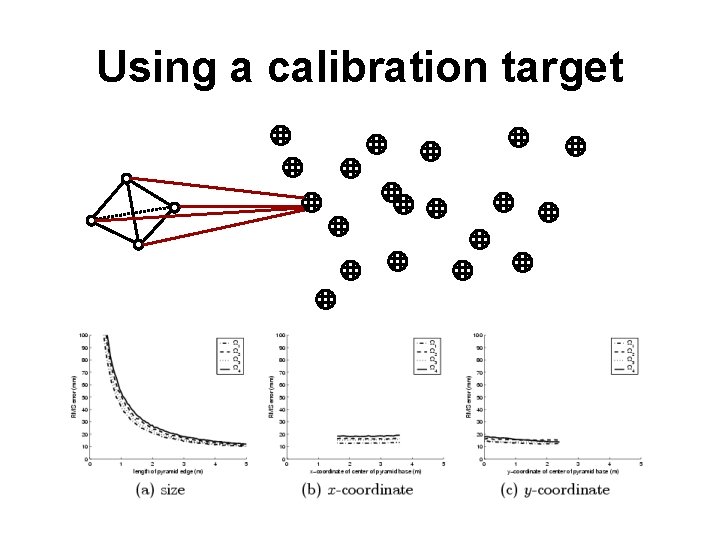
Using a calibration target

Conclusion Classical multidimensional scaling (classical MDS): Classical technique for computing coordinates of points from their interpoint distances Basis-point classical MDS (BCMDS): Extension requiring O(n) instead of O(n^2) distances These techniques 1. are simple, global, and non-iterative 2. automatically determine the angles of hand measurements 3. obviate the need for non-linear optimization 4. can be used with hand measurements or a calibration target 5. enable rapid recalibration for dynamic scenes 6. provide good initial estimate for nonlinear minimization