Extending the Link Transmission Model with general concave

Extending the Link Transmission Model with general concave fundamental diagrams and capacity drops Jeroen van der Gun Adam Pel Bart van Arem https: //beeldbank. rws. nl, Rijkswaterstaat / Joop van Houdt 1

Solving kinematic wave theory • Lighthill & Whitham (1955), Richards (1956) Formulation of kinematic wave theory • Godunov (1956), Daganzo (1994) Numerical solution through Cell Transmission Model • Newell (1993), Yperman et al. (2006), Yperman (2007), Gentile (2010) Alternative numerical solution through Link Transmission Model • Daganzo (2005), Jin (2015), Han et al. (2015) Proofs using variational theory that LTM converges for triangular fundamental diagrams as Δt↓ 0 2

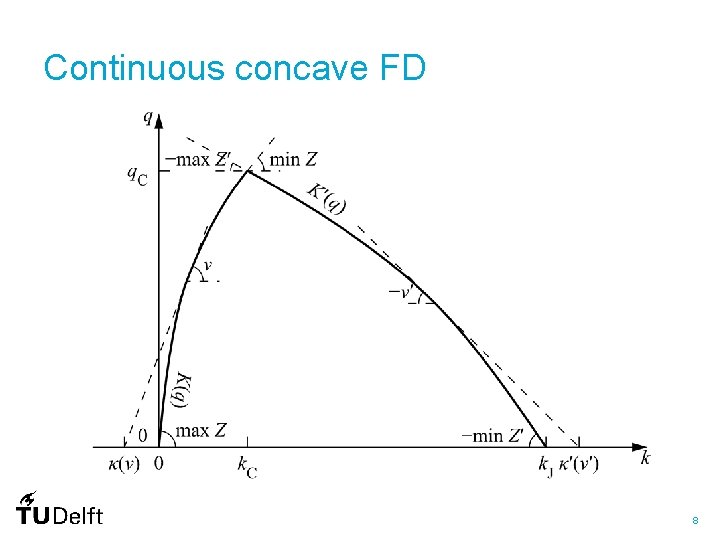
Triangular fundamental diagrams • Constant speed in subcritical traffic – Constant travel times in light traffic • Identical capacity in free-flow and congestion – No capacity drop – No benefit of metering https: //beeldbank. rws. nl, Rijkswaterstaat / DVK-RWS 3

Contents • Overview of LTM structure • Link model for continuous concave FD • LWR theory with capacity drop • Link model with capacity drop • Node model with capacity drop • Numerical examples 4

Overview of LTM structure 5

LTM structure (discrete time version) 6

Link model for continuous concave FD 7

Continuous concave FD 8

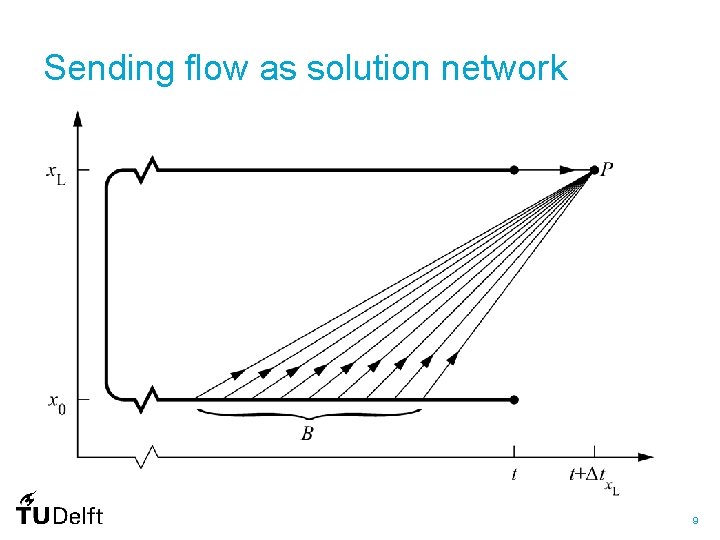
Sending flow as solution network 9

LWR theory with capacity drop 10

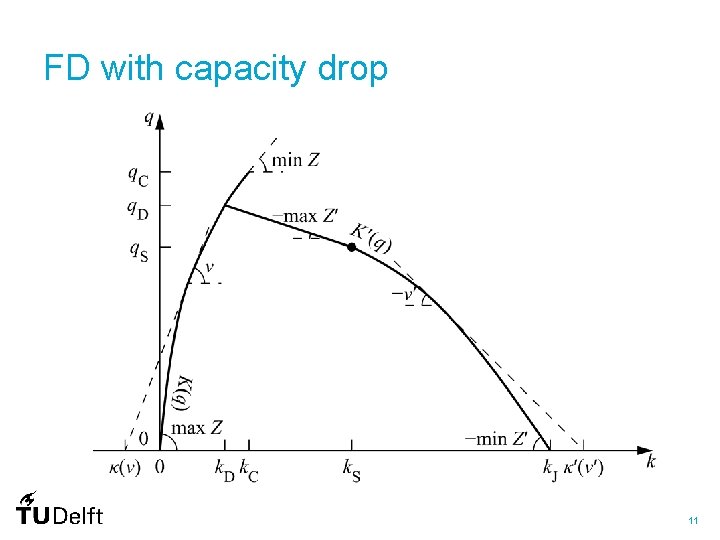
FD with capacity drop 11

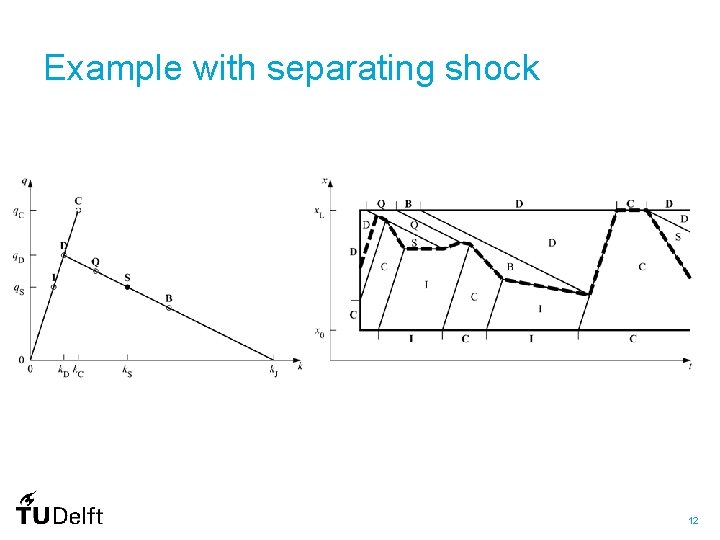
Example with separating shock 12

Link model with capacity drop 13

Link algorithm modifications • Sending flow – Add queue discharge rate constraint in congestion • Receiving flow – Apply backward paths only in case link outflow was congested – Track separating shock implicitly by adding extra paths • New dissolution procedure 14

Node model with capacity drop 15

Node algorithm modifications • Capacity drop invariance – First time step after breakdown same flow as later time steps • Standing queues with capacity drop – Congested transition flows never exceed discharge rate – Receiving flow reduced to discharge rate if exceeded – No memory effect 16

Numerical examples 17

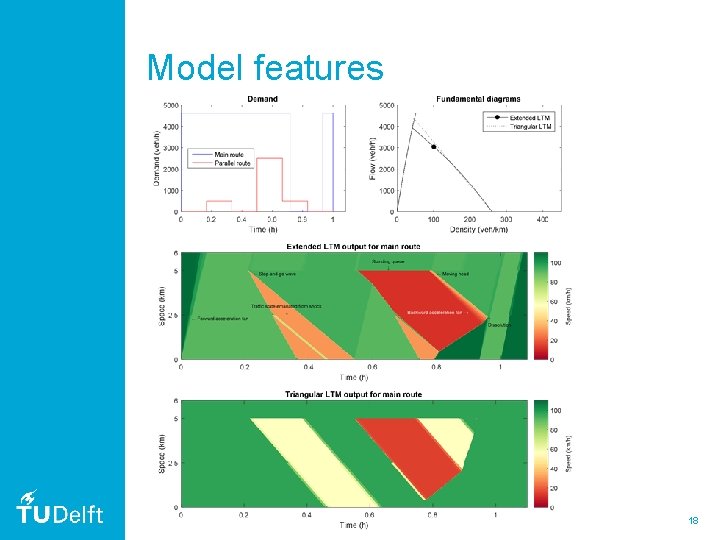
Model features 18

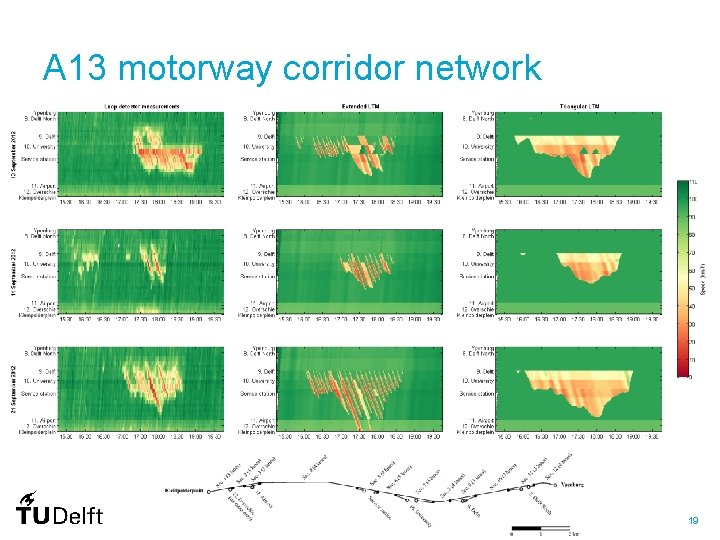
A 13 motorway corridor network 19

Conclusions 20

Conclusions • • LTM extended with continuous concave FDs LWR and LTM extended with capacity drop Models acceleration fans Models both onset and propagation of both standing and moving queues, including stopand-go waves • Computationally-efficient first-order network model with small numerical error J. P. T. vander. Gun@tudelft. nl 21