Extending Spatial Hot Spot Detection Techniques to Temporal

Extending Spatial Hot Spot Detection Techniques to Temporal Dimensions Sungsoon Hwang Department of Geography State University of New York at Buffalo DMGIS ’ 05

Outlines • Introduction – – • Approaches to hot spot detection Spatial statistical approach to hot spot detection (point pattern analysis) Review of point pattern analysis Time in point pattern analysis Extending K function to temporal dimensions – Space K function – Time K function – Space-time K function • Case studies: detecting traffic accident hot spots – Fatal motor vehicle crashes in New York State between ’ 96 – ‘ 01 – Fatal motor vehicle crashes in New York City between ’ 96 – ‘ 01 • Conclusions

Approaches to detecting hot spots • Non-spatial statistical approach – Designed to derive homogenous groupings – Not limited to 2 -D geographic space (i. e. multidimensional) – Space is not properly treated • Spatial statistical approach – Tests departures from complete spatial randomness – Takes into account the nature of spatial behavior – Also known as “point pattern analysis”

Review of point pattern analysis • Global statistics (intensity) – Quadrat method: # events in a given spatial frame – Kernel estimation: smoothing based on probability distribution • Local statistics (spatial dependence) – Nearest neighbor: detects the tendency for localized pattern at the smallest scales – K function: detects hot spots at varying scales

Time in point pattern analysis • Time provides important clues in spatial point pattern analysis – For understanding causality (e. g. before/after) – Intensity of spatial events varies by time • Previous studies – Knox’s test for space-time interaction (Knox 1964) – Temporal extension to K function (Diggle et al. 1995)

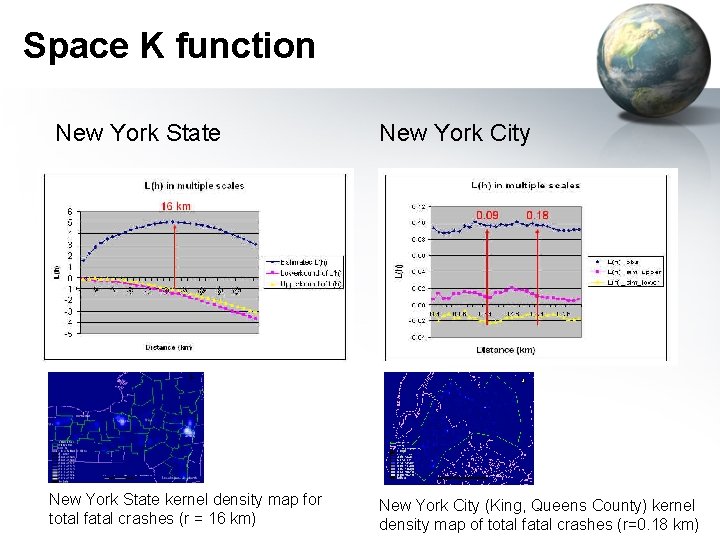
Space K function • K function • • • R is area of study area, n is the total number of observed events, h is the distance considered for local scale variation (or band size), dij is the distance between event i and event j, Ih is 1 if dij < h, or is 0 otherwise, wij is the adjustment factor of edge effect. • Test for spatial clustering • High positive value of L(h) indicates spatial clustering • Peak at L(h) across h indicates optimal scale

Time K function • K function • • Test for temporal clustering L: total duration n: total number of observed events t: time interval dij: interval between i and j I: 1 if dij < t , 0 otherwise wij: adjustment factor of edge effect

Space-time K function • Extension of space K function • Extension of time K function • Spatio-temporal K function

Study areas Motor Vehicle Crash, New York State ’ 96 – ‘ 01 Motor Vehicle Crash, New York City ’ 96 – ‘ 01 Source data: Fatality Analysis Reporting System (FARS), NHTSA

Space K function New York State kernel density map for total fatal crashes (r = 16 km) New York City (King, Queens County) kernel density map of total fatal crashes (r=0. 18 km)

Time K function New York State New York City

Extension of space K function New York State kernel density map for fatal crashes in May (r=30 km) New York City kernel density map of fatal crashes on November (r=0. 36)

Conclusions • Space K function detects spatial clusters • Time K function detects temporal clusters • Space-time K function detects – Temporal extension of space K function: detects spatial clusters of point events stratified by categorical temporal attributes – Spatial extension of temporal K function: detects temporal clusters of point events stratified by categorical spatial attributes – Spatio-temporal K function: detects space-time interaction • Case studies demonstrate that temporal extension of space K function is useful in discovering pattern that would have been unnoticed if observed events were not disaggregated by temporal types and if the whole range of possible scales were not explored.