Extendible Hashing For Use as a File Structure
Extendible Hashing For Use as a File Structure 1

External Hashing z. What if the hash table is a file in which each bucket is a record in that file? z. Observations: y. A bucket may contain more than one key value. y. The number of buckets may expand or contract dynamically. 2

Extendible Hashing z. Handling multiple key values per bucket is not a problem. z. Collisions are resolved with overflow buckets rather than the next bucket. z. Keep track of the number of times all buckets have been split (the “level”) and the next bucket to split. 3

The Hash Function z. The standard hash function would now be something like: H(x, L) = x mod (n * 2 L) z“L” is the level, initially zero. z. If H(x, L) < b, then calculate H(x, L+1). z“b” is the next bucket to split. 4

The “Split” z. Questions: y. When do I split the next bucket? y. What does a split entail? z. We split when the load factor exceeds a certain threshold. The load factor is the number of key values / number of slots. z. A split entails creating a new bucket and rehashing all keys in bucket b at level L+1. 5

The Insert Algorithm z. Initialize L = 0 and b = 0; z. Calculate bucket = H(x, L) yif (bucket < b) bucket = H(x, L+1) z. If bucket has an empty slot, fill it with x y. Else, create an overflow bucket for x z. If the new load factor >= the threshold y. Add new bucket at end y. Rehash all key values in bucket b at Level L+1 6 y. Add one to b.

The Insert Algorithm II z. If b = n * 2 L z. We have split all the buckets at the current level, so y. L = L + 1 yb = 0 7

Insert Example 0 1 2 b=0, L=0 H(x) = x mod 3*2 L 2 key values /bucket Load factor = 0/6 = 0 threshold = 0. 75 Insert: 24, 10, 15, 33, 60, 11, 61, 41 z. Insert 24: zbucket = H(24, 0) = 0 zbucket >= b, so bucket 0 it is: 8
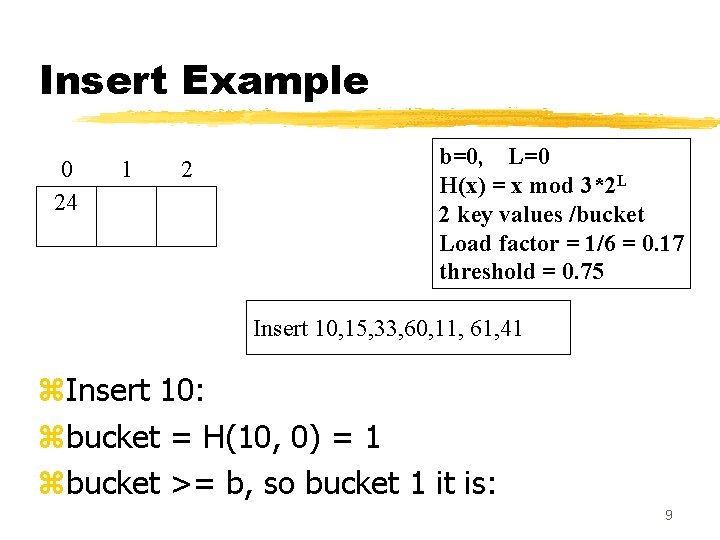
Insert Example 0 24 1 2 b=0, L=0 H(x) = x mod 3*2 L 2 key values /bucket Load factor = 1/6 = 0. 17 threshold = 0. 75 Insert 10, 15, 33, 60, 11, 61, 41 z. Insert 10: zbucket = H(10, 0) = 1 zbucket >= b, so bucket 1 it is: 9
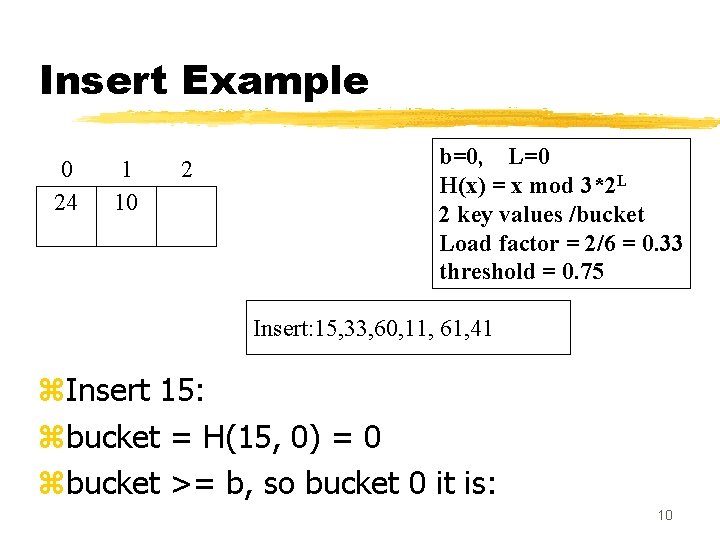
Insert Example 0 24 1 10 2 b=0, L=0 H(x) = x mod 3*2 L 2 key values /bucket Load factor = 2/6 = 0. 33 threshold = 0. 75 Insert: 15, 33, 60, 11, 61, 41 z. Insert 15: zbucket = H(15, 0) = 0 zbucket >= b, so bucket 0 it is: 10
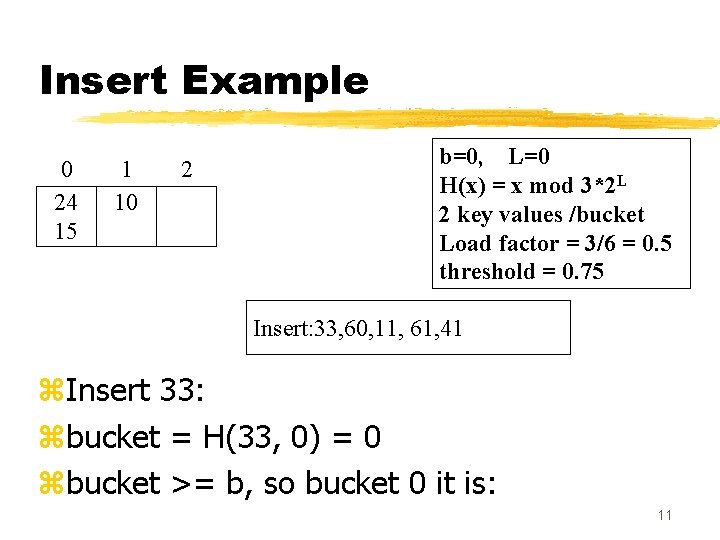
Insert Example 0 24 15 1 10 2 b=0, L=0 H(x) = x mod 3*2 L 2 key values /bucket Load factor = 3/6 = 0. 5 threshold = 0. 75 Insert: 33, 60, 11, 61, 41 z. Insert 33: zbucket = H(33, 0) = 0 zbucket >= b, so bucket 0 it is: 11

Insert Example 0 24 15 33 1 10 b=0, L=0 H(x) = x mod 3*2 L 2 key values /bucket Load factor = 4/6 = 0. 67 threshold = 0. 75 2 Insert: 60, 11, 61, 41 z. This requires an overflow bucket. z. Let’s assume overflow buckets also can hold 2 key values. z. Now, update load factor: 12
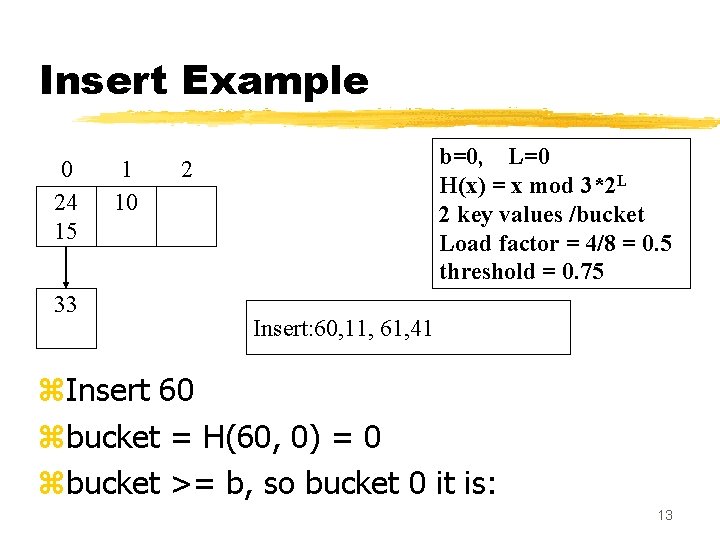
Insert Example 0 24 15 33 1 10 b=0, L=0 H(x) = x mod 3*2 L 2 key values /bucket Load factor = 4/8 = 0. 5 threshold = 0. 75 2 Insert: 60, 11, 61, 41 z. Insert 60 zbucket = H(60, 0) = 0 zbucket >= b, so bucket 0 it is: 13
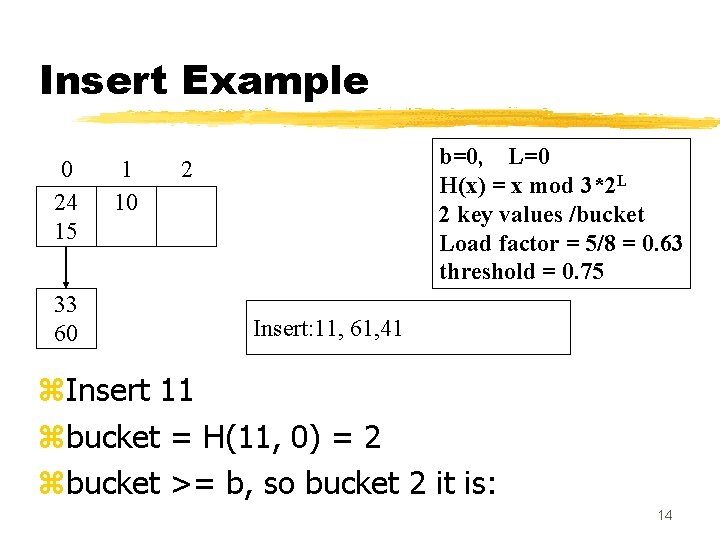
Insert Example 0 24 15 33 60 1 10 b=0, L=0 H(x) = x mod 3*2 L 2 key values /bucket Load factor = 5/8 = 0. 63 threshold = 0. 75 2 Insert: 11, 61, 41 z. Insert 11 zbucket = H(11, 0) = 2 zbucket >= b, so bucket 2 it is: 14
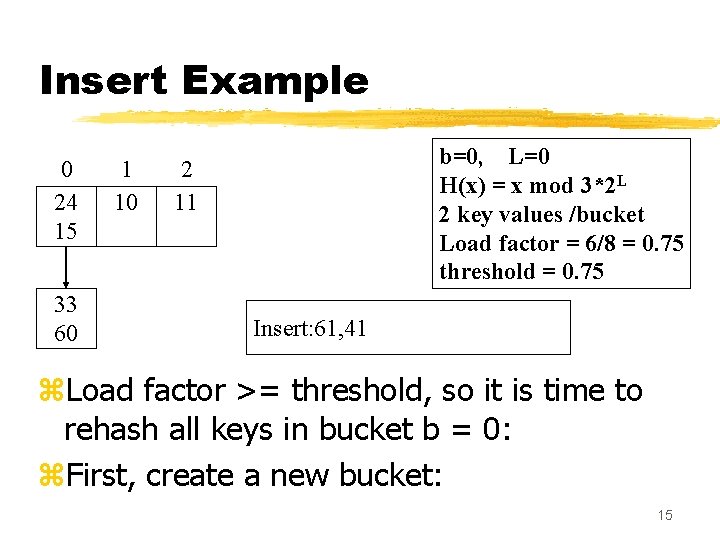
Insert Example 0 24 15 33 60 1 10 b=0, L=0 H(x) = x mod 3*2 L 2 key values /bucket Load factor = 6/8 = 0. 75 threshold = 0. 75 2 11 Insert: 61, 41 z. Load factor >= threshold, so it is time to rehash all keys in bucket b = 0: z. First, create a new bucket: 15
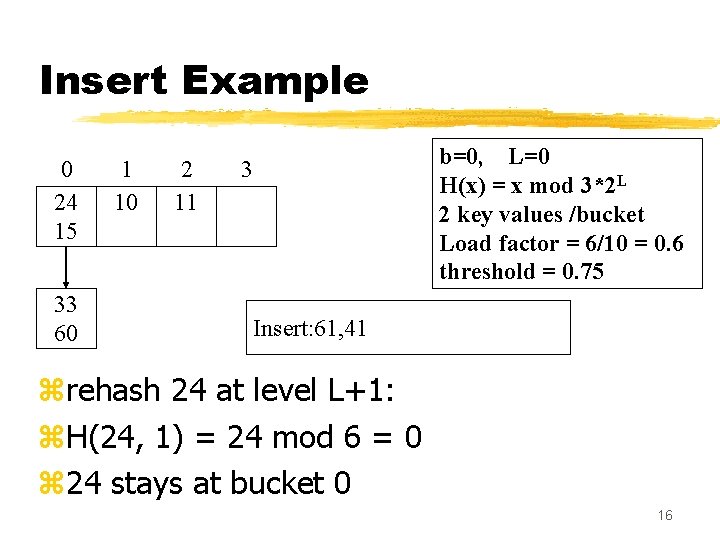
Insert Example 0 24 15 33 60 1 10 2 11 b=0, L=0 H(x) = x mod 3*2 L 2 key values /bucket Load factor = 6/10 = 0. 6 threshold = 0. 75 3 Insert: 61, 41 zrehash 24 at level L+1: z. H(24, 1) = 24 mod 6 = 0 z 24 stays at bucket 0 16
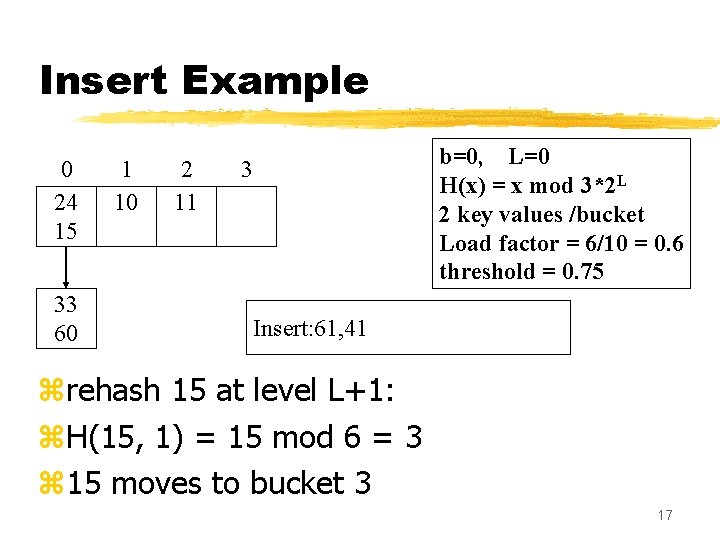
Insert Example 0 24 15 33 60 1 10 2 11 b=0, L=0 H(x) = x mod 3*2 L 2 key values /bucket Load factor = 6/10 = 0. 6 threshold = 0. 75 3 Insert: 61, 41 zrehash 15 at level L+1: z. H(15, 1) = 15 mod 6 = 3 z 15 moves to bucket 3 17
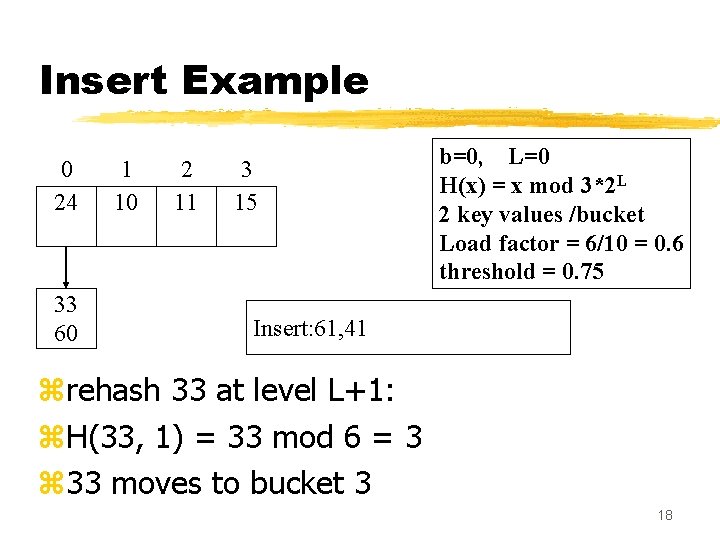
Insert Example 0 24 33 60 1 10 2 11 3 15 b=0, L=0 H(x) = x mod 3*2 L 2 key values /bucket Load factor = 6/10 = 0. 6 threshold = 0. 75 Insert: 61, 41 zrehash 33 at level L+1: z. H(33, 1) = 33 mod 6 = 3 z 33 moves to bucket 3 18
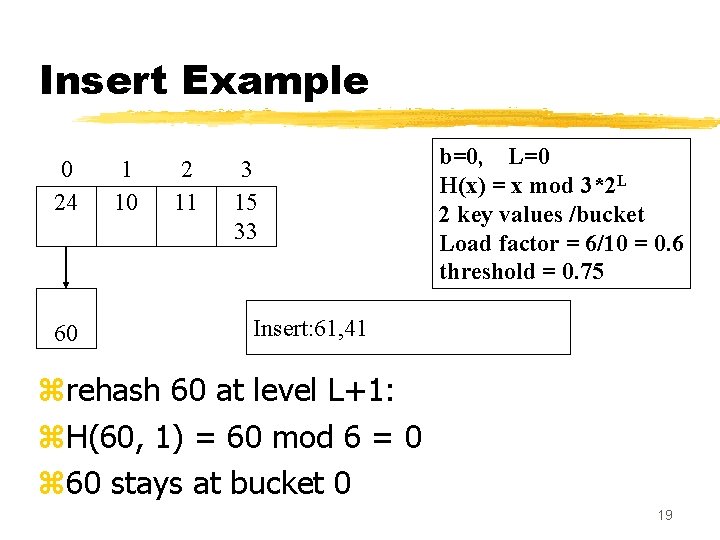
Insert Example 0 24 60 1 10 2 11 3 15 33 b=0, L=0 H(x) = x mod 3*2 L 2 key values /bucket Load factor = 6/10 = 0. 6 threshold = 0. 75 Insert: 61, 41 zrehash 60 at level L+1: z. H(60, 1) = 60 mod 6 = 0 z 60 stays at bucket 0 19

Insert Example 0 24 60 1 10 2 11 3 15 33 b=0, L=0 H(x) = x mod 3*2 L 2 key values /bucket Load factor = 6/10 = 0. 6 threshold = 0. 75 Insert: 61, 41 z. Add 1 to b; it is less than 3, so done with first split. z. I now have an empty overflow bucket; 20 remove it and recalculate load factor:
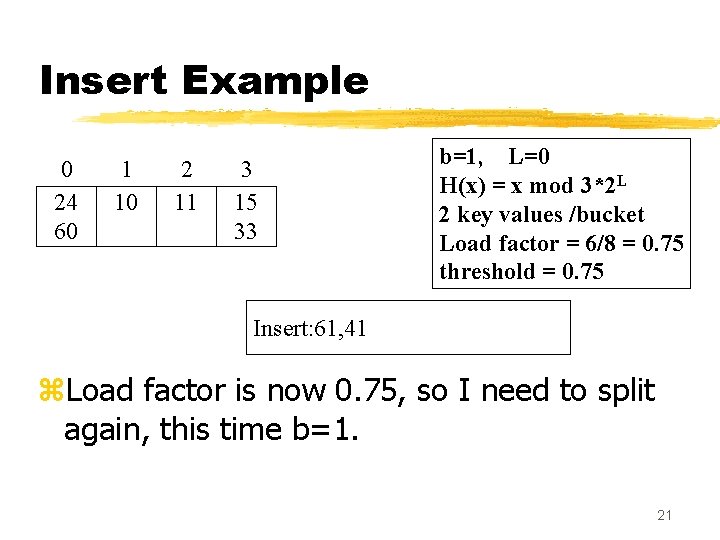
Insert Example 0 24 60 1 10 2 11 3 15 33 b=1, L=0 H(x) = x mod 3*2 L 2 key values /bucket Load factor = 6/8 = 0. 75 threshold = 0. 75 Insert: 61, 41 z. Load factor is now 0. 75, so I need to split again, this time b=1. 21
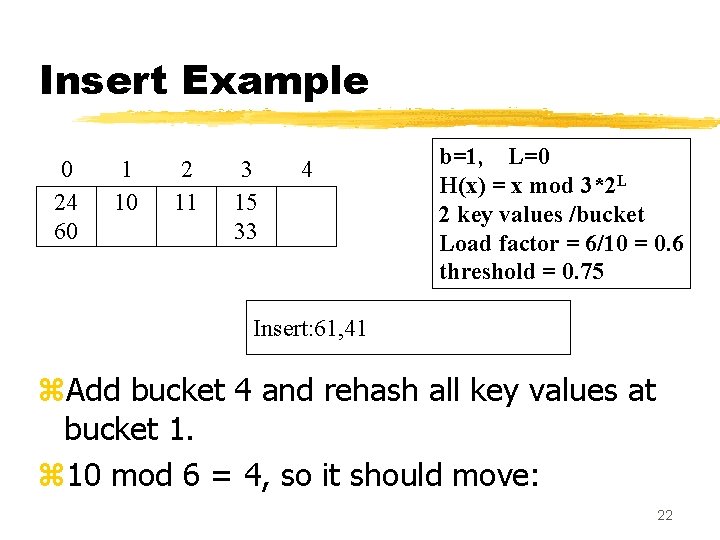
Insert Example 0 24 60 1 10 2 11 3 15 33 4 b=1, L=0 H(x) = x mod 3*2 L 2 key values /bucket Load factor = 6/10 = 0. 6 threshold = 0. 75 Insert: 61, 41 z. Add bucket 4 and rehash all key values at bucket 1. z 10 mod 6 = 4, so it should move: 22

Insert Example 0 24 60 1 2 11 3 15 33 4 10 b=2, L=0 H(x) = x mod 3*2 L 2 key values /bucket Load factor = 6/10 = 0. 6 threshold = 0. 75 Insert: 61, 41 z. Note update of b to 2; the load factor is OK, so continue with insert of 61. 23
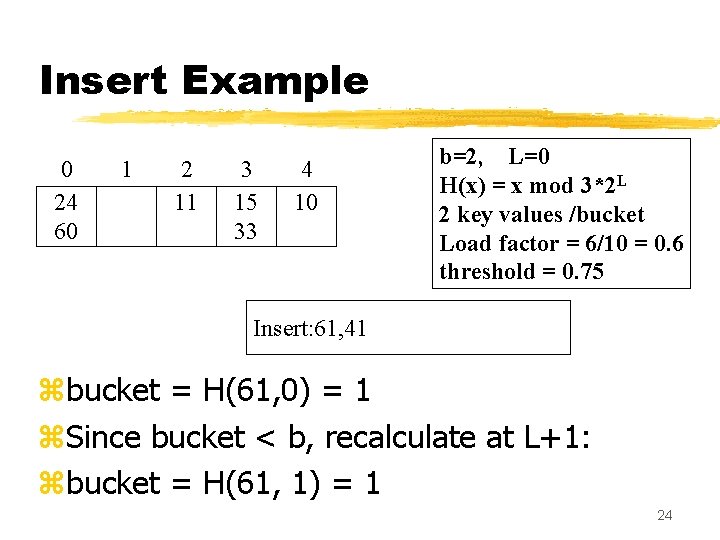
Insert Example 0 24 60 1 2 11 3 15 33 4 10 b=2, L=0 H(x) = x mod 3*2 L 2 key values /bucket Load factor = 6/10 = 0. 6 threshold = 0. 75 Insert: 61, 41 zbucket = H(61, 0) = 1 z. Since bucket < b, recalculate at L+1: zbucket = H(61, 1) = 1 24
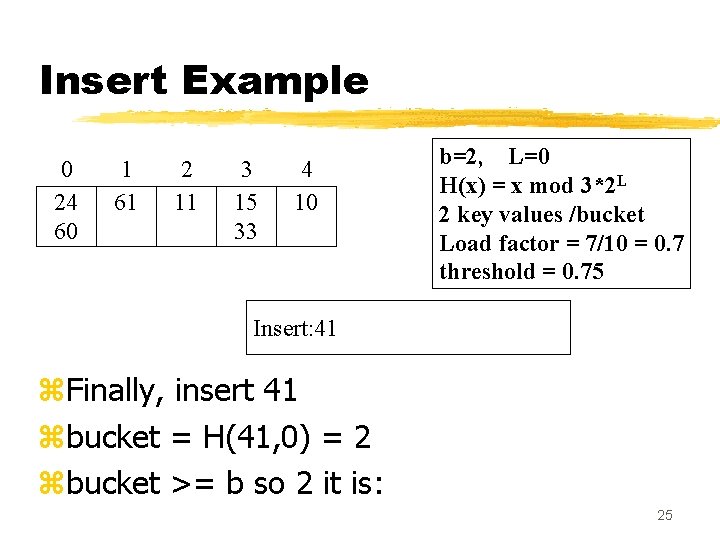
Insert Example 0 24 60 1 61 2 11 3 15 33 4 10 b=2, L=0 H(x) = x mod 3*2 L 2 key values /bucket Load factor = 7/10 = 0. 7 threshold = 0. 75 Insert: 41 z. Finally, insert 41 zbucket = H(41, 0) = 2 zbucket >= b so 2 it is: 25
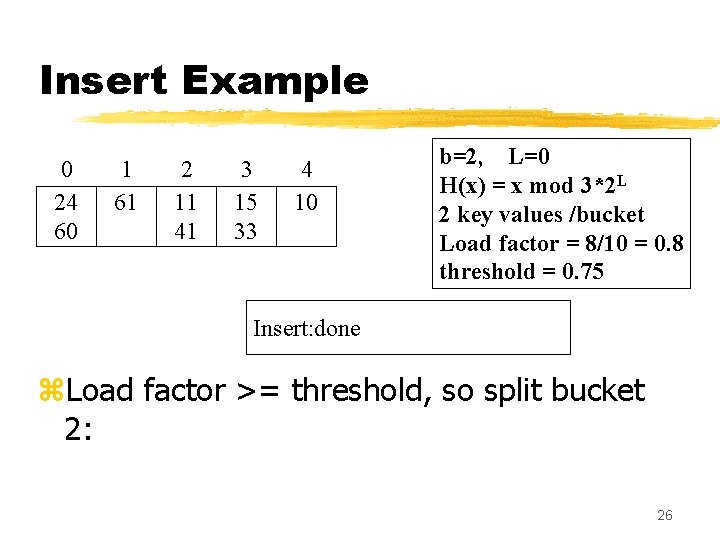
Insert Example 0 24 60 1 61 2 11 41 3 15 33 4 10 b=2, L=0 H(x) = x mod 3*2 L 2 key values /bucket Load factor = 8/10 = 0. 8 threshold = 0. 75 Insert: done z. Load factor >= threshold, so split bucket 2: 26
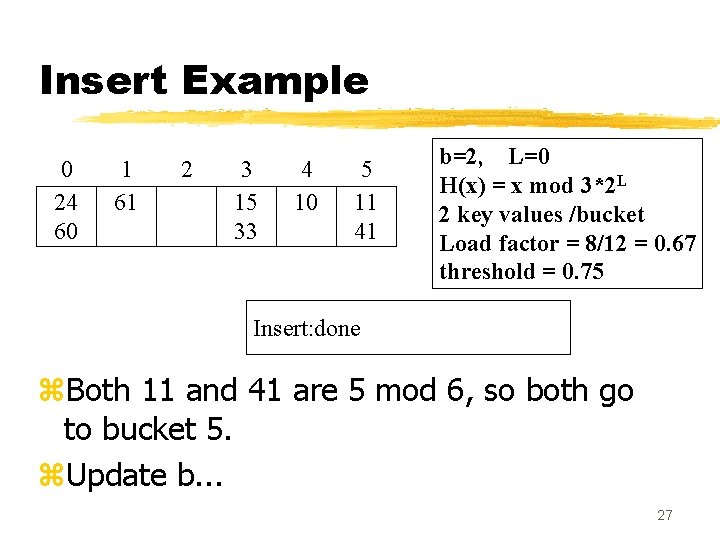
Insert Example 0 24 60 1 61 2 3 15 33 4 10 5 11 41 b=2, L=0 H(x) = x mod 3*2 L 2 key values /bucket Load factor = 8/12 = 0. 67 threshold = 0. 75 Insert: done z. Both 11 and 41 are 5 mod 6, so both go to bucket 5. z. Update b. . . 27
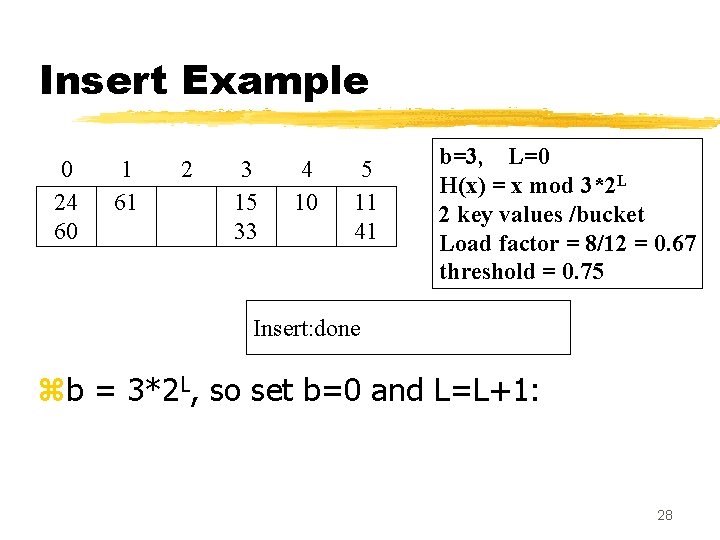
Insert Example 0 24 60 1 61 2 3 15 33 4 10 5 11 41 b=3, L=0 H(x) = x mod 3*2 L 2 key values /bucket Load factor = 8/12 = 0. 67 threshold = 0. 75 Insert: done zb = 3*2 L, so set b=0 and L=L+1: 28
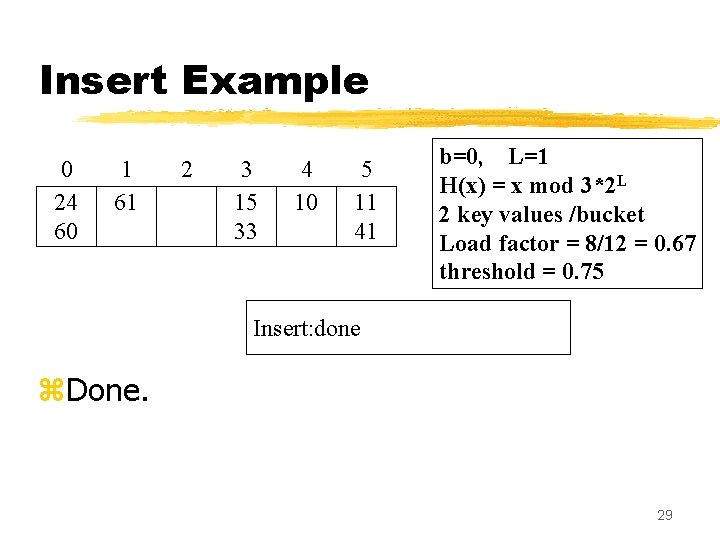
Insert Example 0 24 60 1 61 2 3 15 33 4 10 5 11 41 b=0, L=1 H(x) = x mod 3*2 L 2 key values /bucket Load factor = 8/12 = 0. 67 threshold = 0. 75 Insert: done z. Done. 29

Insert Example 0 24 60 1 61 2 62 3 15 33 4 10 5 11 41 30

Deleting with Extendible Hashing z. Delete works the opposite of insert: y. When the load factor goes below a lower threshold, combine buckets. y. Note: if b=0, it is necessary to decrement the level 31

Delete Algorithm z. Hash the key value to delete in the standard way, hashing at level L+1 if necessary. y. If the key value is not found, report failure and stop y. Else continue z. Update the load factor 32

Delete Algorithm II z. If the load factor <= Lower Threshold y. Decrement b yif (b== -1) xif (L=0) set b=0 and stop x. L=L-1 and b=n*2 L - 1 y. Combine the last bucket with bucket b; y. Repeat if necessary. 33
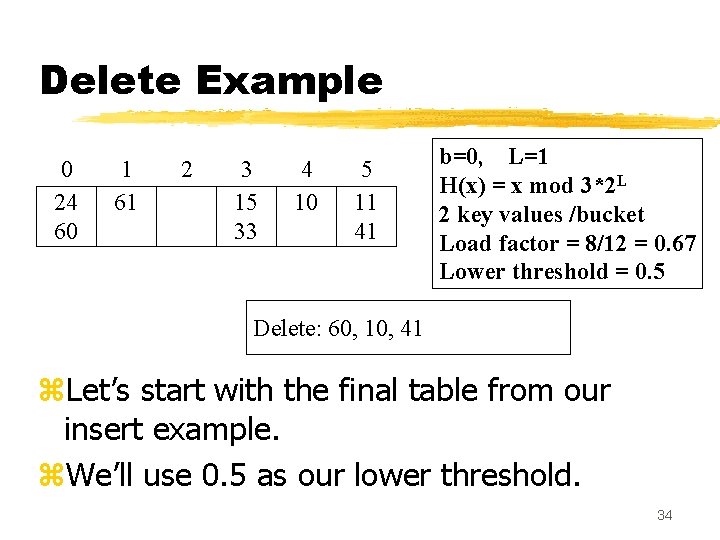
Delete Example 0 24 60 1 61 2 3 15 33 4 10 5 11 41 b=0, L=1 H(x) = x mod 3*2 L 2 key values /bucket Load factor = 8/12 = 0. 67 Lower threshold = 0. 5 Delete: 60, 10, 41 z. Let’s start with the final table from our insert example. z. We’ll use 0. 5 as our lower threshold. 34
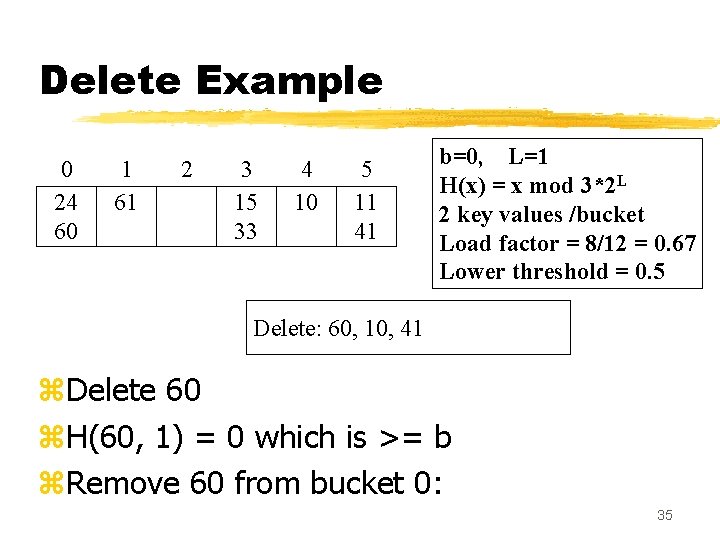
Delete Example 0 24 60 1 61 2 3 15 33 4 10 5 11 41 b=0, L=1 H(x) = x mod 3*2 L 2 key values /bucket Load factor = 8/12 = 0. 67 Lower threshold = 0. 5 Delete: 60, 10, 41 z. Delete 60 z. H(60, 1) = 0 which is >= b z. Remove 60 from bucket 0: 35
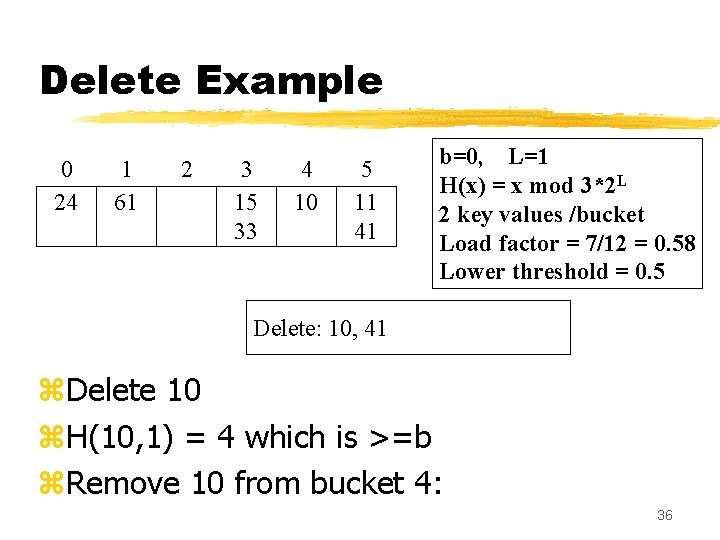
Delete Example 0 24 1 61 2 3 15 33 4 10 5 11 41 b=0, L=1 H(x) = x mod 3*2 L 2 key values /bucket Load factor = 7/12 = 0. 58 Lower threshold = 0. 5 Delete: 10, 41 z. Delete 10 z. H(10, 1) = 4 which is >=b z. Remove 10 from bucket 4: 36
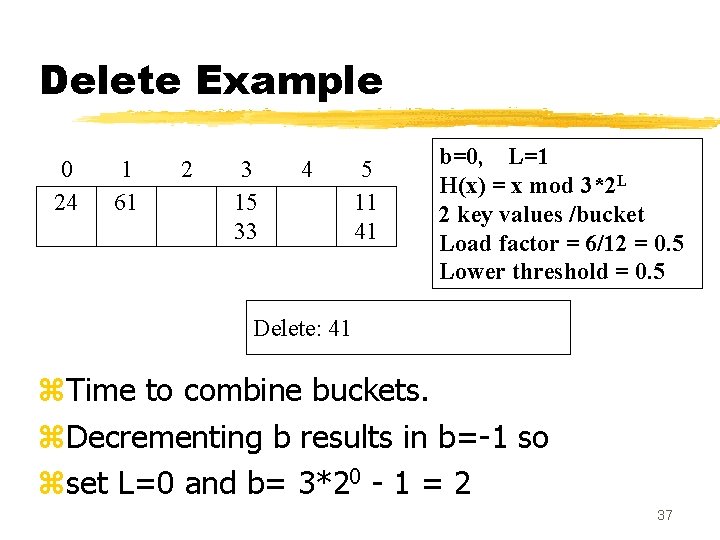
Delete Example 0 24 1 61 2 3 15 33 4 5 11 41 b=0, L=1 H(x) = x mod 3*2 L 2 key values /bucket Load factor = 6/12 = 0. 5 Lower threshold = 0. 5 Delete: 41 z. Time to combine buckets. z. Decrementing b results in b=-1 so zset L=0 and b= 3*20 - 1 = 2 37
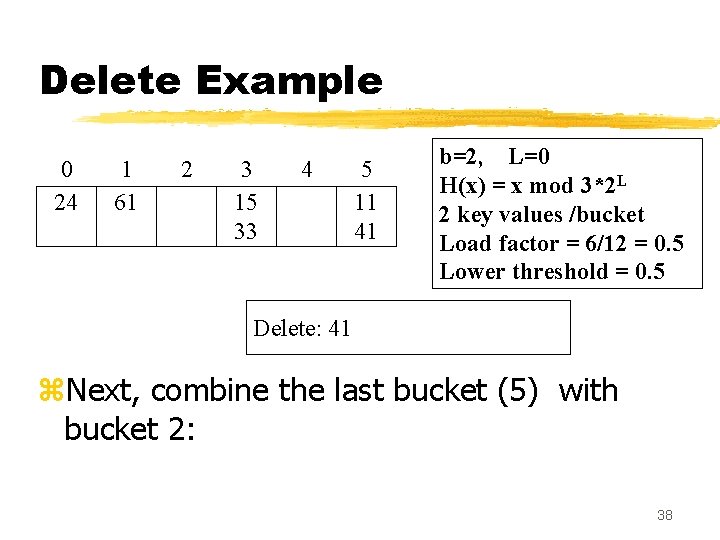
Delete Example 0 24 1 61 2 3 15 33 4 5 11 41 b=2, L=0 H(x) = x mod 3*2 L 2 key values /bucket Load factor = 6/12 = 0. 5 Lower threshold = 0. 5 Delete: 41 z. Next, combine the last bucket (5) with bucket 2: 38
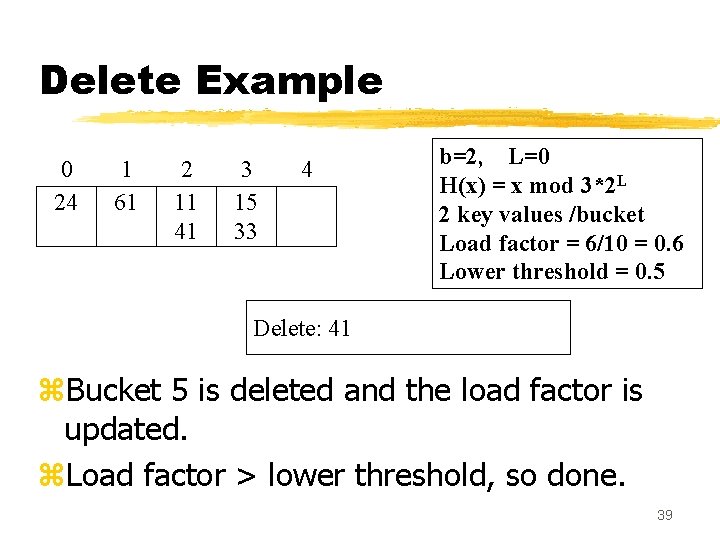
Delete Example 0 24 1 61 2 11 41 3 15 33 4 b=2, L=0 H(x) = x mod 3*2 L 2 key values /bucket Load factor = 6/10 = 0. 6 Lower threshold = 0. 5 Delete: 41 z. Bucket 5 is deleted and the load factor is updated. z. Load factor > lower threshold, so done. 39
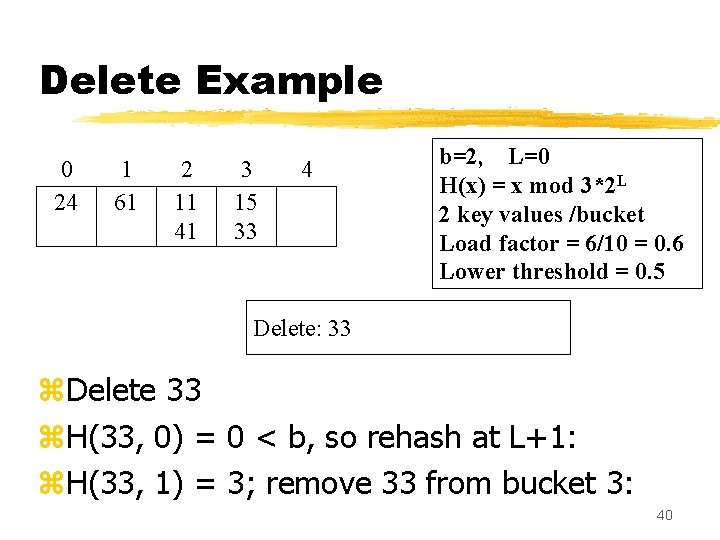
Delete Example 0 24 1 61 2 11 41 3 15 33 4 b=2, L=0 H(x) = x mod 3*2 L 2 key values /bucket Load factor = 6/10 = 0. 6 Lower threshold = 0. 5 Delete: 33 z. Delete 33 z. H(33, 0) = 0 < b, so rehash at L+1: z. H(33, 1) = 3; remove 33 from bucket 3: 40
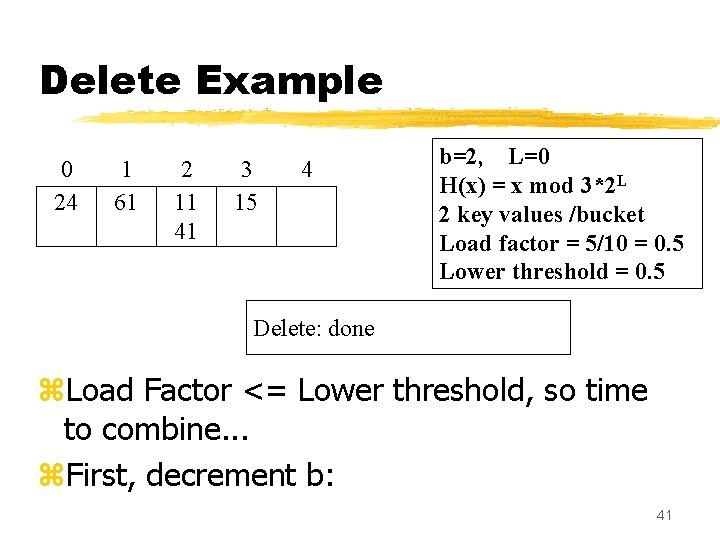
Delete Example 0 24 1 61 2 11 41 3 15 4 b=2, L=0 H(x) = x mod 3*2 L 2 key values /bucket Load factor = 5/10 = 0. 5 Lower threshold = 0. 5 Delete: done z. Load Factor <= Lower threshold, so time to combine. . . z. First, decrement b: 41
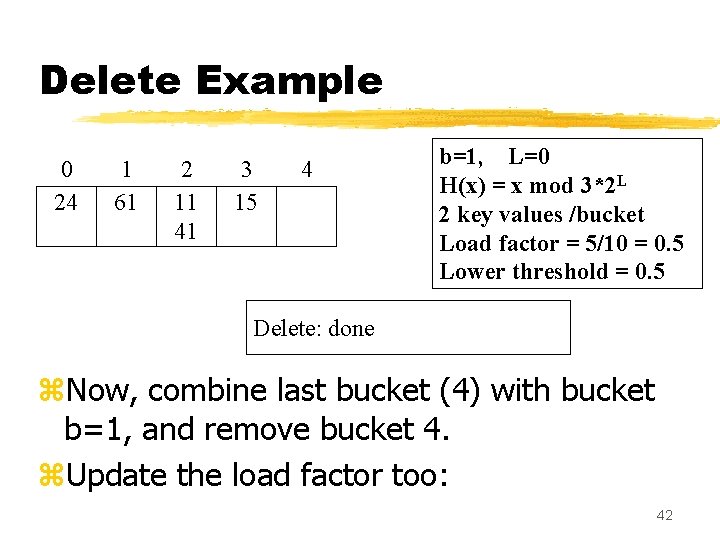
Delete Example 0 24 1 61 2 11 41 3 15 4 b=1, L=0 H(x) = x mod 3*2 L 2 key values /bucket Load factor = 5/10 = 0. 5 Lower threshold = 0. 5 Delete: done z. Now, combine last bucket (4) with bucket b=1, and remove bucket 4. z. Update the load factor too: 42
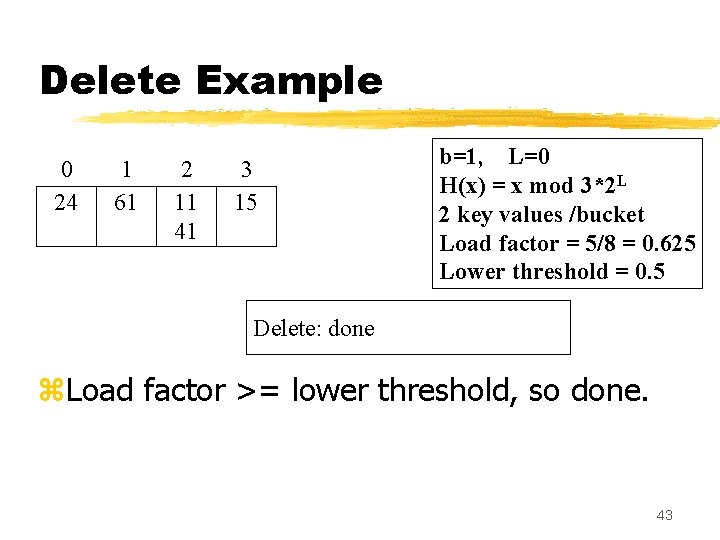
Delete Example 0 24 1 61 2 11 41 3 15 b=1, L=0 H(x) = x mod 3*2 L 2 key values /bucket Load factor = 5/8 = 0. 625 Lower threshold = 0. 5 Delete: done z. Load factor >= lower threshold, so done. 43
- Slides: 43