Extended Static Checking for Java Cormac Flanagan Joint
![Describing interfaces public class Vector { Object[] a; //@ invariant int size; //@ invariant](https://slidetodoc.com/presentation_image_h/75c52d93be13ee9561495d10145a2d23/image-10.jpg "Describing interfaces public class Vector { Object[] a; //@ invariant int size; //@ invariant")
![Verification condition generation q Easy for small languages [Dijkstra] q Much harder for real](https://slidetodoc.com/presentation_image_h/75c52d93be13ee9561495d10145a2d23/image-13.jpg "Verification condition generation q Easy for small languages [Dijkstra] q Much harder for real")
![Describing interfaces public Integer[] sum(Integer[] a, Integer[] b); //@ requires a != null &&](https://slidetodoc.com/presentation_image_h/75c52d93be13ee9561495d10145a2d23/image-37.jpg "Describing interfaces public Integer[] sum(Integer[] a, Integer[] b); //@ requires a != null &&")
- Slides: 37
Extended Static Checking for Java Cormac Flanagan Joint work with: Rustan Leino, Mark Lillibridge, Greg Nelson, Jim Saxe, and Raymie Stata Compaq Systems Research Center
What is “Static Checking”? Annotated Source Code Static Checker Error: . . . n type systems Error: wrong number of arguments in method call n lint Error: unreachable code n full program verification Error: qsort does not yield a sorted array
Why not just use testing? q Testing essential but n Expensive n Finds errors late n Misses errors q Static checking and testing complementary
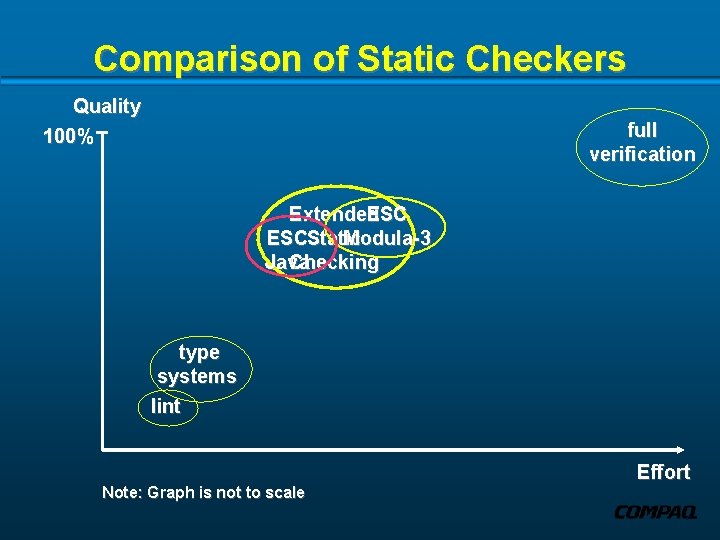
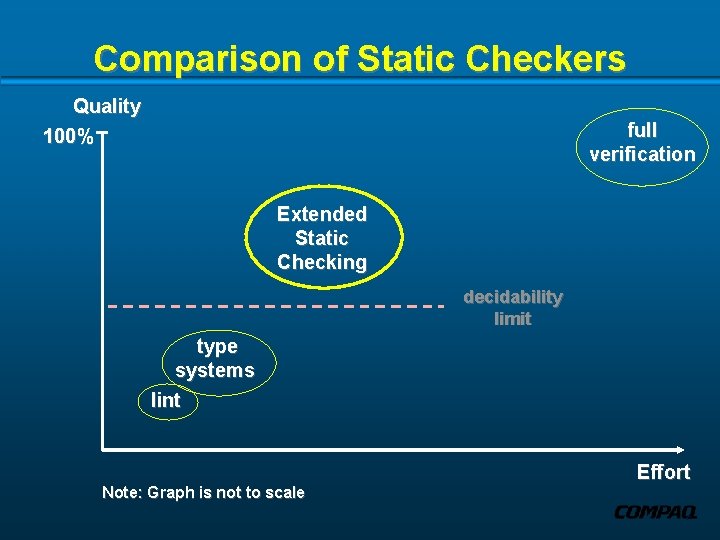
Comparison of Static Checkers Quality 100% full verification Extended ESCStatic Modula-3 Java Checking type systems lint Note: Graph is not to scale Effort
Goals of ESC/Java q Practical static checking q Detect common run-time errors n null dereferences n array bounds n type casts n race conditions n deadlocks n. . . q Modular checking
Non-goals of ESC/Java q Complete functional verification q Completeness n May not pass all programs q Soundness n May fail to detect errors n Error-resistant, not error-proof
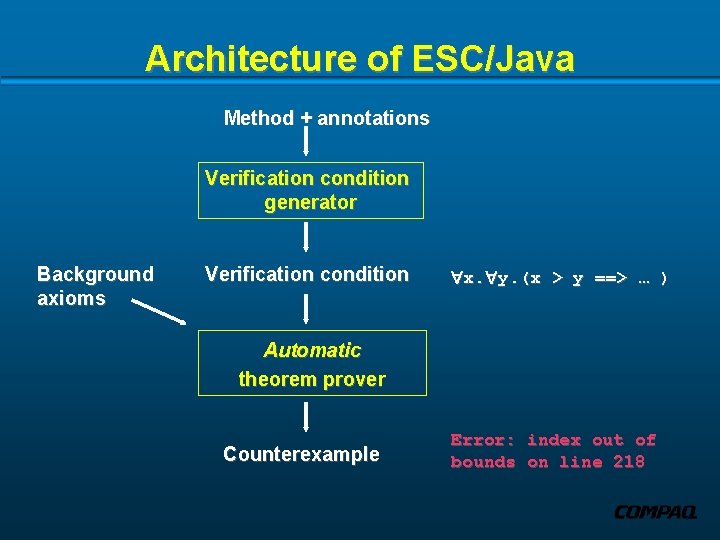
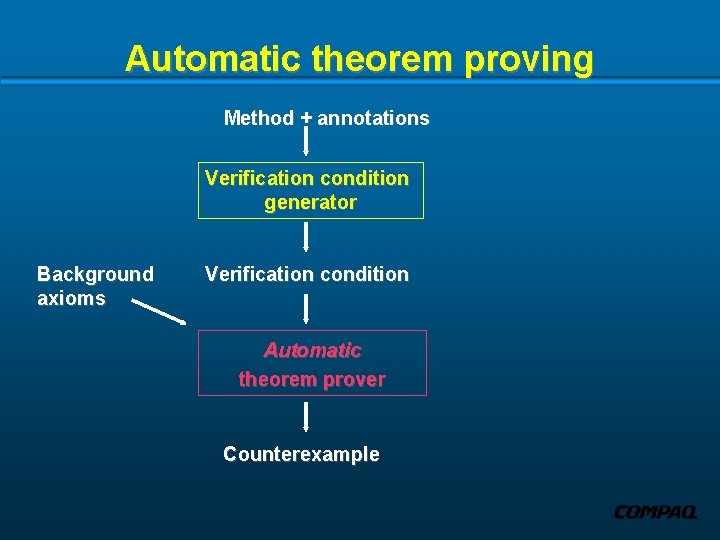
Architecture of ESC/Java Method + annotations Verification condition generator Background axioms Verification condition x. y. (x > y ==> … ) Automatic theorem prover Counterexample Error: index out of bounds on line 218
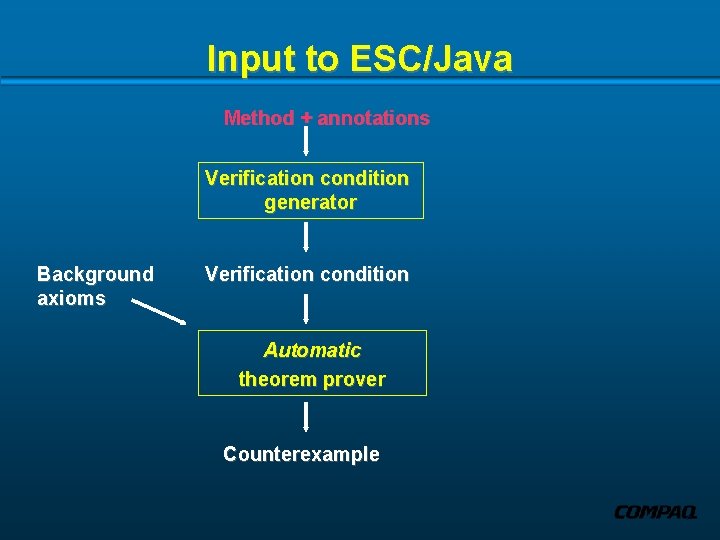
Input to ESC/Java Method + annotations Verification condition generator Background axioms Verification condition Automatic theorem prover Counterexample
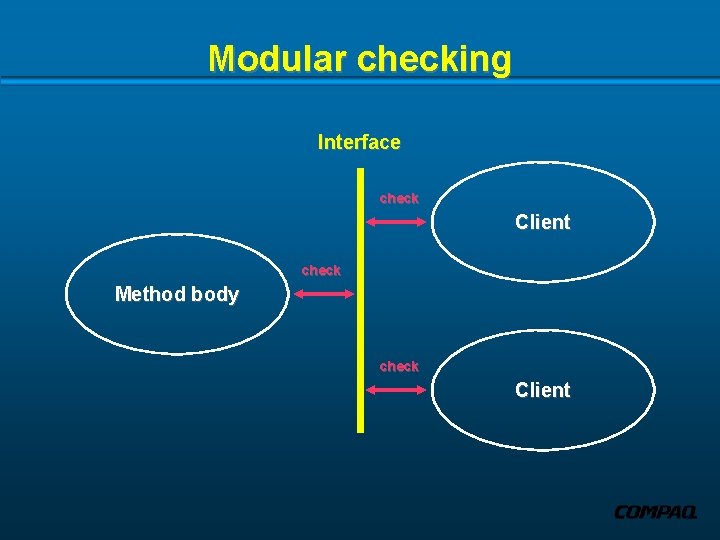
Modular checking Interface check Client check Method body check Client
Describing interfaces public class Vector { Object[] a; //@ invariant int size; //@ invariant a != null size <= a. length public Object element. At(int i) //@ requires 0 <= i && i < size {. . . } public Object[] copy. To. Array() //@ ensures RES != null && RES. length == size //@ modifies size, a[0], a[*] {. . . } }
Input to ESC/Java’s “checking engine” q Method implementation q Interface annotations n requires n ensures n modifies n invariants
Verification condition generation Method + annotations Verification condition generator Background axioms Verification condition Automatic theorem prover Counterexample
Verification condition generation q Easy for small languages [Dijkstra] q Much harder for real languages q Object-oriented q Typed q Dynamic allocation q Exceptions q Aliasing q Threads
Verification conditions for real programs Java Guarded command wlp Verification condition x = a[ i++ ]; assume preconditions assume invariants. . . i 0 = i; i = i + 1; assert (LABEL Null@218: a != null); assert (LABEL Index. Neg@218: 0 <= i 0); assert (LABEL Index. Too. Big@218: i 0 < a. length); x = elems[a][i 0]; . . . assert postconditions assert invariants i 0. (i 0 == i ==> … )
Exceptions q Java has exceptions q Add exceptions (raise and catch) to guarded command language q Calculate wlp of GC statement with respect to normal and exceptional postconditions
Method overriding q Method in subclass can override method in superclass n Must respect interface of overridden method n Weaker requires clause n Stronger ensures clause
Verification condition Method + annotations Verification condition generator Background axioms Verification condition Automatic theorem prover Counterexample
Verification condition q Formula in untyped, first-order predicate calculus n n n equality and function symbols quantifiers arithmetic operations select and store operations Eg. x. y. (x > y ==> … )
Example verification condition q Verification condition large but “dumb” (IMPLIES (DISTINCT | ec. Return| |L_14. 4|) (IMPLIES (AND (EQ |a@pre: 2. 8| |a: 2. 8|) (EQ |a: 2. 8| ( as. Field |a: 2. 8| (array |T_ int|))) (< (f. Closed. Time |a: 2. 8|) alloc) (EQ |n@pre: 3. 6| |n: 3. 6|) (EQ |n: 3. 6| ( as. Field |n: 3. 6| |T_int|)) (EQ |MAX_VALUE@pre: 3. 4. 26| |MAX_VALUE: 3. 4. 26|) (EQ |@true| (is |MAX_VALUE: 3. 4. 26| |T_ int|)) (EQ |elems@pre| elems) (EQ elems (as. Elems elems)) (< (e. Closed. Time elems ) alloc) (EQ LS (as. Lock. Set LS)) (EQ |alloc@pre| alloc) (EQ |@true| (is |this<1>| |T_Bag|)) (EQ |@true| (is. Allocated |this<1>| alloc)) (NEQ |this<1>| null)) (FORALL (tmp 1 |tmp 2: 21. 4| |tmp 3: 21. 6| |m: 12. 8| | mindex: 13. 8| |i: 14. 13| |tmp 0: 14. 28|) (AND (IMPLIES (<= 1 (select |n: 3. 6| |this<1>|)) (AND (LBLNEG |Null@15. 10~15. 10| (NEQ (select |a: 2. 8| |this<1>|) null)) (LBLNEG | Index. Negative@15. 10~15. 11| (<= 0 1)) (LBLNEG | Index. Too. Big@15. 10~15. 11| (< 1 ( array. Length (select |a: 2. 8| |this<1>|)))) (IMPLIES (< (select elems (select |a: 2. 8| |this<1>|)) 1) |MAX_VALUE: 3. 4. 26|) (AND (LBLNEG |Null@17. 12~17. 12| (NEQ (select |a: 2. 8| |this<1>|) null)) (LBLNEG | Index. Negative@17. 12~17. 13| (<= 0 1)) (LBLNEG |Index. Too. Big@17. 12~17. 13| (< 1 ( array. Length (select |a: 2. 8| |this<1>|)))) (FORALL (|m: 17. 8|) (IMPLIES (EQ |m: 17. 8| (select elems (select |a: 2. 8| |this<1>|)) 1)) (FORALL (|i: 14. 28|) (IMPLIES (AND (EQ |i: 14. 28| (+ 1 1)) (EQ |@true| | bool$false|)) (FORALL (|tmp 2: 21. 4<1>|) (IMPLIES (EQ |tmp 2: 21. 4<1>| (select |a: 2. 8| |this<1>|)) (AND (LBLNEG |Null@21. 16~21. 16| (NEQ (select |a: 2. 8| |this<1>|) null)) (LBLNEG | Index. Negative@21. 16~21. 17| (<= 0 (select (store |n: 3. 6| |this<1>| (- (select |n: 3. 6| |this<1>|) 1)) |this<1>|))) (LBLNEG | Index. Too. Big@21. 16~21. 17| (< (select (store |n: 3. 6| |this<1>| (- (select |n: 3. 6| |this<1>|) 1)) |this<1>|) ( array. Length (select |a: 2. 8| |this<1>|)))) (LBLNEG |Null@21. 4~21. 4| (NEQ |tmp 2: 21. 4<1>| null)) (LBLNEG |Index. Negative@21. 4~21. 5| (<= 0 1)) (LBLNEG | Index. Too. Big@21. 4~21. 5| (< 1 ( array. Length |tmp 2: 21. 4<1>|))) (LBLNEG |Exception: 11. 6~11. 6@11. 2~11. 2| (EQ | ec. Return| |ec. Return|)))))) (IMPLIES (NOT (< (select elems (select |a: 2. 8| |this<1>|)) 1) |MAX_VALUE: 3. 4. 26|)) (FORALL (|i: 14. 28|) (IMPLIES (AND (EQ |i: 14. 28| (+ 1 1)) (EQ |@true| | bool$false|)) (FORALL (|tmp 2: 21. 4<1>|) (IMPLIES (EQ |tmp 2: 21. 4<1>| (select |a: 2. 8| |this<1>|)) (AND (LBLNEG |Null@21. 16~21. 16| (NEQ (select |a: 2. 8| |this<1>|) null)) (LBLNEG | Index. Negative@21. 16~21. 17| (<= 0 (select (store |n: 3. 6| |this<1>| (- (select |n: 3. 6| |this<1>|) 1)) |this<1>|))) (LBLNEG | Index. Too. Big@21. 16~21. 17| (< (select (store |n: 3. 6| |this<1>| (- (select |n: 3. 6| |this<1>|) 1)) |this<1>|) (array. Length (select |a: 2. 8| |this<1>|)))) (LBLNEG |Null@21. 4~21. 4| (NEQ |tmp 2: 21. 4<1>| null)) (LBLNEG | Index. Negative@21. 4~21. 5| (<= 0 0)) (LBLNEG | Index. Too. Big@21. 4~21. 5| (< 0 ( array. Length |tmp 2: 21. 4<1>|))) (LBLNEG |Exception: 11. 6~11. 6@11. 2~11. 2| (EQ |ec. Return|))))) (IMPLIES (NOT (<= 1 (select |n: 3. 6| |this<1>|))) (AND (IMPLIES (EQ |L_14. 4|) (FORALL (|tmp 2: 21. 4<1>|) (IMPLIES (EQ |tmp 2: 21. 4<1>| (select |a: 2. 8| |this<1>|)) (AND (LBLNEG |Null@21. 16~21. 16| (NEQ (select |a: 2. 8| |this<1>|) null)) (LBLNEG | Index. Negative@21. 16~21. 17| (<= 0 (select (store |n: 3. 6| |this<1>| (- (select |n: 3. 6| |this<1>|) 1)) |this<1>|))) (LBLNEG | Index. Too. Big@21. 16~21. 17| (< (select (store |n: 3. 6| |this<1>| (- (select |n: 3. 6| |this<1>|) 1)) |this<1>|) (array. Length (select |a: 2. 8| |this<1>|)))) (LBLNEG |Null@21. 4~21. 4| (NEQ |tmp 2: 21. 4<1>| null)) (LBLNEG | Index. Negative@21. 4~21. 5| (<= 0 0)) (LBLNEG | Index. Too. Big@21. 4~21. 5| (< 0 ( array. Length |tmp 2: 21. 4<1>|))) (LBLNEG |Exception: 11. 6~11. 6@11. 2~11. 2| (EQ |ec. Return|)))))) (IMPLIES (NOT (EQ |L_14. 4|)) (AND (LBLNEG |Exception: 11. 6~11. 6@11. 2~11. 2| (EQ |L_14. 4| |ec. Return|)))))
Background axioms Method + annotations Verification condition generator Background axioms Verification condition Automatic theorem prover Counterexample
Background axioms q Additional properties of Java that theorem prover needs to know q A variable of type T always holds a value whose type is a subtype of T q The subtyping relation is reflexive, anti -symmetric, and transitive q new returns an object that is distinct from all existing objects q. . . lots more. . . q java. lang. Object has no supertype
Automatic theorem proving Method + annotations Verification condition generator Background axioms Verification condition Automatic theorem prover Counterexample
Automatic theorem proving q Use Simplify n Theorem prover from ESC/Modula-3 n Accepts formulae in untyped, first-order predicate calculus n Attempts to prove or refute
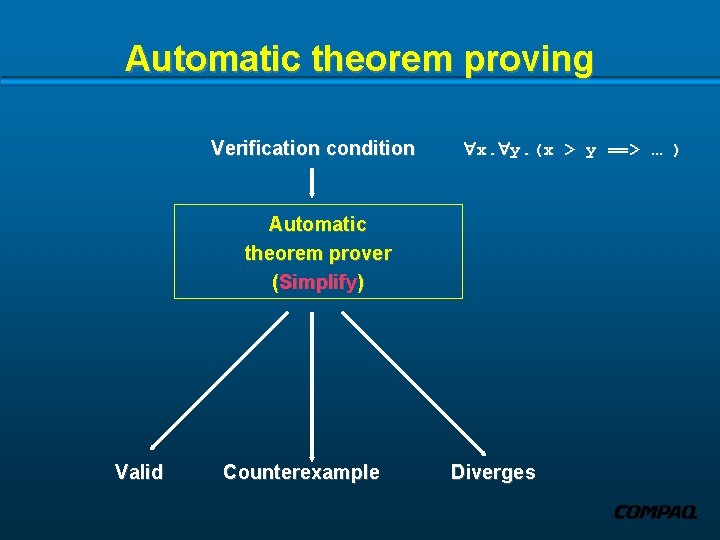
Automatic theorem proving Verification condition x. y. (x > y ==> … ) Automatic theorem prover (Simplify) Valid Counterexample Diverges
Handling counterexamples Method + annotations Verification condition generator Background axioms Verification condition Automatic theorem prover Counterexample
Error message from counterexample Verification condition x. y. ( … (LABEL Index. Too. Big@218 …) …) Automatic theorem prover (Simplify) Counterexample: x 417 > 7 … Label: Index. Too. Big@218 … Error: index out of bounds on line 218
Initial experience q First implementation is done q Run on 30, 000+ lines of code (mostly itself) q Caught several errors n null dereference, array bounds q Programmer can annotate and check about 300 lines per hour q Looks promising. . .
Demonstration
ESC/Java Summary q Finds more errors than type checking q Costs less than full verification q Currently working; is being evaluated q Potential as “software reliability metric” q Practical checking based on automatic theorem proving may be possible www. research. digital. com/SRC/esc/Esc. html
Comparison of Static Checkers Quality 100% full verification Extended Static Checking decidability limit type systems lint Note: Graph is not to scale Effort
Metrics for Static Checkers q Cost of using the tool q Quality Does it miss errors? Does it give spurious warnings?
Challenges q Automatic theorem proving q Error messages from counterexample q Verification conditions for real programs q Object-oriented q Typed q Dynamic allocation q Exceptions
ESC/Java vs. Testing q Testing essential but n Expensive n Finds errors late n Misses errors q ESC/Java. . . ?
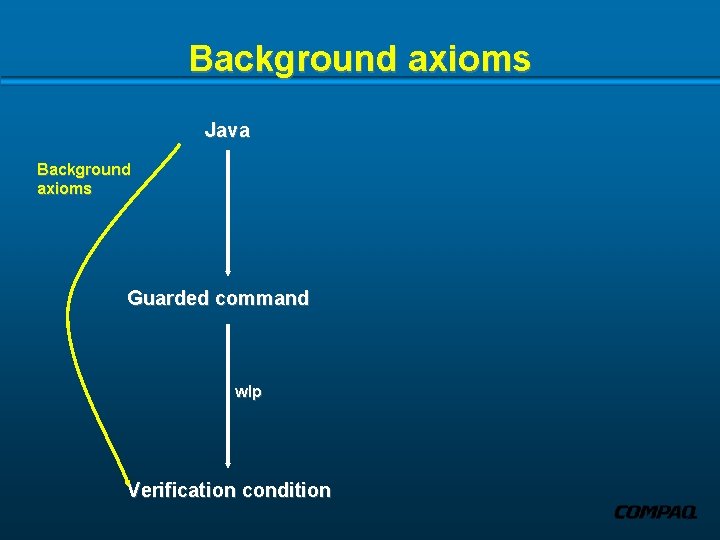
Background axioms Java Background axioms Guarded command wlp Verification condition
Additional annotations //@ assert <exp> //@ assume <exp> //@ nowarn <error code> //@ axiom <exp>
Describing interfaces public Integer[] sum(Integer[] a, Integer[] b); //@ requires a != null && b != null; //@ requires a. length == b. length; //@ ensures RES != null && RES. length == a. length; //@ modifies a[0], b[*];