Extended Introduction to Computer Science 1 Course Structure

Extended Introduction to Computer Science 1

Course Structure • Three Elements – Lectures ( )הרצאות – Recitations ( )תרגולים – Homework ( )תרגילי בית • Final Grade = Homework + Mid. Term Exam + Final Exam חובה להגיש ולקבל ציון 80% עובר עבור לפחות !! מהתרגילים 3

Computer Science 4

Geometry Giha Earth Metra Measure 5

Declarative Knowledge “What is true” 6

Imperative Knowledge “How to” To find an approximation of x: • Make a guess G • Improve the guess by averaging G and x/G • Keep improving the guess until it is good enough 7 [Heron of Alexandria]

To find an approximation of x: • Make a guess G • Improve the guess by averaging G and x/G • Keep improving the guess until it is good enough X=2 X/G = 2 G=1 G = ½ (1+ 2) = 1. 5 X/G = 4/3 G = ½ (3/2 + 4/3) = 17/12 = 1. 416666 X/G = 24/17 G = ½ (17/12 + 24/17) = 577/408 = 1. 4142156 8

“How to” knowledge Process – series of specific, mechanical steps for deducing information, based on simpler data and set of operations Procedure – particular way of describing the steps a process will evolve through Need a language for description: • vocabulary • rules for connecting elements – syntax • rules for assigning meaning to constructs – semantics 9

Designing Programs • Controlling Complexity – Black Box Abstraction – Conventional Interfaces – Meta-linguistic Abstraction 10

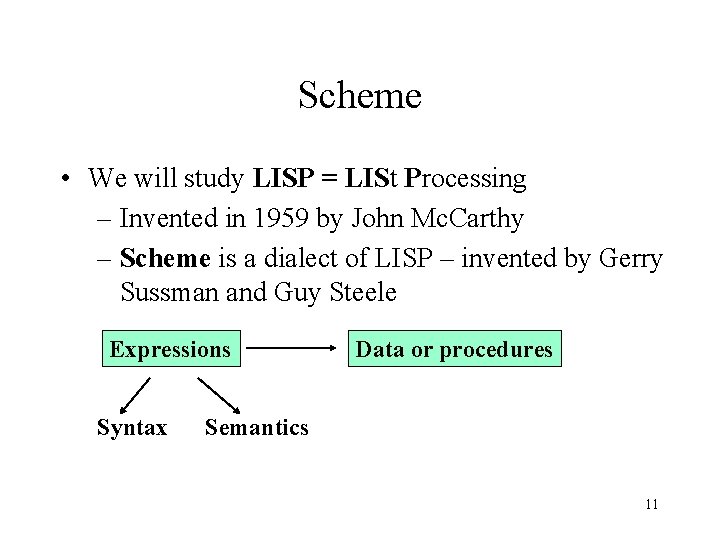
Scheme • We will study LISP = LISt Processing – Invented in 1959 by John Mc. Carthy – Scheme is a dialect of LISP – invented by Gerry Sussman and Guy Steele Expressions Syntax Data or procedures Semantics 11

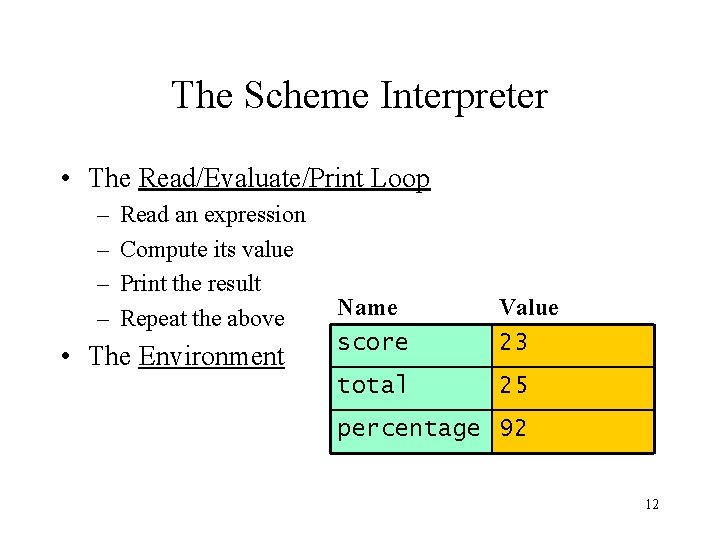
The Scheme Interpreter • The Read/Evaluate/Print Loop – – Read an expression Compute its value Print the result Repeat the above • The Environment Name score Value 23 total 25 percentage 92 12

Designing Programs • Controlling Complexity – Problem Decomposition – Black Box Abstraction • Implementation vs. Interface – Modularity 13

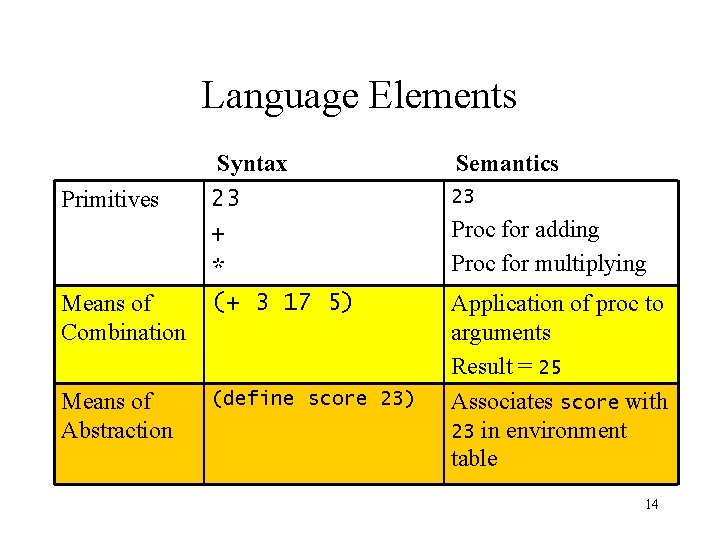
Language Elements Primitives Means of Combination Means of Abstraction Syntax 23 + * (+ 3 17 5) (define score 23) Semantics 23 Proc for adding Proc for multiplying Application of proc to arguments Result = 25 Associates score with 23 in environment table 14

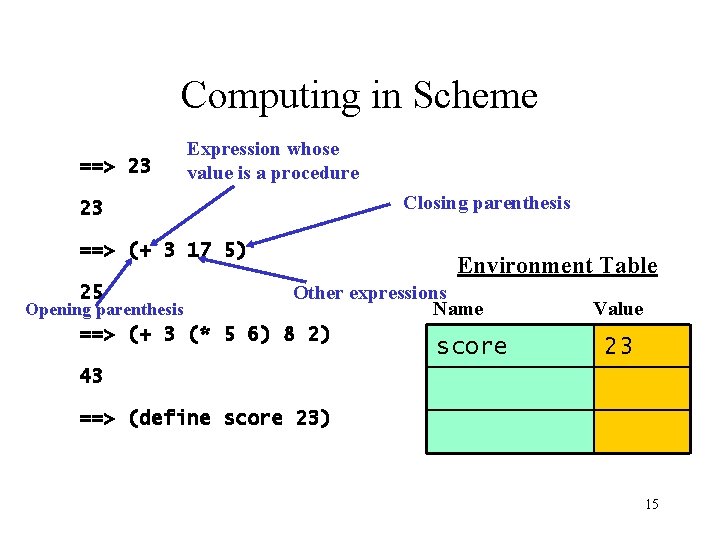
Computing in Scheme ==> 23 Expression whose value is a procedure 23 ==> (+ 3 17 5) Closing parenthesis Environment Table Other expressions Name Opening parenthesis ==> (+ 3 (* 5 6) 8 2) 25 score Value 23 43 ==> (define score 23) 15

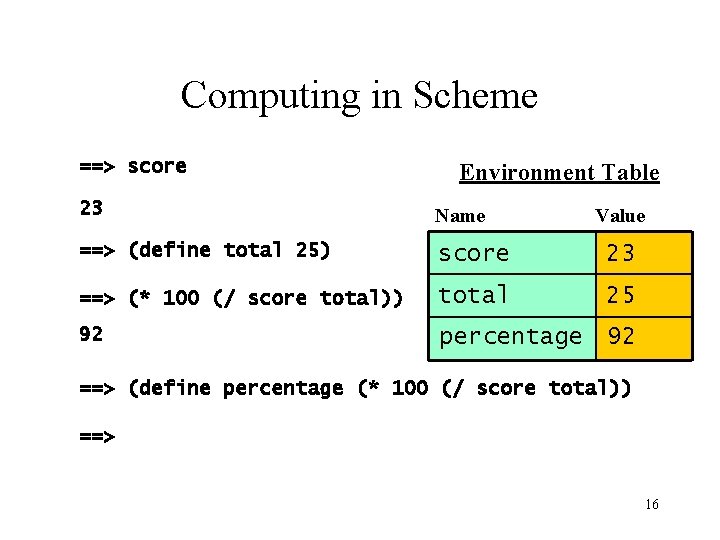
Computing in Scheme ==> score Environment Table 23 Name ==> (define total 25) score 23 ==> (* 100 (/ score total)) total 25 92 percentage 92 Value ==> (define percentage (* 100 (/ score total)) ==> 16

Evaluation of Expressions The value of a numeral: number The value of a built-in operator: machine instructions to execute The value of any name: the associated value in the environment To Evaluate a combination: (as opposed to special form) a. Evaluate all of the sub-expressions in some order b. Apply the procedure that is the value of the leftmost subexpression to the arguments (the values of the other subexpressions) 17

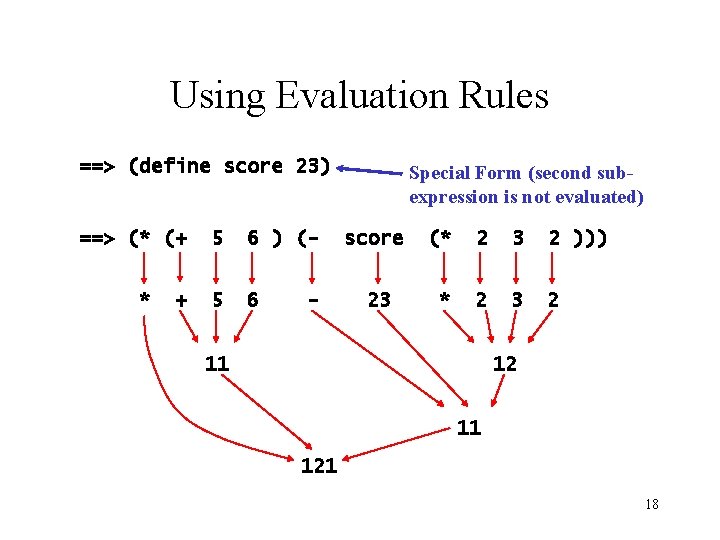
Using Evaluation Rules ==> (define score 23) ==> (* (+ * + 5 6 ) (- 5 6 - Special Form (second subexpression is not evaluated) score (* 2 3 2 ))) 23 * 2 3 2 11 121 18

Abstraction – Compound Procedures • How does one describe procedures? formal parameters • (lambda (x) (* x x)) body To process something multiply it by itself • Special form – creates a “procedure object” and returns it as a “value” Proc (x) (* x x) Internal representation 19

Lambda • The use of the word “lambda” is taken from lambda calculus. – Introduced in the Discrete Math course. – Useful notation for functions. 20

Evaluation of An Expression To Apply a compound procedure: (to a list of arguments) Evaluate the body of the procedure with the formal parameters replaced by the corresponding actual values ==> ((lambda(x)(* x x)) 5) Proc(x)(* x x) 5 (* 5 5) 25 21

Evaluation of An Expression The value of a numeral: number The value of a built-in operator: machine instructions to execute The value of any name: the associated object in the environment To Evaluate a combination: (other than special form) a. Evaluate all of the sub-expressions in any order b. Apply the procedure that is the value of the leftmost subexpression to the arguments (the values of the other subexpressions) To Apply a compound procedure: (to a list of arguments) Evaluate the body of the procedure with the formal parameters replaced by the corresponding actual values 22

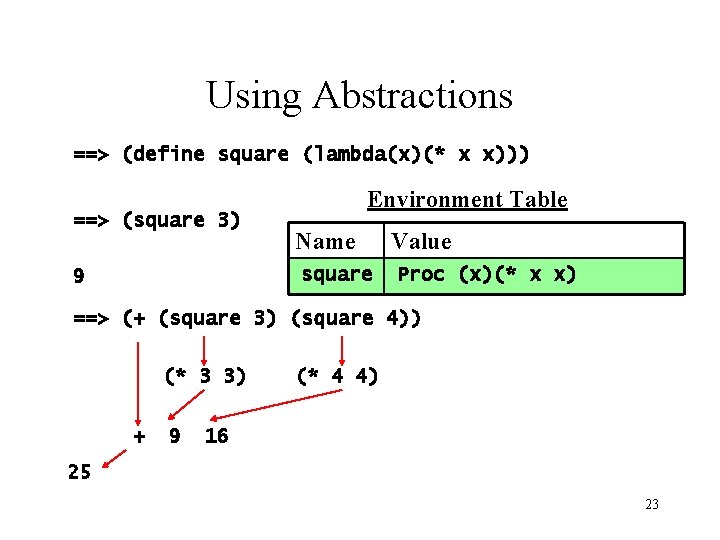
Using Abstractions ==> (define square (lambda(x)(* x x))) ==> (square 3) Environment Table Name square 9 Value Proc (x)(* x x) ==> (+ (square 3) (square 4)) (* 3 3) + 9 (* 4 4) 16 25 23

Yet More Abstractions ==> (define sum-of-two-squares (lambda(x y)(+ (square x) (square y)))) ==> (sum-of-two-squares 3 4) 25 ==> (define f (lambda(a) (sum-of-two-squares (+ a 3) (* a 3)))) Try it out…compute (f 3) on your own 24

Evaluation of An Expression (reminder) reduction The value of a numeral: number in lambda Substitution The value of a built-in operator: machine instructions to execute The value of any name: the associated object inmodel the environment calculus To Evaluate a combination: (other than special form) a. Evaluate all of the sub-expressions in any order b. Apply the procedure that is the value of the leftmost subexpression to the arguments (the values of the other subexpressions) To Apply a compound procedure: (to a list of arguments) Evaluate the body of the procedure with the formal parameters substituted by the corresponding actual values 25

Let’s Not Forget The Environment ==> (define x 8) ==> (+ x 1) 9 ==> (define x 5) ==> (+ x 1) 6 The value of (+ x 1) depends on the environment! 26

Using the substitution model (define square (lambda (x) (* x x))) (define average (lambda (x y) (/ (+ x y) 2))) (average 5 (square 3)) (average 5 (* 3 3)) (average 5 9) first evaluate operands, then substitute (/ (+ 5 9) 2) (/ 14 2) if operator is a primitive procedure, 7 replace by result of operation 27

Booleans Two distinguished values denoted by the constants #t and #f The type of these values is boolean ==> (< 2 3) #t ==> (< 4 3) #f 28

Values and types In scheme almost every expression has a value Examples: 1) The value of 23 is 23 2) The value of + is a primitive procedure for addition 3) The value of (lambda (x) (* x x)) is the compound procedure proc (x) (* x x) Values have types. For example: 1) 2) 3) 4) The type of 23 is numeral The type of + is a primitive procedure The type of proc (x) (* x x) is a compound procedure The type of (> x 1) is a boolean (or logical) 29

No Value? • In scheme almost every expression has a value • Why almost? Example : what is the value of the expression (define x 8) • In scheme, the value of a define expression is “undefined”. This means “implementation-dependent” • Dr. Scheme does not return (print) any value for a define expression. • Other interpreters may act differently. 30

More examples ==> (define x 8) ==> (define x (* x 2)) ==> x 16 ==> (define x y) Environment Table Name Value x 16 8 + #<-> reference to undefined identifier: y ==> (define + -) ==> (+ 2 2) 0 31

The IF special form (if <predicate> <consequent> <alternative>) If the value of <predicate> is #t, Evaluate <consequent> and return it Otherwise Evaluate <alternative> and return it (if (< 2 3) ==> 2 (if (< 2 3) 2 (/ 1 0)) ==> ERROR 2 32

IF is a special form • In a general form, we first evaluate all arguments and then apply the function • (if <predicate> <consequent> <alternative>) is different: <predicate> determines whether we evaluate <consequent> or <alternative>. We evaluate only one of them ! 33

Syntactic Sugar for naming procedures Instead of writing: (define square (lambda (x) (* x x)) We can write: (define (square x) (* x x)) 34

Some examples: (define twice ) (lambda (x) (* 2 x)) (twice 2) ==> 4 (twice 3) ==> 6 Using “syntactic sugar”: (define (twice x) (* 2 x)) (define second (lambda (x y z) y) ) (second 2 15 3) ==> 15 (second 34 -5 16) ==> -5 Using “syntactic sugar”: (define (second x y z) y) 35

Summary • Computer science formalizes the computational process • Programming languages are a way to describe this process • Syntax • Sematics • Scheme is a programming language whose syntax is structured around compound expressions • We model the semantics of the scheme via the substitution model, the mathematical equivalent of lambda calculus 36