Extended Euclidean Algorithm for multiplicative inverses mod m








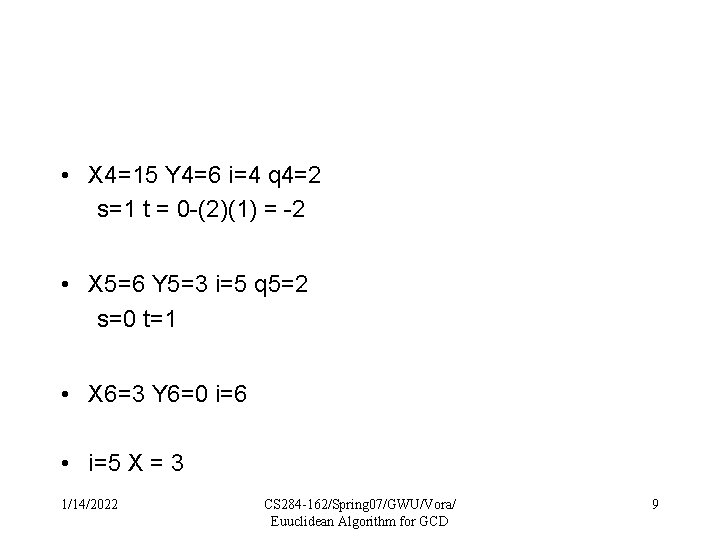


- Slides: 11

Extended Euclidean Algorithm for multiplicative inverses mod m CSCI 284/162 Spring 2007 GWU CS 284 -162/Spring 07/GWU/Vora/ Euuclidean Algorithm for GCD

Extended Euclidean algorithm Find s, t such that gcd(m, a) = sm +ta Let gcd(Xi, Yi) = si. Xi + ti. Yi (we have not shown that this is possible for any value of the gcd, though we have shown it to be true when the gcd is 1. Assume it is true for all values of the gcd) 1/14/2022 CS 284 -162/Spring 07/GWU/Vora/ Euuclidean Algorithm for GCD 2

Extended Euclidean algorithm Find s, t such that gcd(m, a) = sm +ta Let gcd(X, Y)i = si. Xi + ti. Yi 1. Last but one step: YN-1|XN-1 gcd(XN-1, YN-1) = YN-1 s. N-1=0; t. N-1=1 2. In general: If gcd(X, Y)i = si. Xi + ti. Yi What is: si-1 ti-1? 1/14/2022 CS 284 -162/Spring 07/GWU/Vora/ Euuclidean Algorithm for GCD 3

Extended Euclidean algorithm si. Xi + ti. Yi = si. Yi-1 + ti(Xi-1 – Yi-1*qi-1) = ti. Xi-1 + (si – ti*qi-1) Yi-1 So, si-1 = ti and ti-1 = si – ti*qi-1 Go back up the euclidean algorithm: (s, t) : = (0, 1) /* Initialize */ (s, t) : = (t, s-t*q) return((s, t)) 1/14/2022 CS 284 -162/Spring 07/GWU/Vora/ Euuclidean Algorithm for GCD 4

Examples gcd(17, 101) gcd(57, 93) What good? Write algorithm for multiplicative inverse of a mod m 1/14/2022 CS 284 -162/Spring 07/GWU/Vora/ Euuclidean Algorithm for GCD 5

Extended Euclidean algorithm Part I: Keep track of the quotient: i : = 0; (X 0, Y 0) : = (m, n) /* Initialize */ while (Yi 0) { qi : = Xi/Yi (Xi+1, Yi+1) : = (Yi, Xi – Yi*qi) i: = i+1 } i : = i-1 X = Yi 1/14/2022 CS 284 -162/Spring 07/GWU/Vora/ Euuclidean Algorithm for GCD 6

Extended Euclidean algorithm Part II: Go back up the euclidean algorithm: (s, t) : = (0, 1) /* Initialize */ while (i 0) { i : = i-1 (s, t) : = (t, s – t*q) } return(X, (s, t) ) 1/14/2022 CS 284 -162/Spring 07/GWU/Vora/ Euuclidean Algorithm for GCD 7

(93, 57) • X 0=93 Y 0=57 i=0 q 0=1 • X 1=57 Y 1=36 i=1 q 1=1 • X 2=36 Y 2=21 i=2 q 2=1 • X 3=21 Y 3=15 i=3 q 3=1 1/14/2022 CS 284 -162/Spring 07/GWU/Vora/ Euuclidean Algorithm for GCD 8
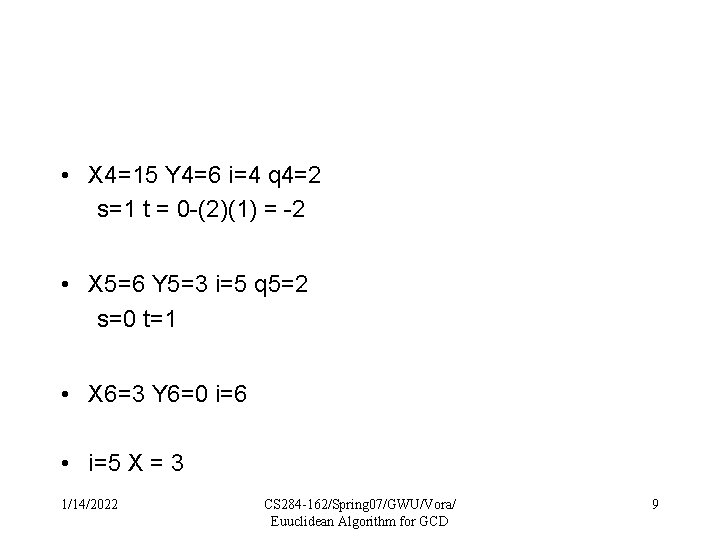
• X 4=15 Y 4=6 i=4 q 4=2 s=1 t = 0 -(2)(1) = -2 • X 5=6 Y 5=3 i=5 q 5=2 s=0 t=1 • X 6=3 Y 6=0 i=6 • i=5 X = 3 1/14/2022 CS 284 -162/Spring 07/GWU/Vora/ Euuclidean Algorithm for GCD 9

8 93 + (-13) 57 = 3 • X 0=93 Y 0=57 i=0 q 0=1 s=8 t=-5 -(8)(1)=-13 • X 1=57 Y 1=36 i=1 q 1=1 s=-5 t=3 -(-5)(1)=8 • X 2=36 Y 2=21 i=2 q 2=1 s=3 t=-2 -(1)(3)=-5 • X 3=21 Y 3=15 i=3 q 3=1 s=-2 t=1 -(-2)(1)=3 1/14/2022 CS 284 -162/Spring 07/GWU/Vora/ Euuclidean Algorithm for GCD 10

Euclidean Algorithm: References See Text, section 5. 2. 1 1/14/2022 CS 284 -162/Spring 07/GWU/Vora/ Euuclidean Algorithm for GCD 11