Expressions and Equations 5 5 Simplify Algebraic Expressions

Expressions and Equations 5. 5 Simplify Algebraic Expressions Learning Objectives • To identify the parts of an algebraic expression • To write an algebraic expression in simplest form by combining like terms Course 2, Lesson 5 -5

Expressions and Equations • • Course 2, Lesson 5 -5 term like terms constant simplest form

Step-by-Step Example 1. Identify the terms, like terms, coefficients, and constants in the expression 6 n – 7 n – 4 + n. 1 6 n – 7 n – 4 + n = 6 n + (– 7 n) + (– 4) + 1 n 2 • Terms: 6 n, – 7 n, – 4, n • Like terms: 6 n, – 7 n, n 3 Rewrite the expression. All of these terms have the same variable. • Coefficients: 6, – 7, 1 • Constants: – 4 This is the only term without a variable. Need Another Example?

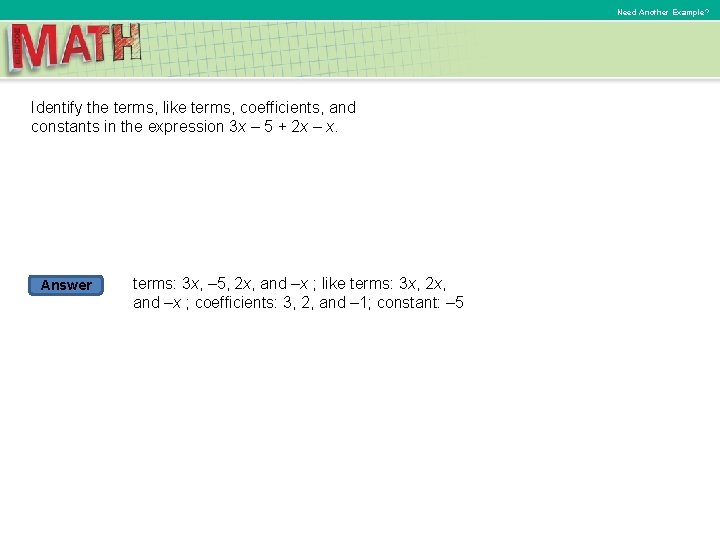
Need Another Example? Identify the terms, like terms, coefficients, and constants in the expression 3 x – 5 + 2 x – x. Answer terms: 3 x, – 5, 2 x, and –x ; like terms: 3 x, 2 x, and –x ; coefficients: 3, 2, and – 1; constant: – 5

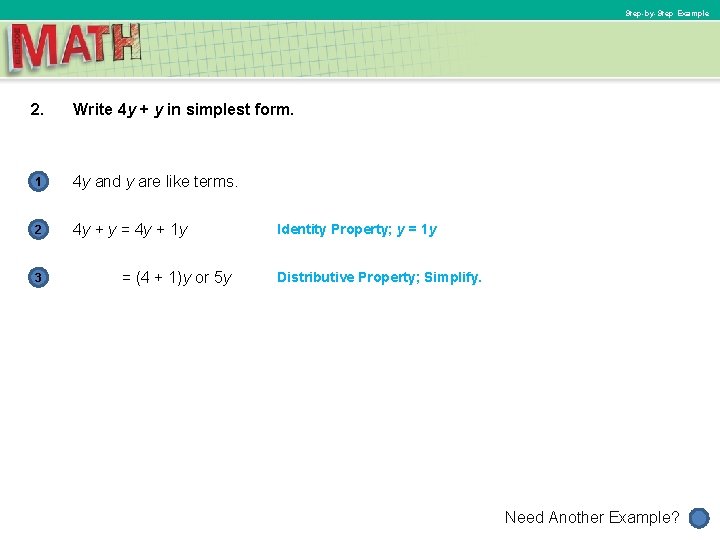
Step-by-Step Example 2. Write 4 y + y in simplest form. 1 4 y and y are like terms. 2 4 y + y = 4 y + 1 y 3 = (4 + 1)y or 5 y Identity Property; y = 1 y Distributive Property; Simplify. Need Another Example?

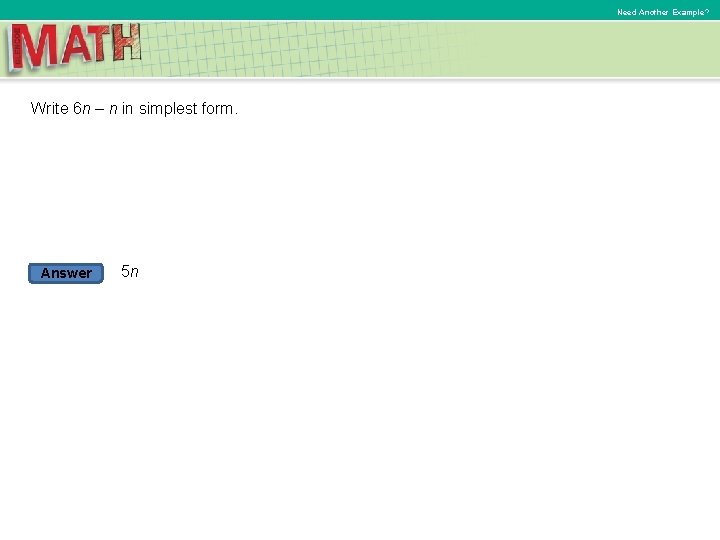
Need Another Example? Write 6 n – n in simplest form. Answer 5 n

Step-by-Step Example 3. Write 7 x – 2 – 7 x + 6 in simplest form. 1 7 x and – 7 x are like terms. – 2 and 6 are also like terms. 2 7 x – 2 – 7 x + 6 = 7 x + (– 2) + (– 7 x) + 6 3 = 7 x + (– 7 x) + (– 2) + 6 Commutative Property 4 = [7 + (– 7)]x + (– 2) + 6 Distributive Property 5 = 0 x + 4 Simplify. 6 = 0 + 4 or 4 Multiplicative Property of zero and Additive Identity Property of zero. Definition of subtraction Need Another Example?

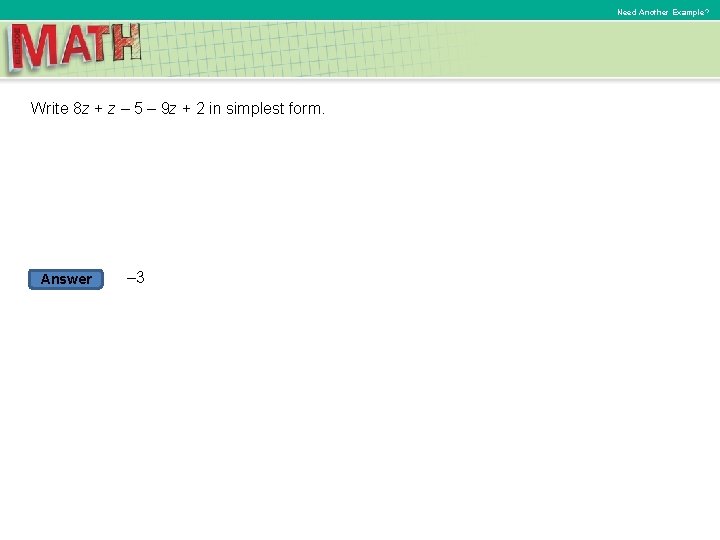
Need Another Example? Write 8 z + z – 5 – 9 z + 2 in simplest form. Answer – 3

Step-by-Step Example 4. 1 The cost of a jacket j after a 5% markup can be represented by the expression j + 0. 05 j. Simplify the expression. Then determine the total cost of the jacket after the markup, if the original price is $35. j + 0. 05 j = 1 j + 0. 05 j Identity Property; j = 1 j 2 = (1 + 0. 05)j Distributive Property 3 = 1. 05 j Simplify. 4 1. 05 j = 1. 05(35) 5 = 36. 75 6 Replace j with 35 to find the total cost. Multiply. So, the cost of the jacket after a 5% markup is $36. 75. Need Another Example?

Need Another Example? The cost of a set of DVDs after a 25% markup can be represented by the expression c + 0. 25 c. Simplify the expression. Then determine the total cost of the DVDs after the markup if the original price is $40. Answer 1. 25 c ; $50

Step-by-Step Example 5. At a concert, you buy some T-shirts for $12. 00 each and the same number of CDs for $7. 50 each. Write an expression in simplest form that represents the total amount spent. 1 Let x represent the number of T-shirts and CDs. 2 12 x + 7. 50 x Write the expression. 3 12 x + 7. 50 x = (12 + 7. 50)x Distributive Property 4 5 = 19. 50 x Simplify. The expression $19. 50 x represents the total amount spent. Need Another Example?

Need Another Example? Manfred buys some boxes of cereal for $4. 85 each and the same number of bags of pretzels for $2. 90 each. Write an expression in simplest form that represents the total amount spent. Answer 7. 75 x