EXPRESSES NUMRICAS Claudia Lisete Oliveira Groenwald 1 Expresses

EXPRESSÕES NUMÉRICAS Claudia Lisete Oliveira Groenwald 1

Expressões Numéricas são expressões matemáticas com uma sequência de operações numéricas (números associados por operações). Exemplos 2 x 5 +7 = 5+7 x 5= 8 : 4 – 6: 3 = 8– 4: 2= (3 + 5) : 2= 3+6: 2= 36 : 6 – (5 + 6)= 2

- As expressões que apresentem apenas adições e subtrações são resolvidas na ordem que aparecem; - Se em uma expressão houver parênteses, o cálculo deve começar pelas operações contidas dentro dele; - Em expressões que apresentem somas, subtrações, multiplicações, divisões, potência e raízes devem ser resolvidas obedecendo a sequência: 1º potenciação e radiciação na ordem que aparecem; 2º multiplicações e divisões na ordem que aparecem; 3º adições e subtrações na ordem que aparecem. - Em expressões que apresentem parênteses, colchetes e chaves deve-se eliminar (resolvendo as operações que estão dentro dos mesmos): 1º parênteses; 2º chaves; 3 3º colchetes.

Sobre a mesa há 12 pirulitos e dois pacotes com 50 mpirulitos em cada pacote. Quantoos pirulitos há sobre a mesa? 4

Sobre a mesa há 12 pirulitos e dois pacotes com 50 mpirulitos em cada pacote. Quantoos pirulitos há sobre a mesa? 12 + 2 x 50 = 12 + 100 = 112 pirulitos 5

Em uma sala de aula há 36 classes, chegaram 17 alunos no início da aula, cinco minutos depois chegaram mais 10 alunos. Quantas classes estão vazias? 36 – (17 + 10) = 36 – 27 = 9 classes vazias 6

Exemplo: Sabendo que uma caixa de cerveja possui 24 garrafas e uma caixa de refrigerantes possui 12 garrafas, resolva: - Compramos 8 caixas de cervejas e 5 caixas de refrigerantes. Quantas garrafas compramos no total? 8 x 24 + 5 x 12 = 192 + 60 = 252 -Foram utilizadas em uma festa 36 cervejas e 42 refrigerantes. Quantas garrafas sobraram? 252 – (36 + 42) = 252 – 78 = 174 -Escreva a expressão completa, usando todas as informações ao mesmo tempo. -8 x 24 + 5 x 12 - (36 + 42) = 174 7

Números e suas representações A ideia do número surgiu da necessidade de fazer contagens (mais tarde também medições). A correspondência um-a-um se mostrou inadequada para grandes quantidades. O número é a qualidade que as coleções têm, que dependem apenas da quantidade de seus elementos, independente da natureza dos objetos. Quando duas coleções apresentam a mesma quantidade de objetos, associamos a elas um mesmo número. Representamos os números gráfica e oralmente através de símbolos (os chamados numerais). Os numerais foram desenvolvidos a partir, principalmente do ato de agrupar. 8

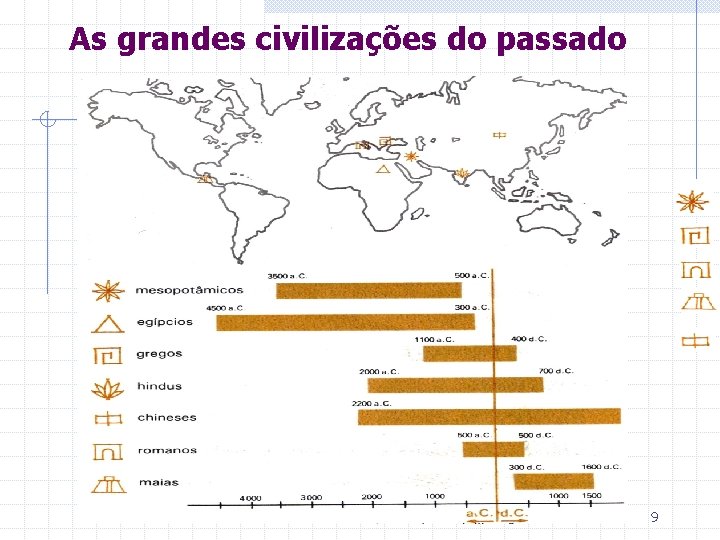
As grandes civilizações do passado 9

Os egípcios e os seus hieróglifos 5 000 anos atrás. Pirâmides (demonstravam o conhecimento avançado do povo). Construção, agricultura, astronomia, medicina, esculturas, entre outros. Inventaram uma forma de comunicação escrita e desenvolveram um sistema de numeração. Escrita hieróglifos (centenas de sinais complicados). Papel utilizado Papiro 10

Sistema de numeração egípcio sinais convencionais Cada símbolo representa dez vezes o que o símbolo anterior representa. 11

Observe a representação de alguns números: Observe a adição realizada pelos egípcios: Qual seria a representação do resultado? 12

Os números na Mesopotâmia Próximo ao Egito. Significa: região entre rios (Tigre e Eufrates). Rica em argila. Forma própria de escrever. Escreviam no barro. Imprimiam sinais em tabletes de barro. Caracteres em forma de cunha – cuneiformes. 13

Os números na escrita cuneiforme (até o número 59) 14

E o número 60? Para representar o número 2 as cunhas ficavam juntas. Para representar o número 61 eram separadas por um pequeno espaço. A troca é feita de sessenta em sessenta – base 60 – sexagesimal 15

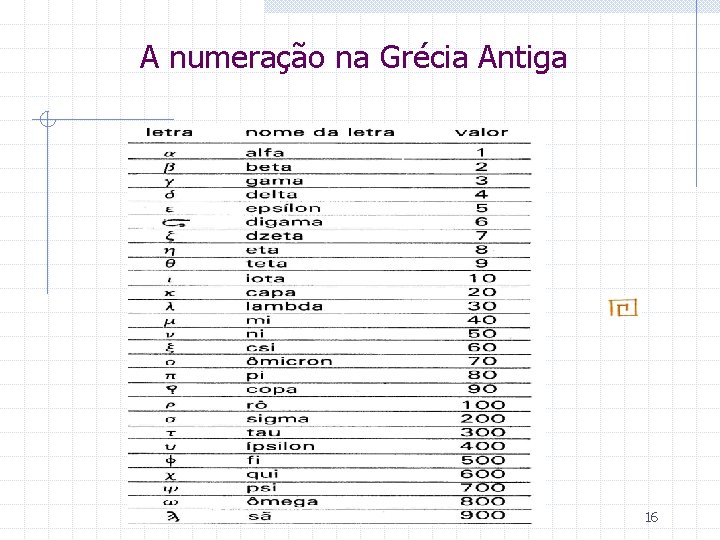
A numeração na Grécia Antiga 16

A civilização romana Península Itálica. Uma das mais importantes do mundo antigo. Venceram guerras (conquista de novos territórios). Roma: fundada em 753 a. C. Centro de atividades culturais. 17

O sistema de numeração romana Se parece com o sistema egípcio. Base dez. A letra a esquerda do valor maior é subtraída. A letra a direita do valor maior é adicionada. Mil vezes mais é representado por um traço sobre a letra. Até hoje esse sistema é utilizado. O sistema egípcio era apenas aditivo, enquanto o sistema romano é aditivo e subtrativo. 18

19

A civilização dos MAIAS 1 600 anos atrás. Durante mais de 10 000 anos habitaram a região onde hoje se localiza o sul do México e a América central. Povos indígenas de cultura avançada. Até 300 os números eram agrupados de vinte em vinte. 20

O sistema de numeração dos Maias Um ponto valia um e um traço valia cinco. 21

Os chineses Foi um dos primeiros povos a construir uma grande civilização. Há mais de 3 000 anos já sabiam irrigar campos e produzir alimentos. Tecidos de seda. Escreviam usando figuras como sinais. 22

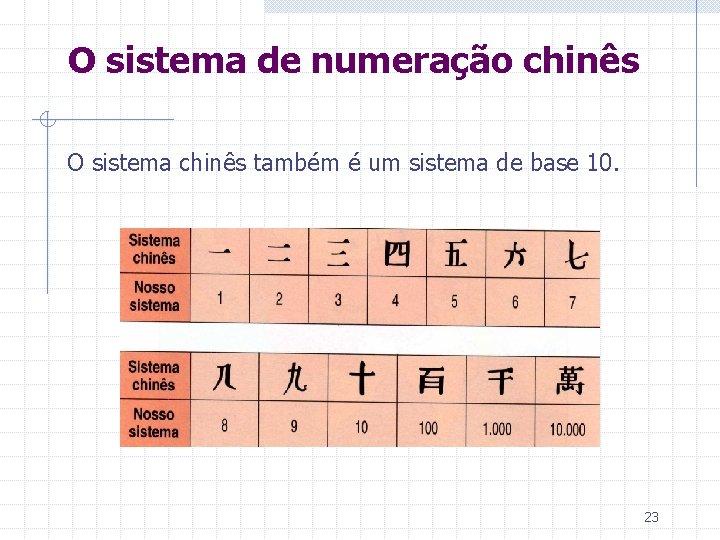
O sistema de numeração chinês O sistema chinês também é um sistema de base 10. 23

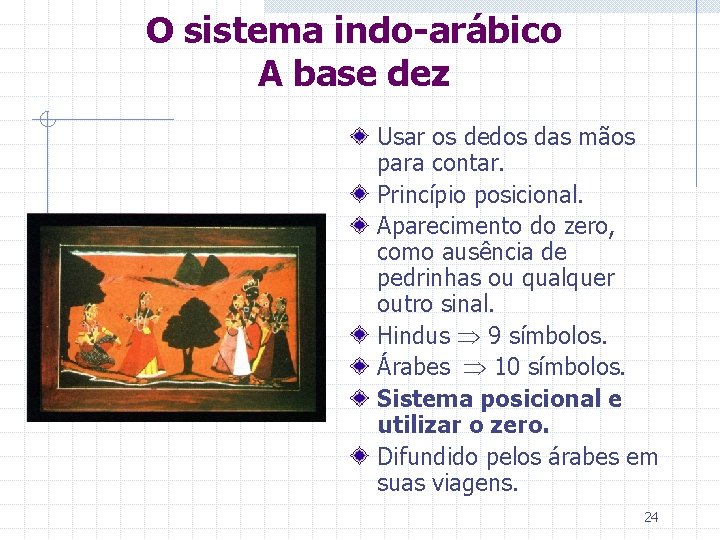
O sistema indo-arábico A base dez Usar os dedos das mãos para contar. Princípio posicional. Aparecimento do zero, como ausência de pedrinhas ou qualquer outro sinal. Hindus 9 símbolos. Árabes 10 símbolos. Sistema posicional e utilizar o zero. Difundido pelos árabes em suas viagens. 24

25

Enfim o zero. . . Revolução nos sistemas de numeração. Sulco das dezenas sem pedrinhas. Hindus Sunya (vazio) Árabe Zefir Português zero Em 876 aparece a mais antiga citação de um zero. Símbolos iniciais um pequeno círculo ou um ponto. Não se sabe qual a primeira civilização a utilizar o zero. 26

Sistema indo-arábico combinação de 3 princípios Tem base dez, ou seja, cada dez unidades de uma ordem forma unidade de ordem imediatamente superior. Utiliza apenas dez símbolos: 0, 1, 2, 3, 4, 5, 6, 7, 8 e 9 com os quais podemos representar qualquer número. Esses símbolos são chamados de algarismos. É um sistema posicional, isto é, um mesmo símbolo representa quantidades diferentes, dependendo da posição em que ele esteja. 27

28

Referências GUELLI, Oscar. A invenção dos números. São Paulo: Ática, 1998. IMENES, Luiz Márcio. Os números na história da civilização. São Paulo: Scipione, 1989. STRUIK, Dirk J. História concisa das matemáticas. Lisboa: Gradiva, 1992. 29