EXPONENTS Laying Down the Laws BASIC VOCABULARY Exponential

EXPONENTS Laying Down the Laws

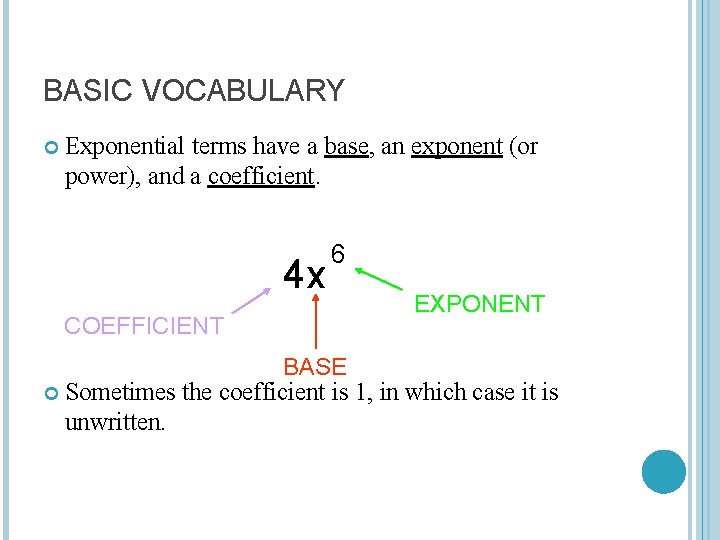
BASIC VOCABULARY Exponential terms have a base, an exponent (or power), and a coefficient. 4 x COEFFICIENT 6 EXPONENT BASE Sometimes the coefficient is 1, in which case it is unwritten.

ADDING TERMS You can ONLY add (or subtract) terms when they have the same base AND the same exponent. 7 a 3 + 3 a 3 In this case, we just add the coefficients. =10 a 3

ADDING TERMS You can ONLY add (or subtract) terms when they have the same base AND the same exponent. This is still true when you have more than one exponent per term. 12 x 7 y 2 – 3 x 7 y 2 =9 x 7 y 2

ADDING TERMS When terms do NOT have the same base AND the same exponent, they cannot be combined. 3 x 4 + 2 x 2 Leave them the way they are.

MULTIPLYING TERMS You can multiply (or divide) terms if they have the same base. The exponents can be different. ∙xx 4 ∙∙xx 3 x 7 This is equivalent to: Which is equal to:

MULTIPLYING TERMS This leads to a rule: To multiply terms with the same base, add the exponents. x 10∙x 5 y 2∙y 7 a 100∙a 50

MULTIPLYING TERMS When terms do NOT have the same base, they cannot be multiplied. x 4 ∙ y 2 Leave them the way they are.

MULTIPLYING TERMS If your term has more than one variable (or a coefficient), treat each piece separately. Remember, multiplication is commutative and associative! (2∙x 2 x 4∙yy 7) (∙ 3 3 x 9 yy) 6 x 13 y 8 This is equivalent to: Which is equal to:

DIVIDING TERMS Since dividing is the inverse of multiplying, what do you do with the exponents? x 4 x 3 This is equivalent to: We cancel out terms that are on top and bottom.

DIVIDING TERMS When dividing terms with the same base, we subtract the exponents!

EXPONENTS OF EXPONENTS For an exponent raised to a power: 3 4 (x ) (x 12) We multiply the exponents! This is equivalent to: Which is equal to:

EXPONENTS OF EXPONENTS You can distribute an exponent across multiplication or division:

EXPONENTS OF EXPONENTS You can NOT, NO WAY, NOT EVER distribute an exponent across addition or subtraction: You have to multiply it out! We’ll be learning a quick way to do this later on.

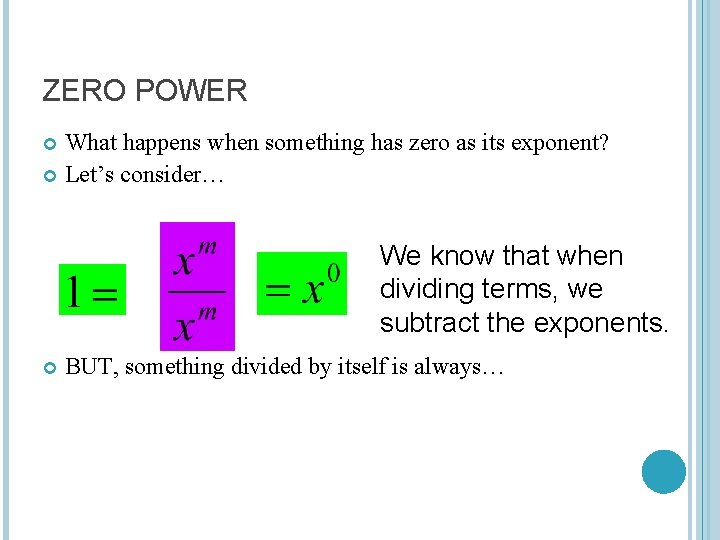
ZERO POWER What happens when something has zero as its exponent? Let’s consider… We know that when dividing terms, we subtract the exponents. BUT, something divided by itself is always…

ZERO POWER So, something with an exponent of zero always equals one.

NEGATIVE EXPONENTS Observe the following pattern: 25 = 32 24 = 16 23 = 8 22 = 4 What is happening?

NEGATIVE EXPONENTS Let’s continue the pattern: Notice…

NEGATIVE EXPONENTS This leads to a rule: A negative exponent drops the base and power to the denominator. Or, if the negative exponent is in the denominator, it raises the base up.

NEGATIVE EXPONENTS

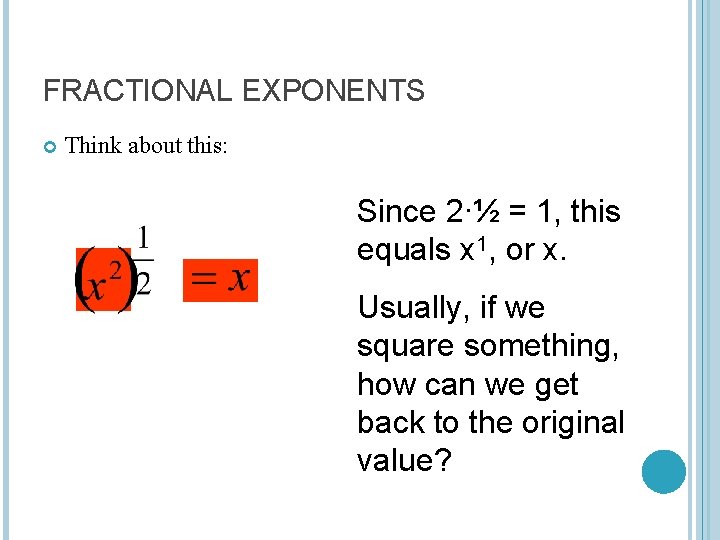
FRACTIONAL EXPONENTS Think about this: Since 2∙½ = 1, this equals x 1, or x. Usually, if we square something, how can we get back to the original value?

FRACTIONAL EXPONENTS A fractional exponent is the same as a root. x 1 5 =

FRACTIONAL EXPONENTS A fractional exponent is the same as a root. x a b = A number in the numerator remains a power.

FRACTIONAL EXPONENTS So,

FRACTIONAL EXPONENTS Simplify:

FRACTIONAL EXPONENTS