EXPONENTS INDEX NOTATION SCIENTIFIC NOTATION Student Notes Index

EXPONENTS (INDEX NOTATION) & SCIENTIFIC NOTATION Student Notes

Index notation We use index notation to show repeated multiplication by the same number. For example, we can use index notation to write 2 × 2 × 2 as 25 index or power base This number is read as ‘two to the power of five’. 25 = 2× 2× 2= 32

Index notation Evaluate the following: 62 = 6× 6= 34 = 3× 3× 3× 3= (– 5)3 = 27 = When we raise a negative number to an odd power the answer is negative. 36 81 – 5 × – 5 = – 125 2× 2× 2× 2= (– 1)5 = – 1 × – 1 = (– 4)4 = – 4 × – 4 = When we raise a negative number to an even power the answer is positive. 128 – 1 64

Calculating powers We can use the xy key on a calculator to find powers. For example, to calculate the value of 74 we key in: 7 xy 4 The calculator shows this as 2401. 74 = 7 × 7 × 7 = 2401 =

The first index law When we multiply two numbers written in index form and with the same base we can see an interesting result. For example, 34 × 32 = (3 × 3 × 3) × (3 × 3) =3× 3× 3× 3 = 36 73 × 75 = = 3(4 + 2) (7 × 7) × (7 × 7 × 7) =7× 7× 7 = 78 = 7(3 + 5) When we multiply two numbers What do you withnotice? the same base the indices are added.

The second index law When we divide two numbers written in index form and with the same base we can see another interesting result. For example, 45 ÷ 42 = 56 ÷ 54 = 4× 4× 4 5× 5× 5× 5 = 4× 4× 4= = 5× 5= 43 = 4(5 – 2) 52 = 5(6 – 4) When we divide two numbers What dowith you the notice? same base the indices are subtracted.

Zero indices Look at the following division: 64 ÷ 64 = 1 Using the second index law, 64 ÷ 64 = 6(4 – 4) = 60 That means that, 60 = 1 In fact, any number raised to the power of 0 is equal to 1. For example, 100 = 1 3. 4520 = 1 723 538 5920 = 1

Negative indices Look at the following division: 32 ÷ 34 3× 3 = = 3× 3× 3× 3 1 3× 3 = 1 32 Using the second index law, 32 ÷ 34 = 3(2 – 4) = 3– 2 That means that, 1 3– 2 = Similarly, 6– 1 = 1 6 7– 4 = 32 1 74 and 5– 3 = 1 53

Negative indices Look at the following division: 32 ÷ 34 3× 3 = 1 = 3× 3× 3× 3 = 1 32 Using the second index law, 32 ÷ 34 = 3(2 – 4) = That means that Similarly, 3– 2 = 6– 1 = 1 6 7– 4 = 3– 2 1 32 1 74 and 5– 3 = 1 53

Index laws for negative indices Here is a summery of the index laws for negative indices. x– 1 = 1 x The reciprocal of x is x–n = 1 n x The reciprocal of xn is 1 xn

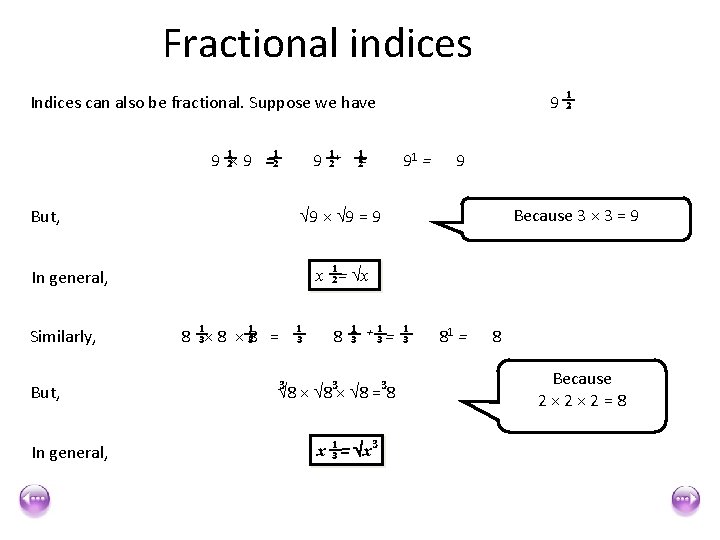
Fractional indices 1 Indices can also be fractional. Suppose we have 1 1 9 2× 9 =2 9 In general, 91 = 9 Because 3 × 3 = 9 x 12= x In general, But, 1 =2 9 × 9 = 9 But, Similarly, 1+ 2 9 2. 1 1 1 3 8 3× 8 × 38 = 3 8 +1 + 1 = 1 3 3 8 × 8 = 8 x 13 = x 3 3 81 = 8 Because 2× 2× 2=8

Index laws for fractional indices Here is a summery of the index laws for fractional indices. x = x 1 2 n x = x 1 n m n n n x = xm or ( x)m

Powers of ten Our decimal number system is based on powers of ten. We can write powers of ten using index notation. 10 = 101 100 = 10 × 10 = 102 1000 = 10 × 10 = 103 10 000 = 10 × 10 = 104 100 000 = 10 × 10 = 105 1 000 = 10 × 10 × 10 = 106 …

Negative powers of ten Any number raised to the power of 0 is 1, so 1 = 100 Decimals can be written using negative powers of ten 0. 1 = =1 =10 -11 1 10 10 0. 01 = =1 100 0. 001 = 0. 00001 = 0. 000001 = = 10 -21 2 10 = 10 -31 3 1000 10 = 10 -4 1 4 10000 10 = 10 -5 1 5 100000 10 = 10 -6 … 1 6 1000000 10

Standard form 2 × 1015 and 1. 5 × 10 -12 are examples of a number written in standard form. Numbers written in standard form have two parts: A number between 1 and 10 × A power of 10 This way of writing a number is also called standard index form or scientific notation. Any number can be written using standard form, however it is usually used to write very large or very small numbers.

Standard form – writing large numbers For example, the mass of the planet earth is about 5 970 000 000 kg. We can write this in standard form as a number between 1 and 10 multiplied by a power of 10. 5. 97 × 1024 kg A number between 1 and 10 A power of ten DO NOT COUNT JUST THE NUMBER OF ZEROS, BUT COUNT THE NUMBER OF TIMES THAT YOU MOVE THE DECIMAL PLACE. BIG NUMBER GET POSITIVE EXPONENTS.

Standard form – writing small numbers We can write very small numbers using negative powers of ten. For example, the width of this shelled amoeba is 0. 00013 m. We write this in standard form as: 1. 3 × 10 -4 m. A power of ten A number between 1 DO NOT COUNT JUST THE NUMBER OF and 10 ZEROS, BUT COUNT THE NUMBER OF TIMES THAT YOU MOVE THE DECIMAL PLACE. BIG NUMBER GET POSITIVE EXPONENTS.

Standard form – writing large numbers How can we write these numbers in standard form? 80 000 = 8 × 107 230 000 = 2. 3 × 108 724 000 = 6 003 000 = 371. 45 = 7. 24 × 105 6. 003 × 109 3. 7145 × 102

Standard form – writing large numbers These numbers are written in standard form. How can they be written as ordinary numbers? 5 × 1010 = 50 000 000 7. 1 × 106 = 7 100 000 4. 208 × 1011 = 420 800 000 2. 168 × 107 = 21 680 000 6. 7645 × 103 = 6764. 5

Standard form – writing small numbers How can we write these numbers in standard form? 0. 0006 = 0. 00000072 = 0. 0000502 = 0. 0000000329 = 0. 001008 = 6 × 10 -4 7. 2 × 10 -7 5. 02 × 10 -5 3. 29 × 10 -8 1. 008 × 10 -3

Standard form – writing small numbers These numbers are written in standard form. How can they be written as ordinary numbers? 8 × 10 -4 = 0. 0008 2. 6 × 10 -6 = 0. 0000026 9. 108 × 10 -8 = 0. 00000009108 7. 329 × 10 -5 = 0. 00007329 8. 4542 × 10 -2 = 0. 084542