Exponents 6 Base Exponent 6 is read Six

Exponents

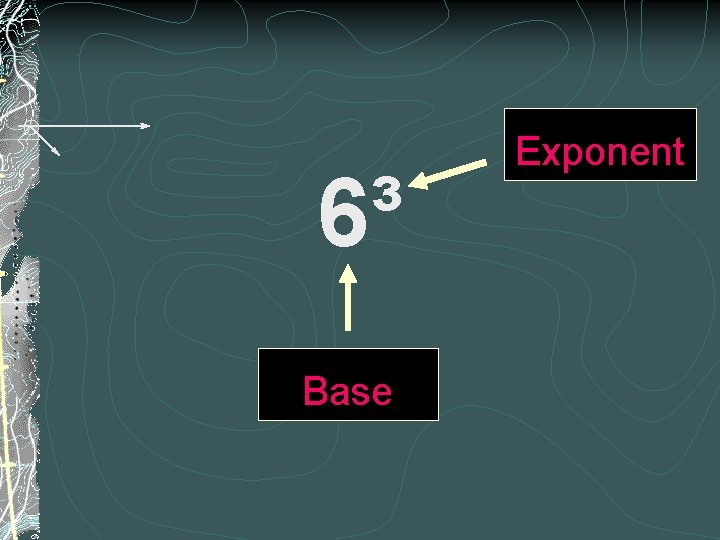
6³ Base Exponent

6³ is read “Six Cubed” 6³ means 6 x 6 x 6 (repeated multiplication) 6³ = 216

§ Any base to the zero power, equals one. Example: 20 = 1 50 1 = § Any base to the first power, equals itself. Example: 41 = 4 71 = 7

Evaluate Exponents § Evaluating Exponents: means to find the VALUE of. 9 Example: 3² = -1 § -9º = -27 §

= Tricky Integer Bases § Exponents tell you how many times to multiply the base Positive Base Negative Base Evaluate: -9 ** Now check your answer with your calculators ** 9

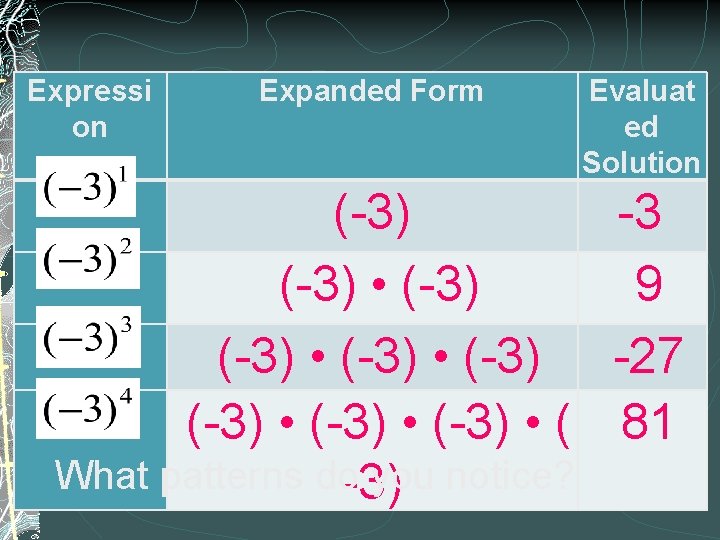
Expressi on Expanded Form Evaluat ed Solution (-3) -3 (-3) • (-3) 9 (-3) • (-3) -27 (-3) • ( 81 What patterns do-3) you notice?

§ If you have a negative base and an odd exponent , the answer is negative. (-5)1 = -5 Example: (-5)3 Example: § If = -125 you have a negative base and an even exponent , the answer 2 = (-5) 25 is positive. (-5)4 = 625

1 3 1 625 16 -1 -7 1 125 -9 100 1 -1

Properties of Exponents Complete the table in your notes and look for a pattern

Rule 1: When multiplying two numbers with the same base, keep base and add the exponents. 3³ x 3². 3 x 3 x 3 3 3 x 3 x 3

Properties of Exponents Complete the table in your notes and look for a pattern

Rule 2: When dividing two numbers with the same base, keep base and subtract the Why exponents. 0 does x = 1?

Rule 3 When raising a number with an exponent to a power, multiply the exponents. (3²)³ (3²) x (3²) 3) (3 x 3) x (3 x

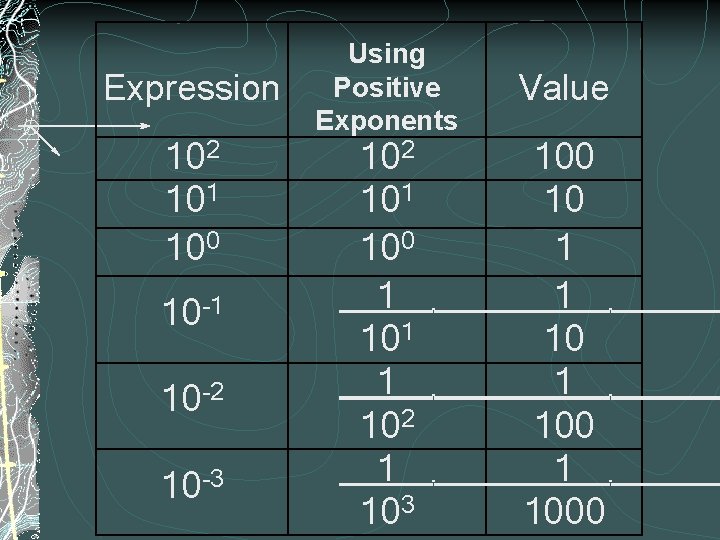
Expression 102 101 100 10 -1 10 -2 10 -3 Using Positive Exponents 102 101 100 1 101 1 102 1 103 . . . Value 100 10 1 1000 . . .

Negative Exponents § Negative Exponents are NOT negative numbers § Negative Exponents are greater than 0, but less than one § Negative Exponents can be written as fractions and decimals

Example = = Negative Exponents Video

Simplify