Exponential Growth Decay Graphs I Exponential Functions A

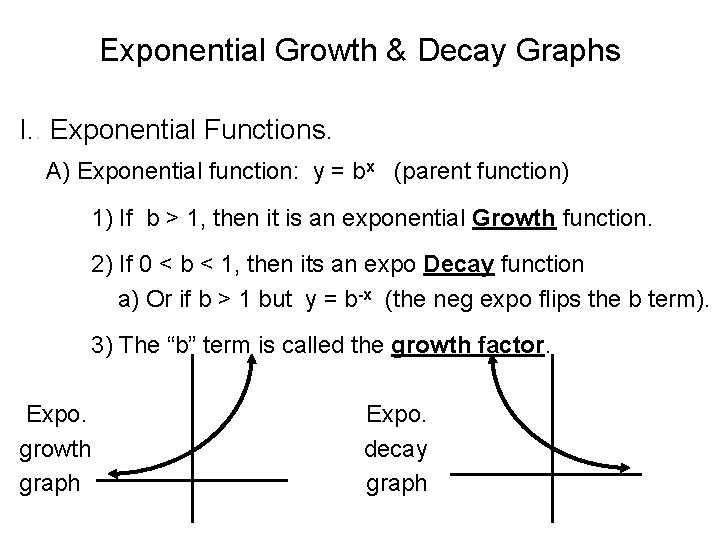
Exponential Growth & Decay Graphs I. . Exponential Functions. A) Exponential function: y = bx (parent function) 1) If b > 1, then it is an exponential Growth function. 2) If 0 < b < 1, then its an expo Decay function a) Or if b > 1 but y = b-x (the neg expo flips the b term). 3) The “b” term is called the growth factor. Expo. growth graph Expo. decay graph

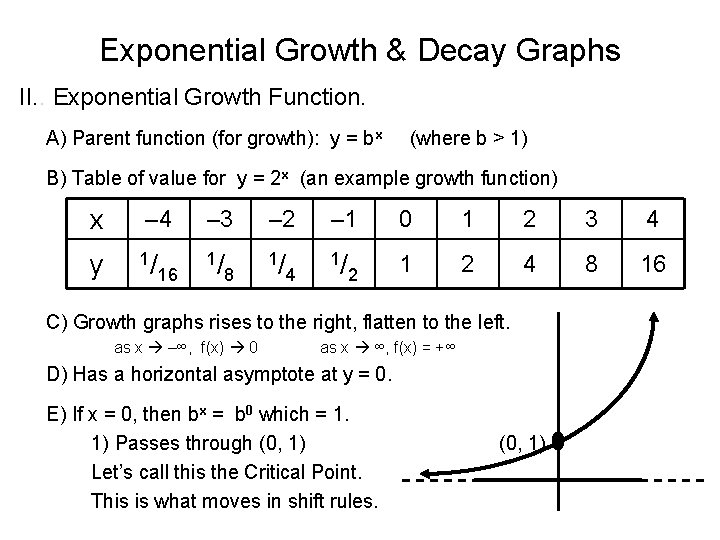
Exponential Growth & Decay Graphs II. . Exponential Growth Function. A) Parent function (for growth): y = bx (where b > 1) B) Table of value for y = 2 x (an example growth function) x y – 4 1/ 16 – 3 – 2 – 1 0 1 2 3 4 1/ 1/ 1/ 1 2 4 8 16 8 4 2 C) Growth graphs rises to the right, flatten to the left. as x –∞, f(x) 0 as x ∞, f(x) = +∞ D) Has a horizontal asymptote at y = 0. E) If x = 0, then bx = b 0 which = 1. 1) Passes through (0, 1) Let’s call this the Critical Point. This is what moves in shift rules. (0, 1)

Exponential Growth & Decay Graphs I. . Exponential Decay Function. A) Parent decay function: y = bx (where 0 < b < 1) 1) Or if b >1 but y = b-x B) The “b” term is called the Decay Factor. C) Decay graph: rises to the left, flattens to the right. as x –∞, f(x) +∞ as x +∞, f(x) = 0 D) Has a horizontal asymptote at y = 0. E) If x = 0, then b 0 = 1 1) Passes thru ( 0 , 1 ) = the critical point. (0 , 1)

Exponential Growth & Decay Graphs III. . Shifts of Exponential Graphs. A) y = bx + d 1) Moves the graph up/down. + is up, – is down. 2) It also moves the horizontal asymptote up/down: y = d. B) y = bx+c (the exponent is a grouping symbol) 1) Moves the graph left/right. + goes , – goes 2) Set the exponent = 0, solve for x for sideways shift. C) y = a • bx (the “a” term is the “slope”) 1) If a > 1, then the graph gets “taller” [vert. stretch]. 2) If 0 < a < 1, then the graph gets “less tall” [vert. shrink]. 3) If a is negative, the graph flips (over the x-axis).

Exponential Growth & Decay Graphs IV. . Sketching Shifted Exponential Functions. y = a • bx+c + d A) State all the shifts. B) Find the new critical point. 1) New critical pt = (sideways shift , add first + last terms) or (–c , a+d) 2) If y = bx+c + d, then the “a” term is 1. (understood 1 • bx+c + d) C) Move the horizontal asymptote (y = d) and draw it. D) Look at the “slope” (the “a” term). 1) Stretched graphs have a crit pt far from the horiz asy. 2) Shrunk graphs have a crit pt close to horiz asy. 3) Flip graphs are below the horizontal asymptote line (they flip).

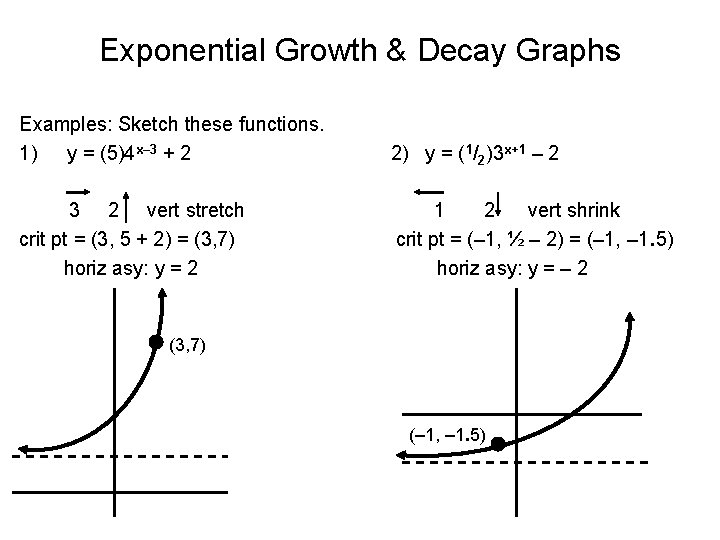
Exponential Growth & Decay Graphs Examples: Sketch these functions. 1) y = (5)4 x– 3 + 2 2) y = ( 1/2)3 x+1 – 2 3 2 vert stretch crit pt = (3, 5 + 2) = (3, 7) horiz asy: y = 2 1 2 vert shrink crit pt = (– 1, ½ – 2) = (– 1, – 1. 5) horiz asy: y = – 2 (3, 7) (– 1, – 1. 5)

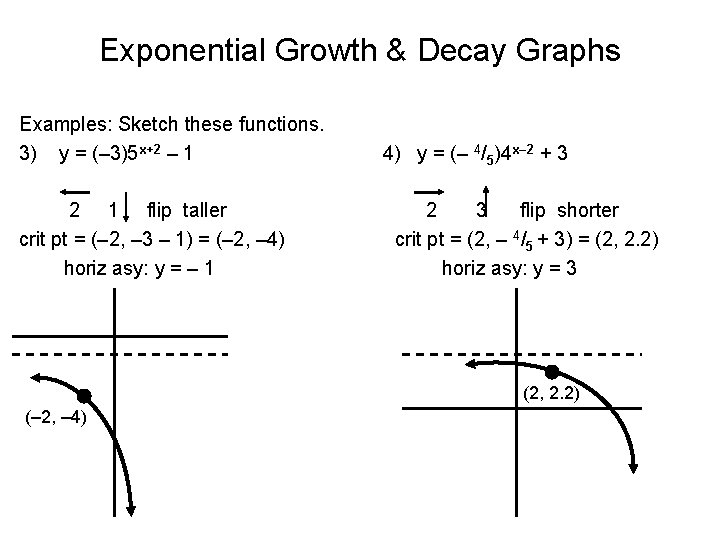
Exponential Growth & Decay Graphs Examples: Sketch these functions. 3) y = (– 3)5 x+2 – 1 2 1 flip taller crit pt = (– 2, – 3 – 1) = (– 2, – 4) horiz asy: y = – 1 4) y = (– 4/5)4 x– 2 + 3 2 3 flip shorter crit pt = (2, – 4/5 + 3) = (2, 2. 2) horiz asy: y = 3 (2, 2. 2) (– 2, – 4)