Exponential Growth and Decay The number of rabbits

Exponential Growth and Decay

The number of rabbits in a population increases at a rate that is proportional to the number of rabbits present (at least for awhile. ) So does any population of living creatures. Other things that increase or decrease at a rate proportional to the amount present include radioactive material and money in an interest-bearing account.

Exponential Change: If the constant k is positive then the equation represents growth. If k is negative then the equation represents decay.

Radioactive Decay The equation for the amount of a radioactive element left after time t is: This allows the decay constant, k, to be positive. The half-life is the time required for half the material to decay.

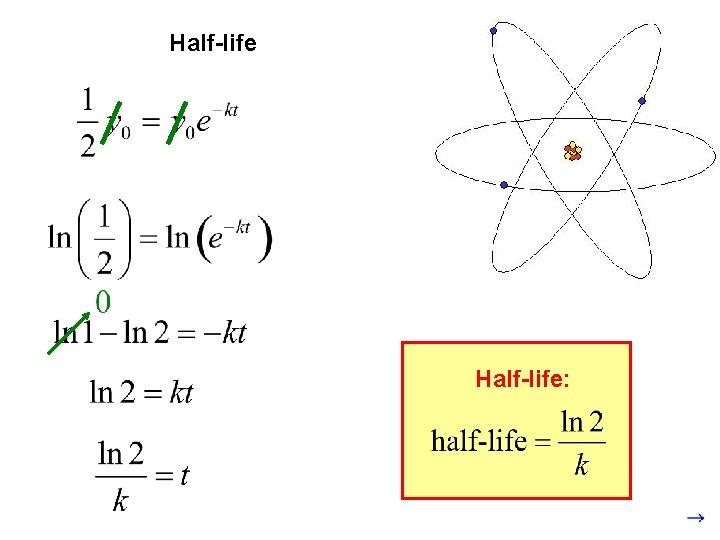
Half-life:

Newton’s Law of Cooling Espresso left in a cup will cool to the temperature of the surrounding air. The rate of cooling is proportional to the difference in temperature between the liquid and the air. (It is assumed that the air temperature is constant. ) If we solve the differential equation: we get: Newton’s Law of Cooling where is the temperature of the surrounding medium, which is a constant, and is the initial temperature. p

Logistics Growth Model

Example: Logistic Growth Model Ten grizzly bears were introduced to a national park 10 years ago. There are 23 bears in the park at the present time. The park can support a maximum of 100 bears. Assuming a logistic growth model, when will the bear population reach 50? 75? 100?

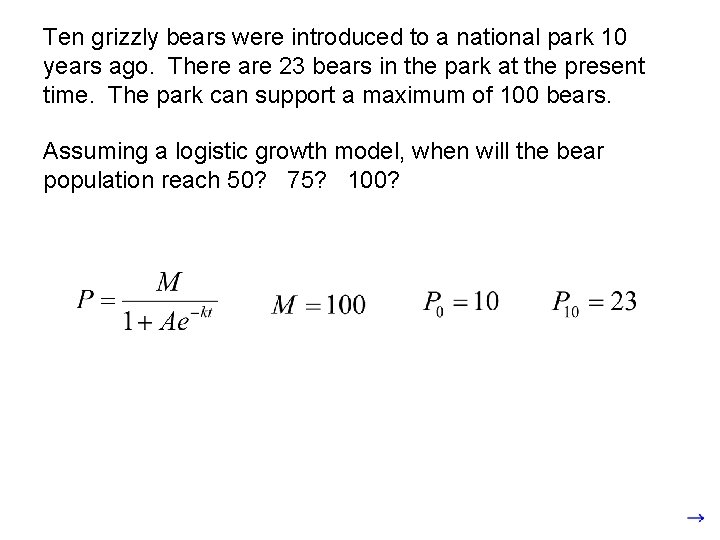
Ten grizzly bears were introduced to a national park 10 years ago. There are 23 bears in the park at the present time. The park can support a maximum of 100 bears. Assuming a logistic growth model, when will the bear population reach 50? 75? 100?

At time zero, the population is 10.

After 10 years, the population is 23.

We can graph this equation and use “trace” to find the solutions. Bears Years y=50 at 22 years y=75 at 33 years y=100 at 75 years

Logistic Growth Model Bears Years