Exponential Growth and Decay ALGEBRA 1 LESSON 6

Exponential Growth and Decay ALGEBRA 1 LESSON 6 -3 (For help, go to Lesson 4 -3. ) Use the formula I = prt to find the interest for principal p, interest rate r, and time t in years. 1. principal: $1000; interest rate: 5%; time: 2 years 2. principal: $360; interest rate: 6%; time: 3 years 3. principal: $2500; interest rate: 4. 5%; time: 2 years 4. principal: $1680; interest rate: 5. 25%; time: 4 years 5. principal: $1350; interest rate: 4. 8%; time: 5 years 6 -3

Exponential Growth and Decay ALGEBRA 1 LESSON 6 -3 Solutions 1. l = prt = ($1000)(0. 05)(2) = $50(2) = $100 2. l = prt = ($360)(0. 06)(3) = $21. 60(3) = $64. 80 3. l = prt = ($2500)(0. 045)(2) = $112. 50(2) = $225 4. l = prt = ($1680)(0. 0525)(4) = $88. 20(4) = $352. 80 5. l = prt = ($1350)(0. 048)(5) = $64. 80(5) = $324 6 -3

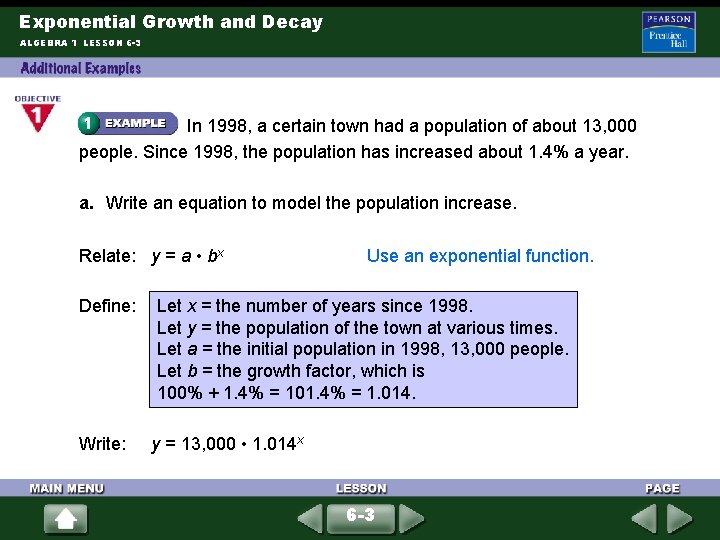
Exponential Growth and Decay ALGEBRA 1 LESSON 6 -3 In 1998, a certain town had a population of about 13, 000 people. Since 1998, the population has increased about 1. 4% a year. a. Write an equation to model the population increase. Relate: y = a • bx Define: Write: Use an exponential function. Let x = the number of years since 1998. Let y = the population of the town at various times. Let a = the initial population in 1998, 13, 000 people. Let b = the growth factor, which is 100% + 1. 4% = 101. 4% = 1. 014. y = 13, 000 • 1. 014 x 6 -3

Exponential Growth and Decay ALGEBRA 1 LESSON 6 -3 (continued) b. Use your equation to find the approximate population in 2006. y = 13, 000 • 1. 014 x y = 13, 000 • 1. 0148 14, 529 2006 is 8 years after 1998, so substitute 8 for x. Use a calculator. Round to the nearest whole number. The approximate population of the town in 2006 is 14, 529 people. 6 -3

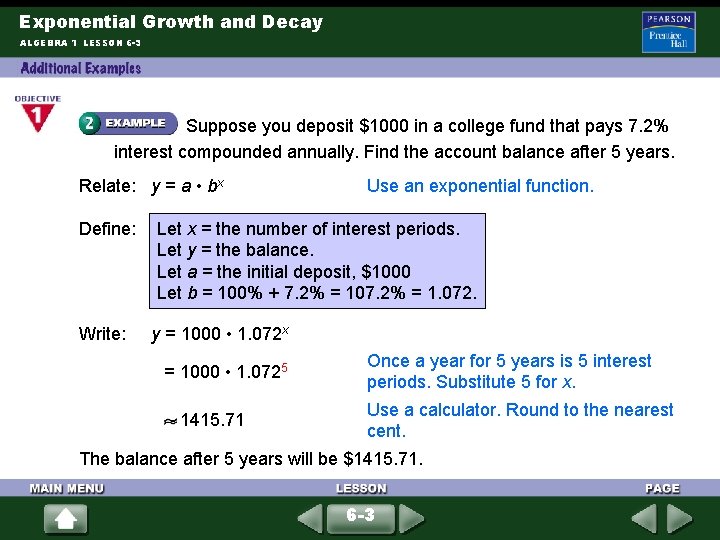
Exponential Growth and Decay ALGEBRA 1 LESSON 6 -3 Suppose you deposit $1000 in a college fund that pays 7. 2% interest compounded annually. Find the account balance after 5 years. Relate: y = a • bx Define: Write: Use an exponential function. Let x = the number of interest periods. Let y = the balance. Let a = the initial deposit, $1000 Let b = 100% + 7. 2% = 107. 2% = 1. 072. y = 1000 • 1. 072 x = 1000 • 1. 0725 1415. 71 Once a year for 5 years is 5 interest periods. Substitute 5 for x. Use a calculator. Round to the nearest cent. The balance after 5 years will be $1415. 71. 6 -3

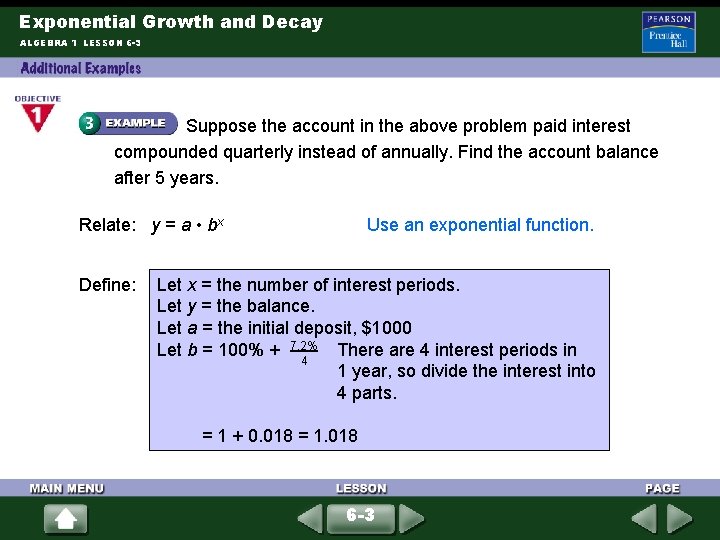
Exponential Growth and Decay ALGEBRA 1 LESSON 6 -3 Suppose the account in the above problem paid interest compounded quarterly instead of annually. Find the account balance after 5 years. Relate: y = a • bx Define: Use an exponential function. Let x = the number of interest periods. Let y = the balance. Let a = the initial deposit, $1000 Let b = 100% + 7. 2% There are 4 interest periods in 4 1 year, so divide the interest into 4 parts. = 1 + 0. 018 = 1. 018 6 -3

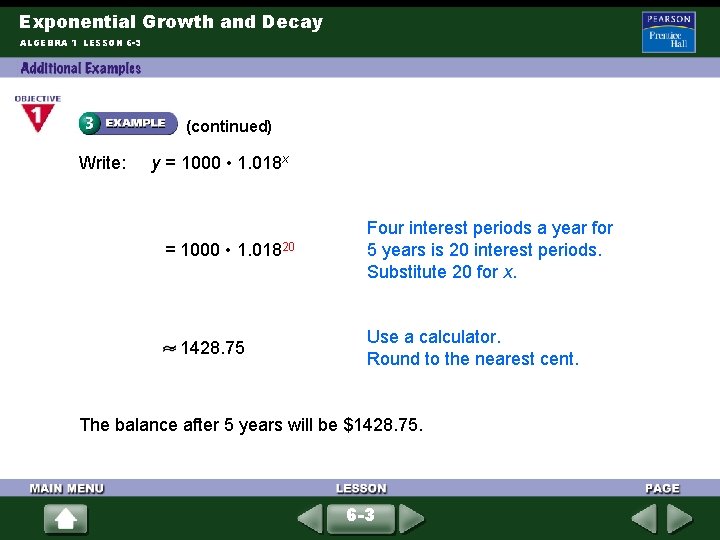
Exponential Growth and Decay ALGEBRA 1 LESSON 6 -3 (continued) Write: y = 1000 • 1. 018 x = 1000 • 1. 01820 1428. 75 Four interest periods a year for 5 years is 20 interest periods. Substitute 20 for x. Use a calculator. Round to the nearest cent. The balance after 5 years will be $1428. 75. 6 -3

Exponential Growth and Decay ALGEBRA 1 LESSON 6 -3 Technetium-99 has a half-life of 6 hours. Suppose a lab has 80 mg of technetium-99. How much technetium-99 is left after 24 hours? In 24 hours there are four 6 -hour half lives. After one half-life, there are 40 mg. After two half-lives, there are 20 mg. After three half-lives, there are 10 mg. After four half-lives, there are 5 mg. 6 -3

Exponential Growth and Decay ALGEBRA 1 LESSON 6 -3 Suppose the population of a certain endangered species has decreased 2. 4% each year. Suppose there were 60 of these animals in a given area in 1999. a. Write an equation to model the number of animals in this species that remain alive in that area. Relate: y = a • bx Define: Write: Use an exponential function. Let x = the number of years since 1999 Let y = the number of animals that remain Let a = 60, the initial population in 1999 Let b = the decay factor, which is 100% - 2. 4 % = 97. 6% = 0. 976 y = 60 • 0. 976 x 6 -3

Exponential Growth and Decay ALGEBRA 1 LESSON 6 -3 (continued) b. Use your equation to find the approximate number of animals remaining in 2005. y = 60 • 0. 976 x y = 60 • 0. 9766 52 2005 is 6 years after 1999, so substitute 6 for x. Use a calculator. Round to the nearest whole number. The approximate number of animals of this endangered species remaining in the area in 2005 is 52. 6 -3

Exponential Growth and Decay ALGEBRA 1 LESSON 6 -3 1. Identify the original amount a and the growth factor b in the exponential function y = 10 • 1. 036 x. a = 10, b = 1. 036 2. A population of 24, 500 people has been increasing at a rate of 1. 8% a year. What will be the population in 15 years if it continues at that rate? about 32, 017 people 3. Write an exponential function to represent $2000 principal earning 5. 6% interest compounded annually. y = 2000 • 1. 056 x 4. Find the account balance on $3000 principal earning 6. 4% interest compounded quarterly for 7 years. about $4678. 91 5. The half-life of a certain substance is 4 days. If you have 100 mg of the substance, how much of it will remain after 12 days? 12. 5 mg 6. The value of a $1200 computer decreases 27% annually. What will be the value of the computer after 3 years? about $466. 82 6 -3