Exponential functions yax What do they look like





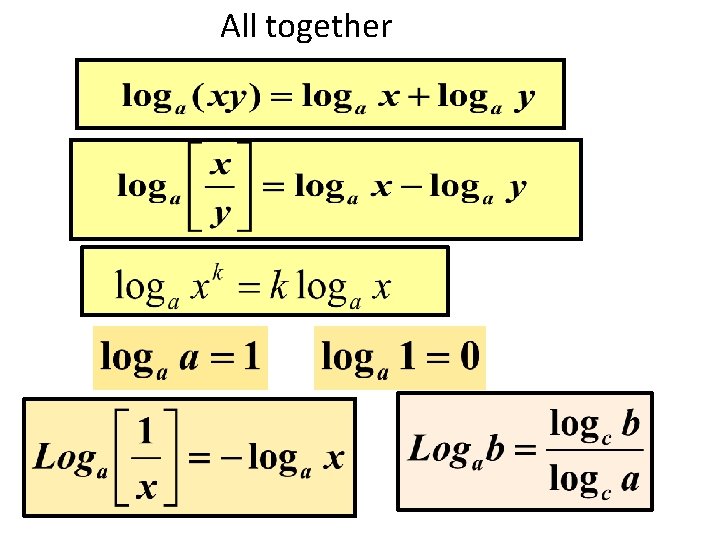

- Slides: 17

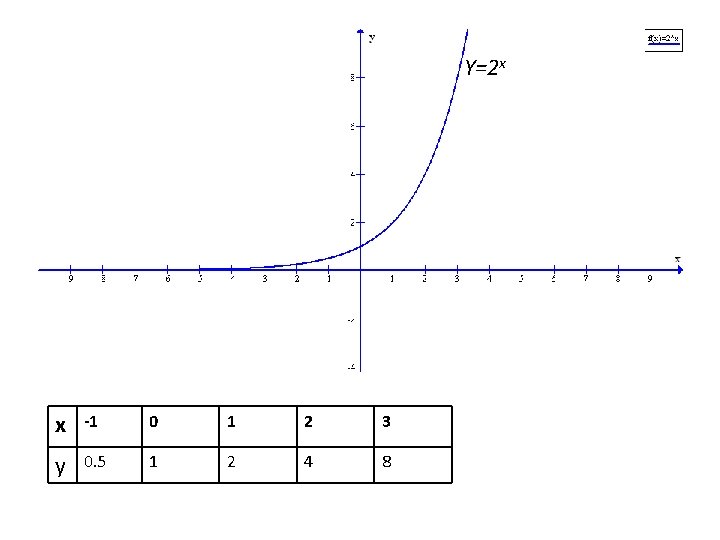
Exponential functions y=ax What do they look like ? y= 2 x looks like this

Y=2 x x -1 0 1 2 3 y 0. 5 1 2 4 8

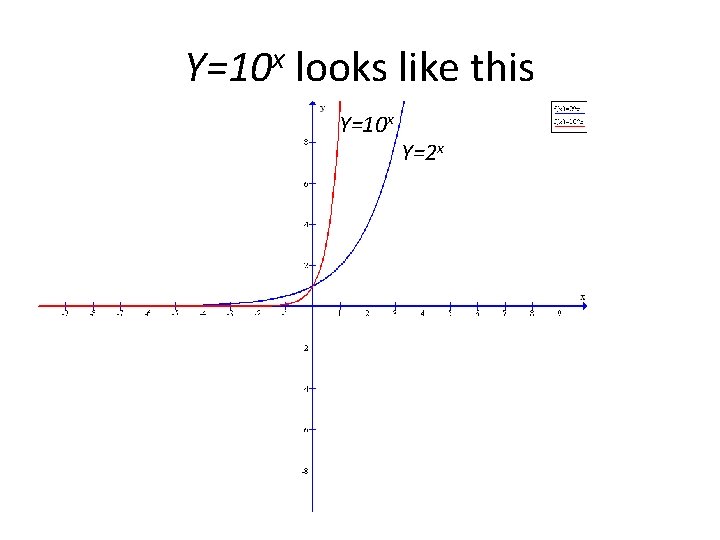
Y=10 x looks like this Y=10 x Y=2 x

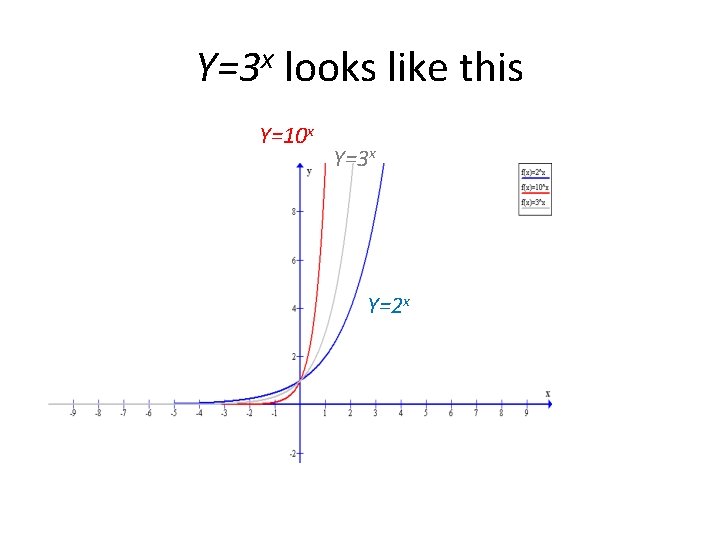
Y=3 x looks like this Y=10 x Y=3 x Y=2 x

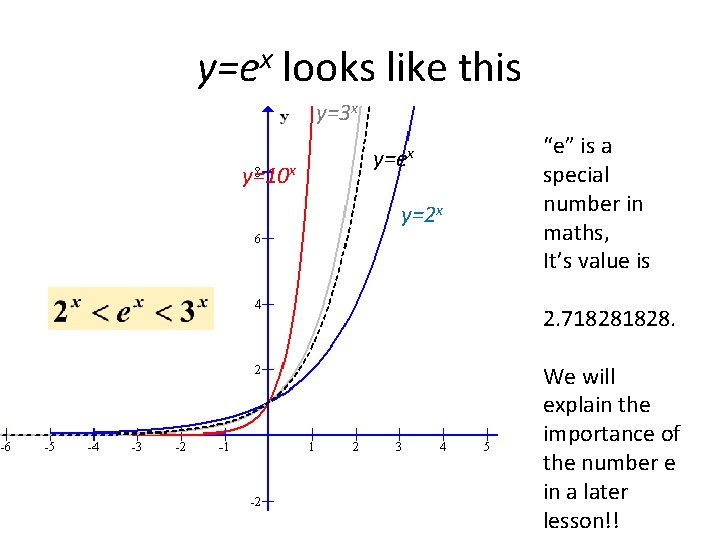
y=ex looks like this y=3 x y=10 x y=ex y=2 x “e” is a special number in maths, It’s value is 2. 71828. We will explain the importance of the number e in a later lesson!!

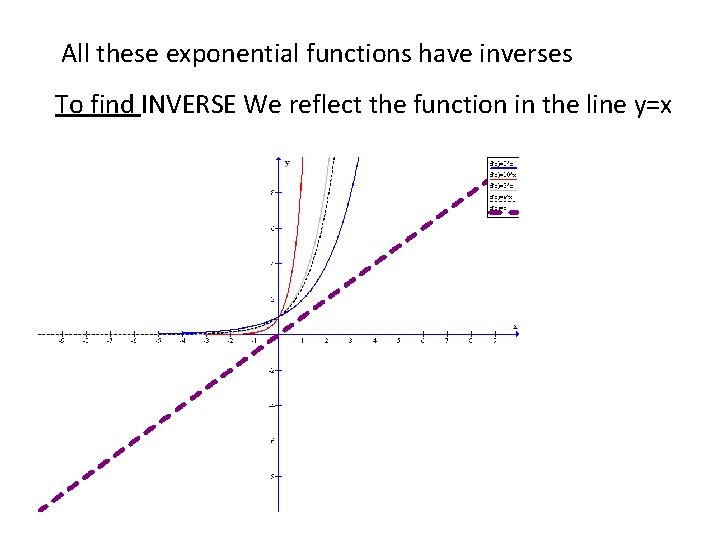
All these exponential functions have inverses To find INVERSE We reflect the function in the line y=x

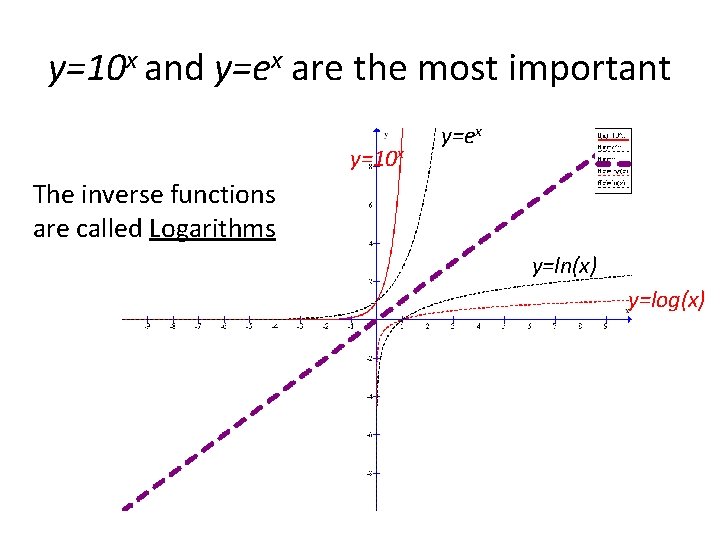
y=10 x and y=ex are the most important y=10 x y=ex The inverse functions are called Logarithms y=ln(x) y=log(x)

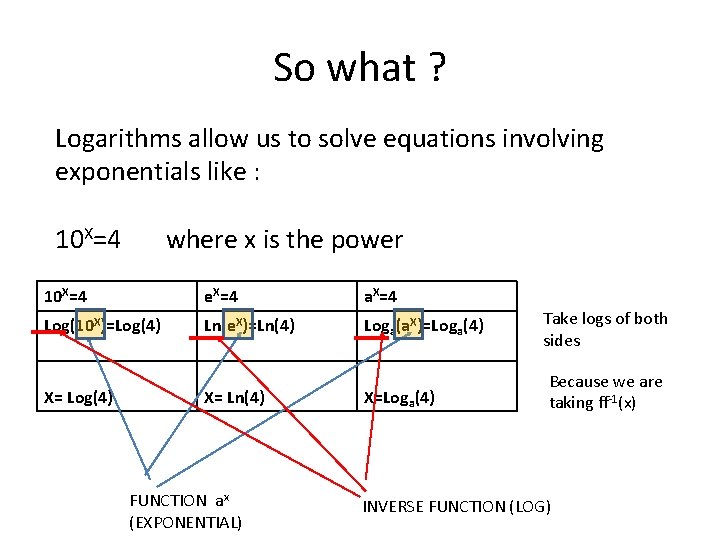
In General for y=ax Function F(x) = 10 x ex ax INVERSE F-1(x) = Log 10(x) Loge(x) Loga(x) a is any constant Remember ff-1(x) = f-1 f(x) = x Log 10(x) is written as simply Log(x) Loge(x) is written as Ln(x) Natural or Naperian Log

So what ? Logarithms allow us to solve equations involving exponentials like : 10 X=4 where x is the power 10 X=4 e. X=4 a. X=4 Log(10 X)=Log(4) Ln(e. X)=Ln(4) Loga(a. X)=Loga(4) X= Log(4) X= Ln(4) FUNCTION ax (EXPONENTIAL) X=Loga(4) Take logs of both sides Because we are taking ff-1(x) INVERSE FUNCTION (LOG)

So if 10 x=4 then x=Log(4) The power “x” is therefore a logarithm !! Logarithms are powers in disguise !! And so the laws of logs are a little like the laws of indices

Log Laws – Rule 1 Indices Log Laws – Rule 2 Indices Logs

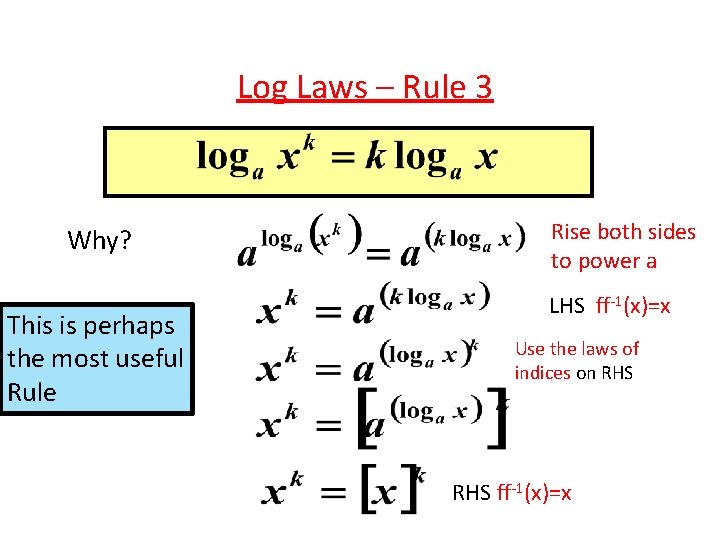
Log Laws – Rule 3 Why? This is perhaps the most useful Rule Rise both sides to power a LHS ff-1(x)=x Use the laws of indices on RHS ff-1(x)=x

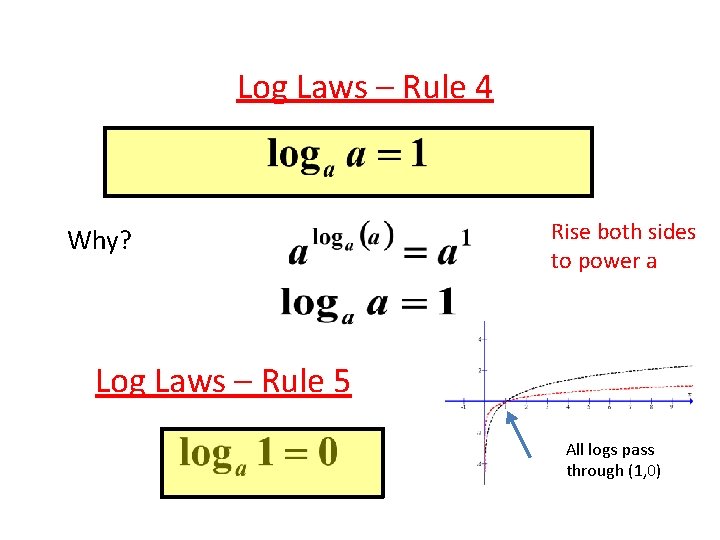
Log Laws – Rule 4 Why? Rise both sides to power a Log Laws – Rule 5 All logs pass through (1, 0)

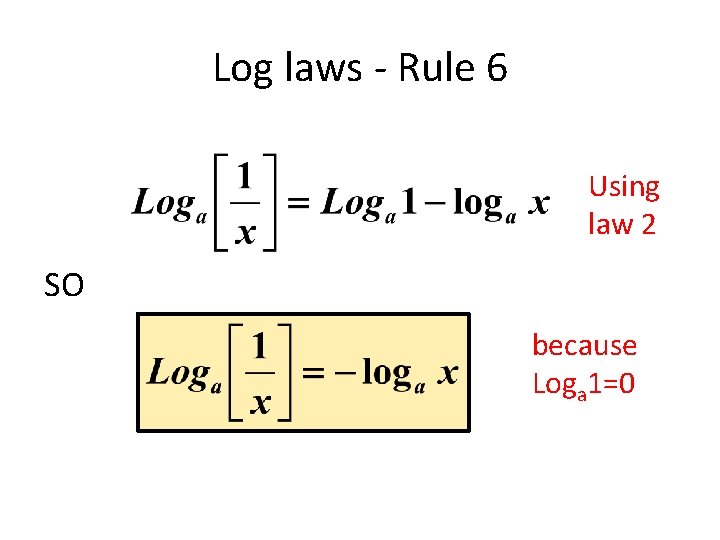
Log laws - Rule 6 Using law 2 SO because Loga 1=0

Log laws - Rule 7 The change of base rule Take Logs of both sides Using Log Law 3 BUT y=logab Why?
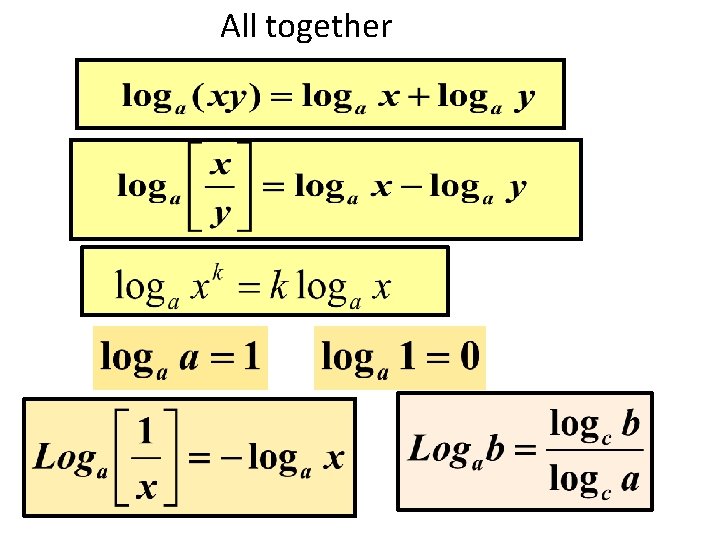
All together

What now 1 - The laws of logarithms are given to you in an exam, you don’t have to remember them 2 - But you do have to use them 3 - We use logarithms to solve things like ax=b 4 - And now you know why!! Because they undo the exponential ax ; as they are it’s Inverse : Next we will use logarithms