Exponential Functions The equation y bx is an

Exponential Functions The equation y = bx is an exponential function provided that b is a positive number other than 1. Exponential functions have variables as exponents. Generalizations about Exponential Functions • The domain is the set of real numbers, and the range is the set of positive real numbers • if b > 1, the graph of y = bx rises from left to right and intersects the y-axis at (0, 1). As x decreases, the negative x-axis is a horizontal asymptote of the graph. • If 0 < b < 1, the graph of y = bx falls from left to right and intersects the y-axis at (0, 1). As x increases, the positive x -axis is a horizontal asymptote of the graph.

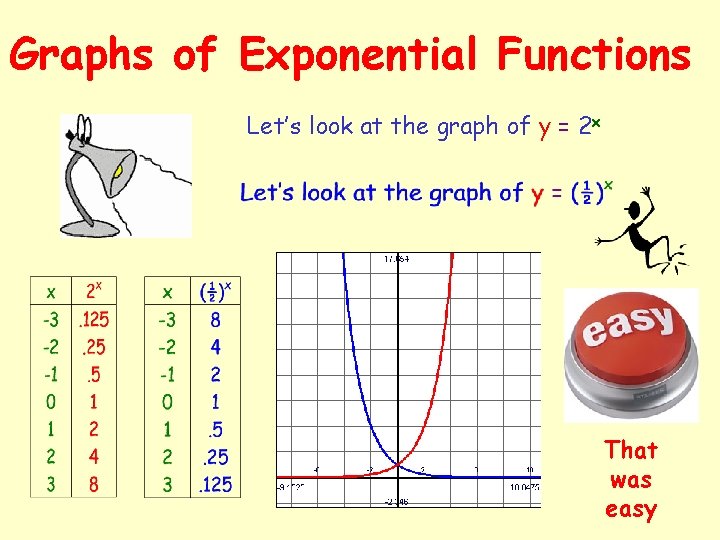
Graphs of Exponential Functions Let’s look at the graph of y = 2 x That was easy

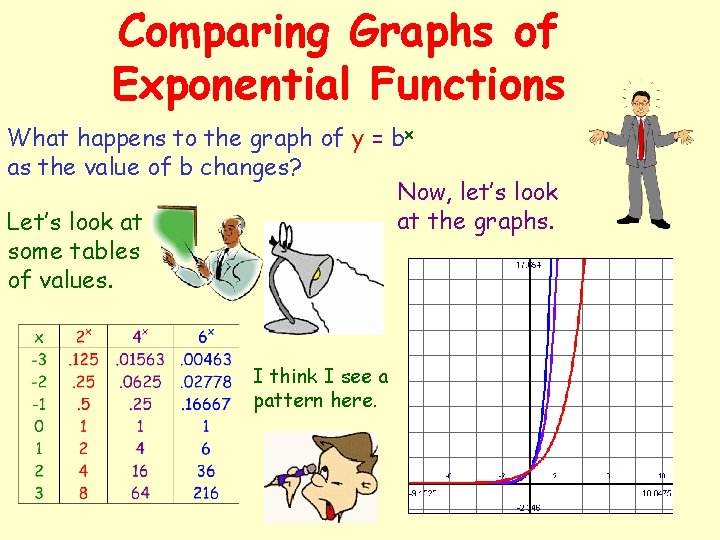
Comparing Graphs of Exponential Functions What happens to the graph of y = bx as the value of b changes? Now, let’s look at the graphs. Let’s look at some tables of values. I think I see a pattern here.

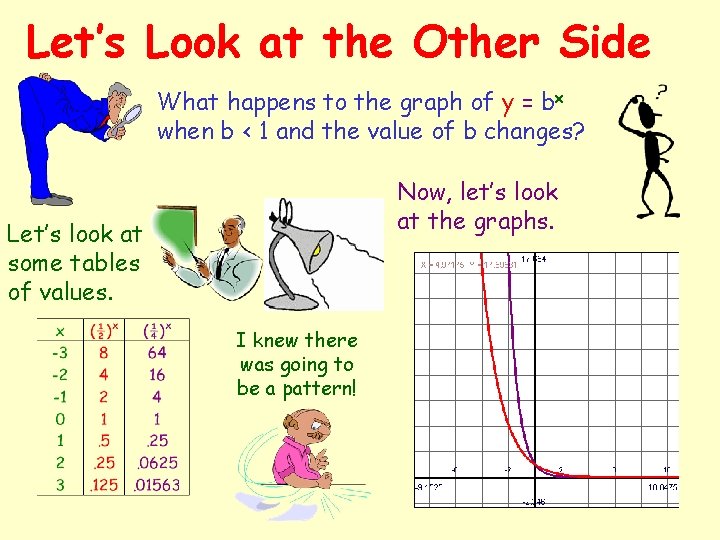
Let’s Look at the Other Side What happens to the graph of y = bx when b < 1 and the value of b changes? Now, let’s look at the graphs. Let’s look at some tables of values. I knew there was going to be a pattern!

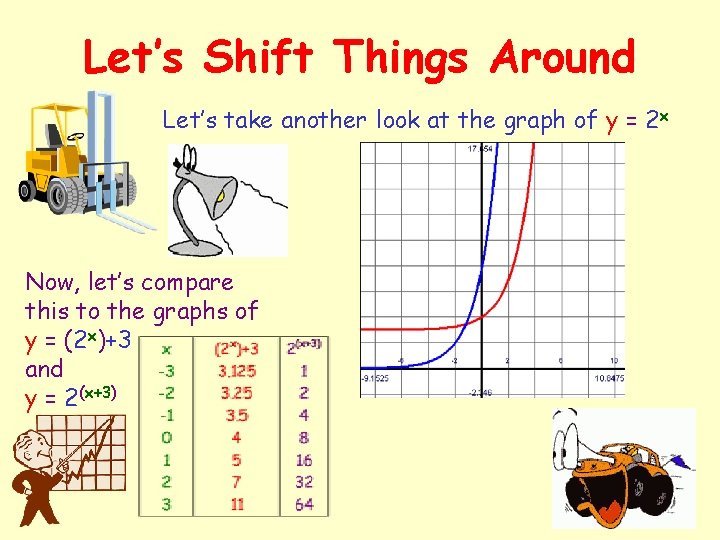
Let’s Shift Things Around Let’s take another look at the graph of y = 2 x Now, let’s compare this to the graphs of y = (2 x)+3 and y = 2(x+3)

Translations of Exponential Functions The translation Th, k maps y = f(x) to y = f(x - h) + k Hey, that rings a bell! It looks like that evaluating functions stuff. Remember if f(x) = x 2, then f(a - 3) = (a - 3)2 Since y and f(x) are the Sam Ting, We can apply this concept to the equation y = bx It’s all starting to come back to me now.

Let’s take a closer look If y = bx and y = f(x), then f(x) = bx This is a little confusing, but I’m sure it gets easier. If the translation Th, k maps y = f(x) to y = f(x - h) + k Then the translation Th, k maps y = bx to y = b(x - h) + k This will be easier to understand if we put some numbers in here.

Now we have a Formula The translation Th, k maps y = bx to y = b(x - h) + k Let’s try a translation on our basic exponential equation Let’s apply the transformation T 3, 1 to the equation y = 2 x The transformed equation would be y = 2(x - 3) + 1 I’m not ready to push the easy button yet. Let’s look at some other examples first.

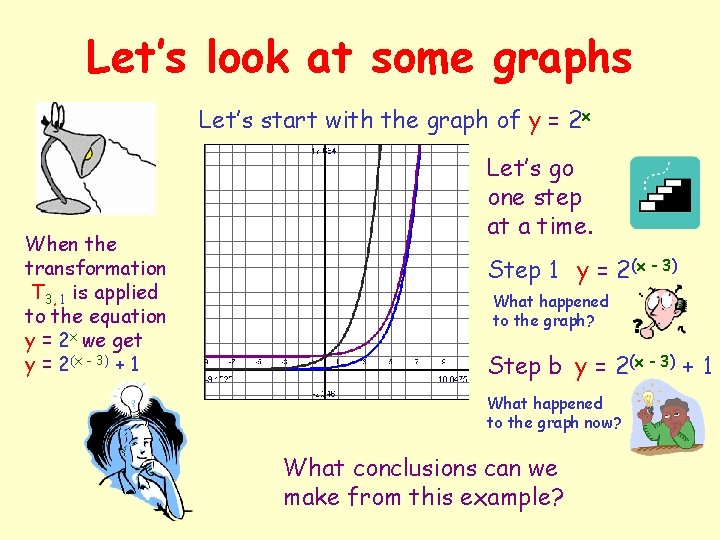
Let’s look at some graphs Let’s start with the graph of y = 2 x When the transformation T 3, 1 is applied to the equation y = 2 x we get y = 2(x - 3) + 1 Let’s go one step at a time. Step 1 y = 2(x - 3) What happened to the graph? Step b y = 2(x - 3) + 1 What happened to the graph now? What conclusions can we make from this example?

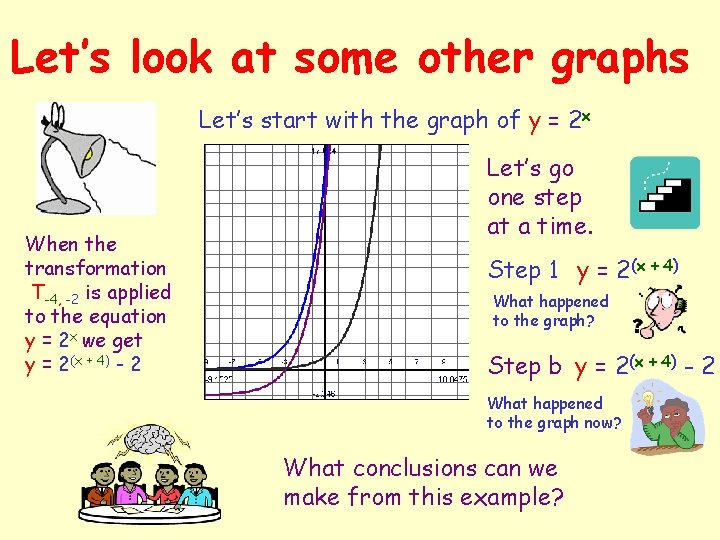
Let’s look at some other graphs Let’s start with the graph of y = 2 x When the transformation T-4, -2 is applied to the equation y = 2 x we get y = 2(x + 4) - 2 Let’s go one step at a time. Step 1 y = 2(x + 4) What happened to the graph? Step b y = 2(x + 4) - 2 What happened to the graph now? What conclusions can we make from this example?

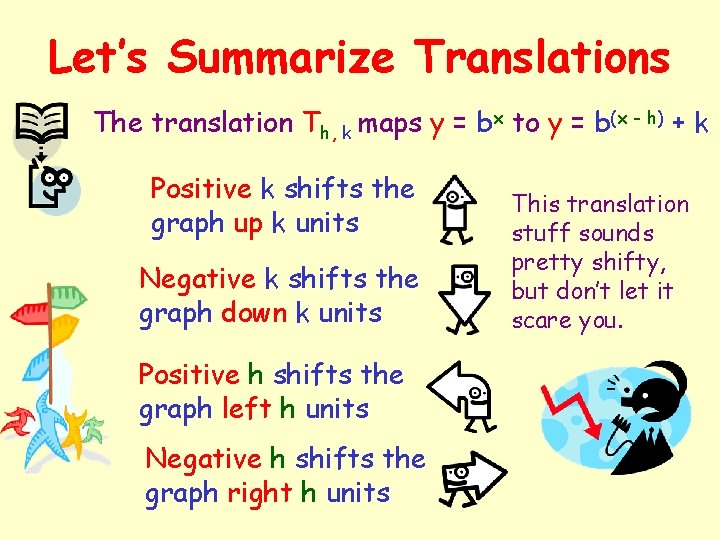
Let’s Summarize Translations The translation Th, k maps y = bx to y = b(x - h) + k Positive k shifts the graph up k units Negative k shifts the graph down k units Positive h shifts the graph left h units Negative h shifts the graph right h units This translation stuff sounds pretty shifty, but don’t let it scare you.

This exponential equation stuff is pretty easy. I feel like jumping for joy! Oh my! I think I’ll just push the easy button. That was easy