Exponential Functions and Their Graphs Base is 2

Exponential Functions and Their Graphs

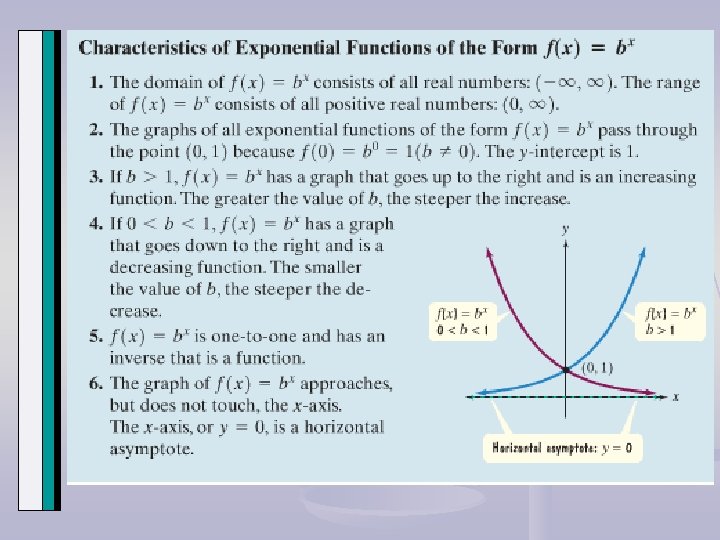
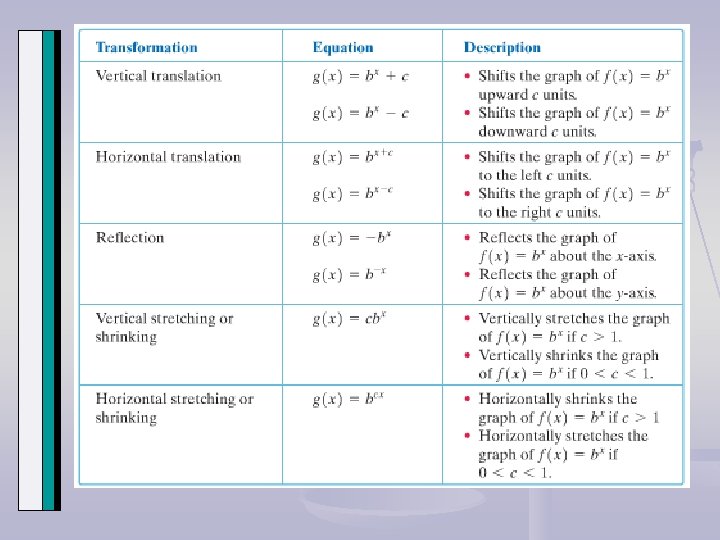
Base is 2 Base is 10 Base is 3 Base is ½ The base is a positive number excluding 1 and the exponent is a variable. The parent form of the graph has a y-intercept at (0, 1). The value of b determines the steepness of the curve.

The following functions are not exponential functions: Variable is the base and not the exponent The base of an exponential function must be a positive number other than 1 The base of an exponential function must be positive Variable is both the base and the exponent
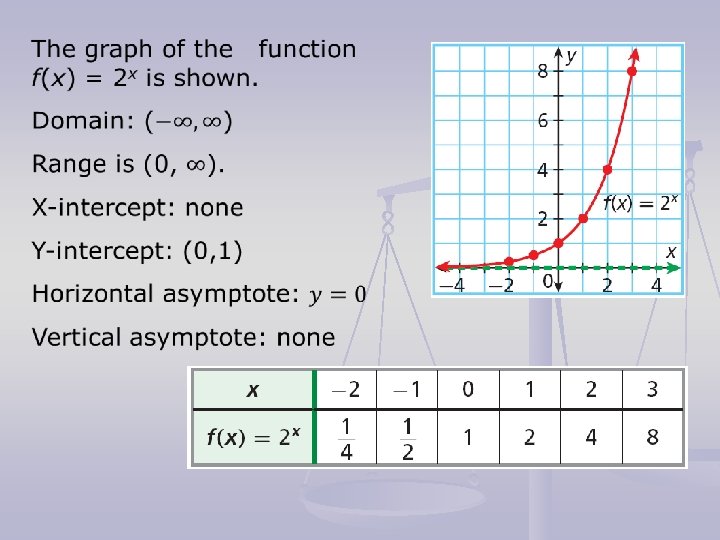
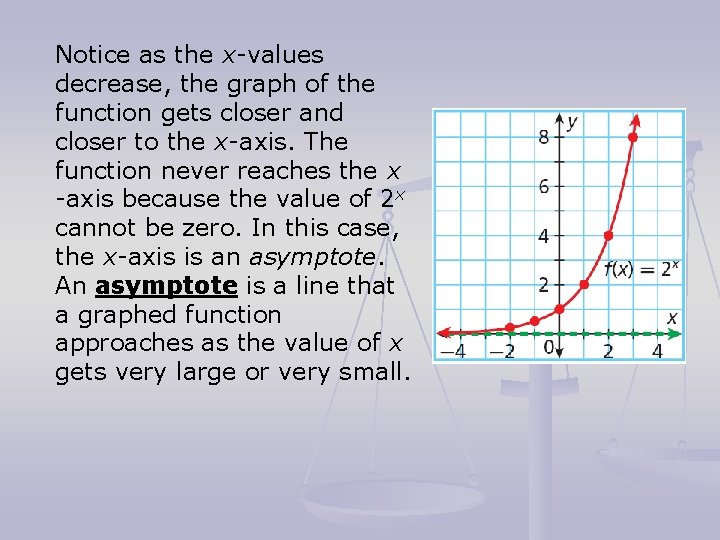
Notice as the x-values decrease, the graph of the function gets closer and closer to the x-axis. The function never reaches the x -axis because the value of 2 x cannot be zero. In this case, the x-axis is an asymptote. An asymptote is a line that a graphed function approaches as the value of x gets very large or very small.
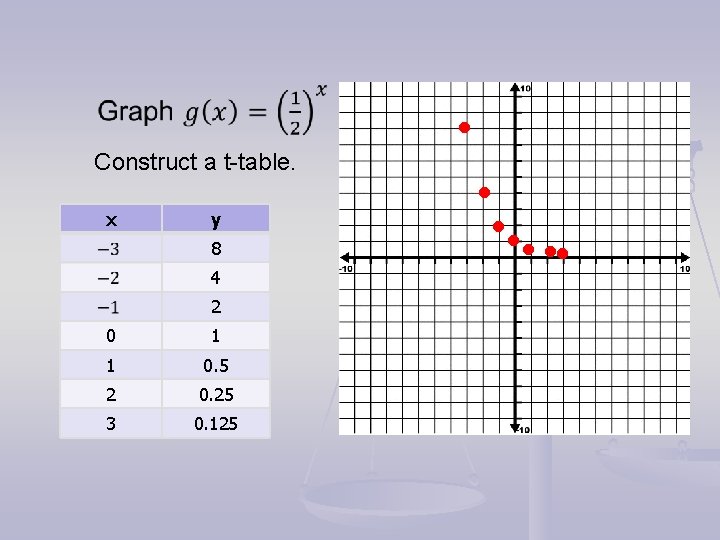
Construct a t-table. x y 8 4 2 0 1 1 0. 5 2 0. 25 3 0. 125
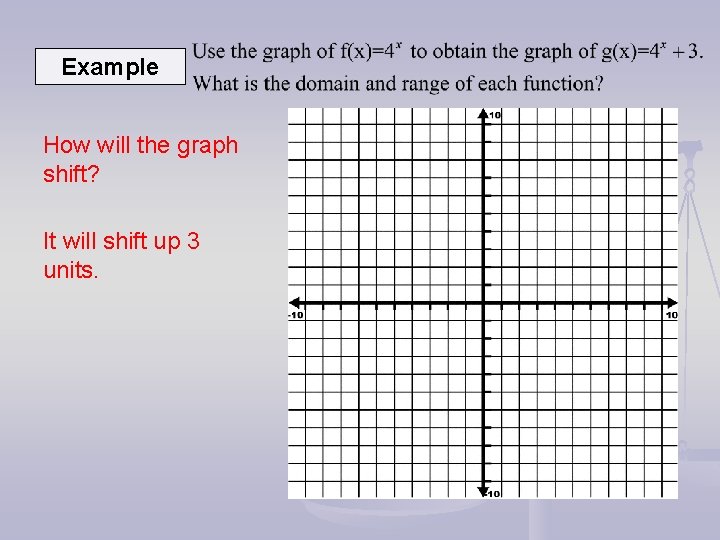
Example How will the graph shift? It will shift up 3 units.
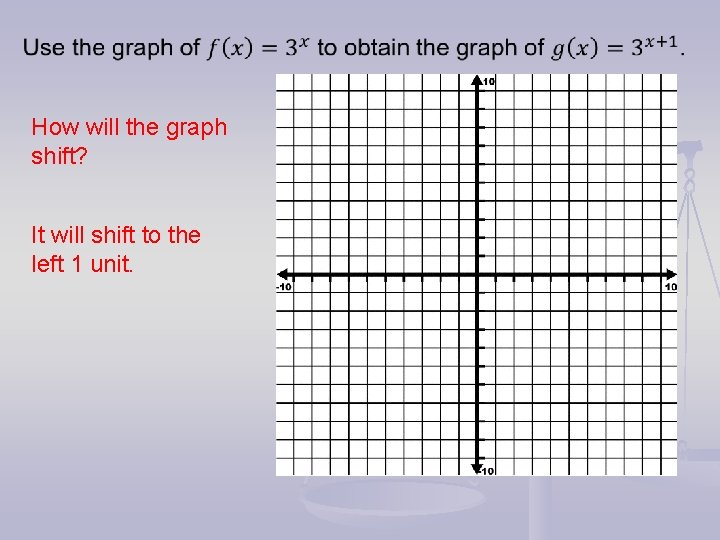
How will the graph shift? It will shift to the left 1 unit.

Example We expect two O-rings to fail at the temperature of 40 degrees.

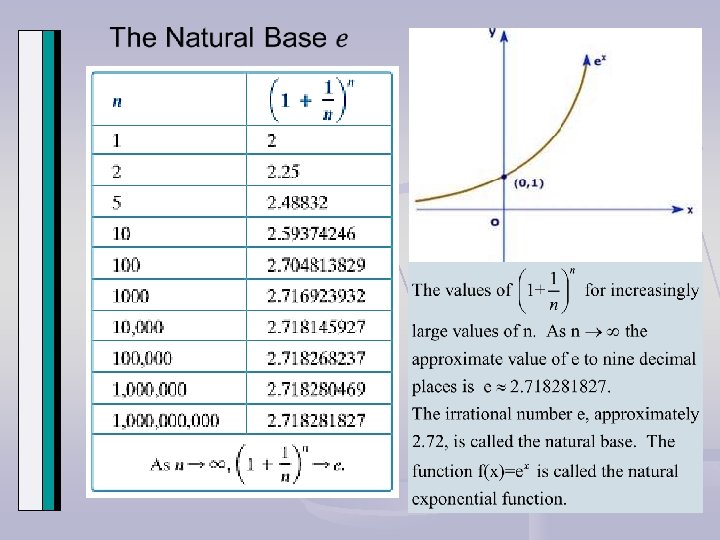
The Natural Base e • The letter e is the initial of the last name of Leonhard Euler (1701 -1783) who introduced the notation. • Since has special calculus properties that simplify many calculations, it is the natural base of exponential functions. • The value of e is defined as the number that the expression approaches as n approaches infinity. • The value of e to 16 decimal places is 2. 718284590452. • The function is called the Natural Exponential Function

Example

- Slides: 15