EXPONENTIAL DISTRIBUTION THE PROBABILITY DENSITY FUNCTION If a

EXPONENTIAL DISTRIBUTION THE PROBABILITY DENSITY FUNCTION • If a random variable X is exponentially distributed with parameter then its probability density function is given by • Mean, = standard deviation, = 1/ • The probability P(X a) is obtained as follows: • If mean, is given, find the parameter first (see Example 2): =1/ 1

EXPONENTIAL DISTRIBUTION Example 1: Let X be an exponential random variable with =2. Find the following: 2

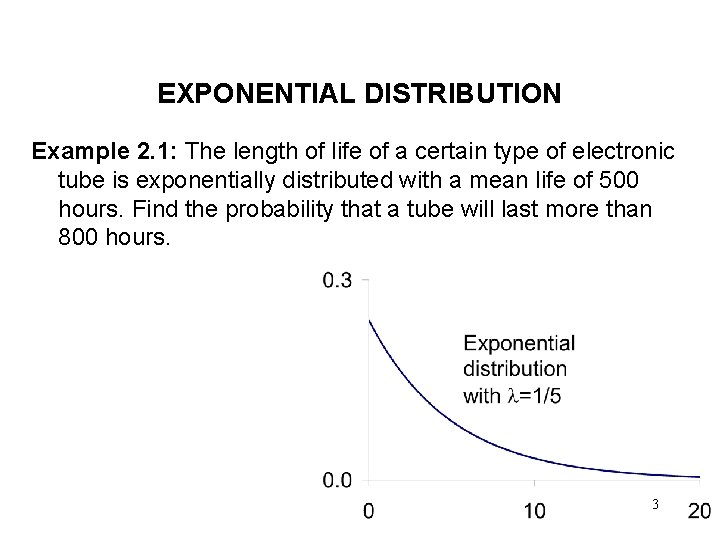
EXPONENTIAL DISTRIBUTION Example 2. 1: The length of life of a certain type of electronic tube is exponentially distributed with a mean life of 500 hours. Find the probability that a tube will last more than 800 hours. 3

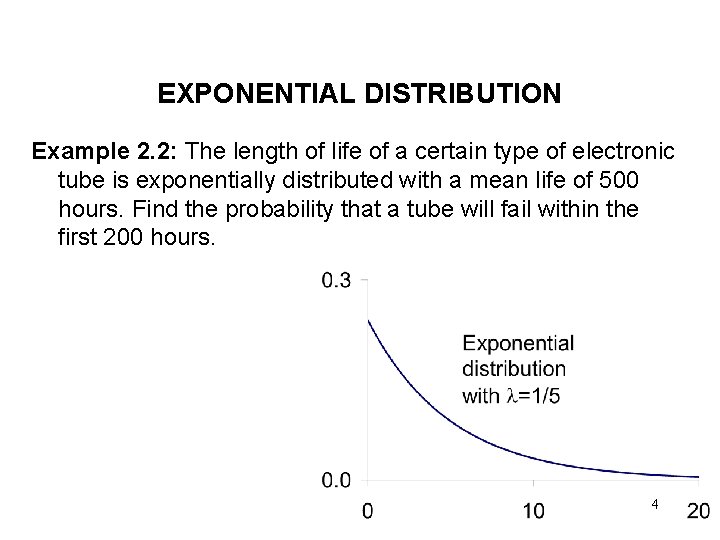
EXPONENTIAL DISTRIBUTION Example 2. 2: The length of life of a certain type of electronic tube is exponentially distributed with a mean life of 500 hours. Find the probability that a tube will fail within the first 200 hours. 4

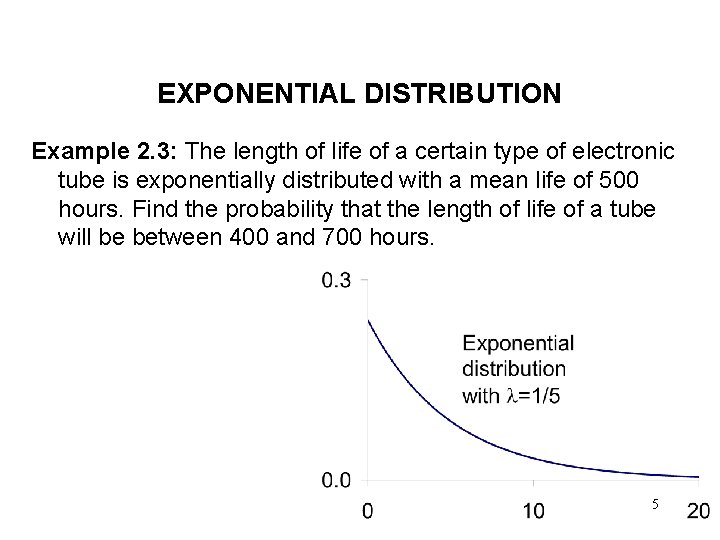
EXPONENTIAL DISTRIBUTION Example 2. 3: The length of life of a certain type of electronic tube is exponentially distributed with a mean life of 500 hours. Find the probability that the length of life of a tube will be between 400 and 700 hours. 5

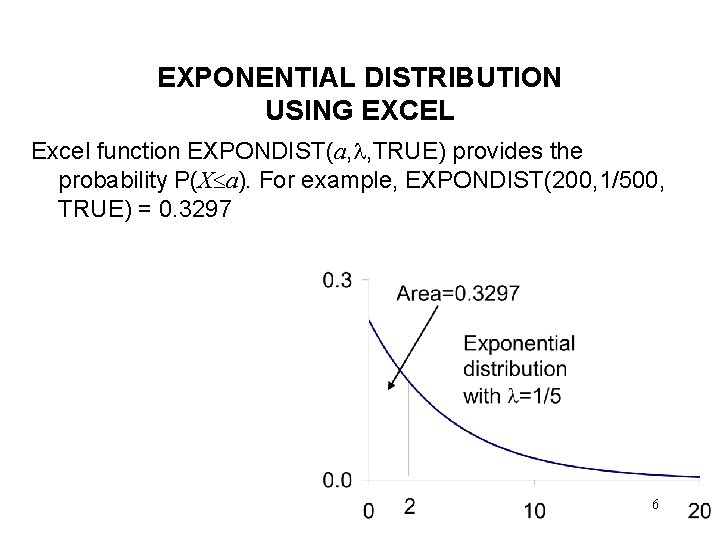
EXPONENTIAL DISTRIBUTION USING EXCEL Excel function EXPONDIST(a, , TRUE) provides the probability P(X a). For example, EXPONDIST(200, 1/500, TRUE) = 0. 3297 6

NOTE • Application: – Uniform distribution • Used to generate other distributions – Normal distribution • Sum of a large number of random numbers – Normal distribution is the most widely used distribution perhaps because of this property. – If a quantity is obtained by summing up some other randomly occurring quantities, then it is very likely that the sum will be normally distributed 7

NOTE – Exponential distribution • Service times, inter-arrival times, etc. are usually observed to be exponentially distributed • If the inter-arrival times are exponentially distributed, then number of arrivals follows Poisson distribution and vice versa • The exponential distribution has an interesting property called the memory less property: Assume that the inter-arrival time of taxi cabs are exponentially distributed and that the probability that a taxi cab will arrive after 1 minute is 0. 8. The above probability does not change even if it is given that a person is 8 waiting for an hour!

READING AND EXERCISES • Reading: pp. 277 -280 • Exercises: 7. 26, 7. 32 9