Exponential and Logarithmic Functions 5 Exponential Functions Logarithmic




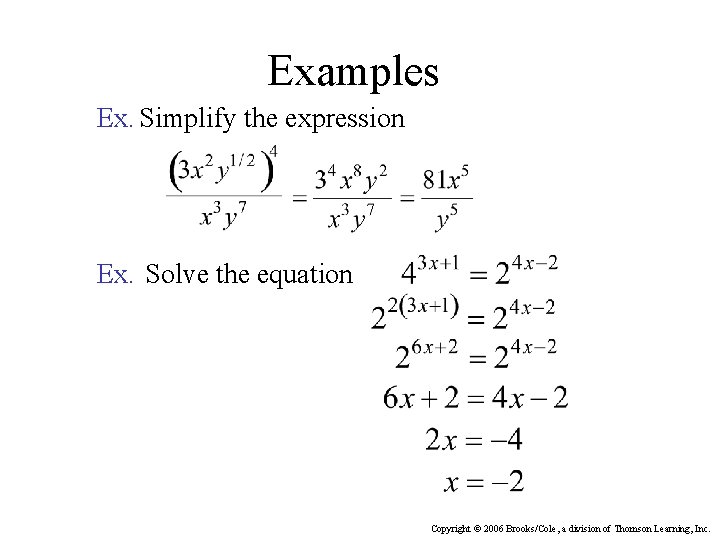

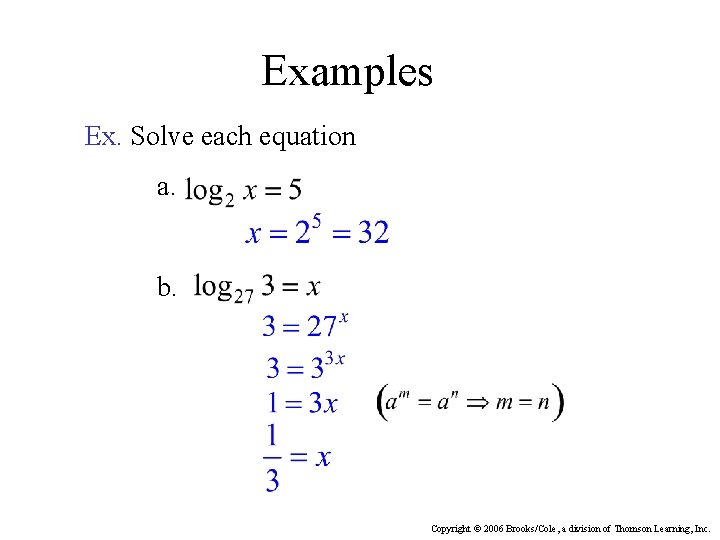



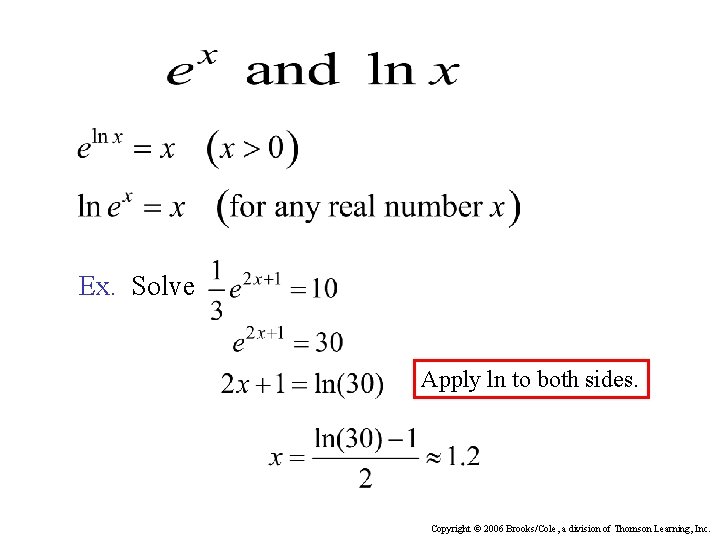






















- Slides: 36

Exponential and Logarithmic Functions 5 • Exponential Functions • Logarithmic Functions • Compound Interest • Differentiation of Exponential Functions • Differentiation of Logarithmic Functions • Exponential Functions as Mathematical Models Copyright © 2006 Brooks/Cole, a division of Thomson Learning, Inc.

Exponential Function An exponential function with base b and exponent x is defined by y Ex. x 0 1 2 y 1 3 9 Domain: All reals (0, 1) Range: y > 0 x Copyright © 2006 Brooks/Cole, a division of Thomson Learning, Inc.

Laws of Exponents Law Example Copyright © 2006 Brooks/Cole, a division of Thomson Learning, Inc.

Properties of the Exponential Function 1. The domain is 2. The range is (0, . ). 3. It passes through (0, 1). 4. It is continuous everywhere. 5. If b > 1 it is increasing on If b < 1 it is decreasing on . . Copyright © 2006 Brooks/Cole, a division of Thomson Learning, Inc.
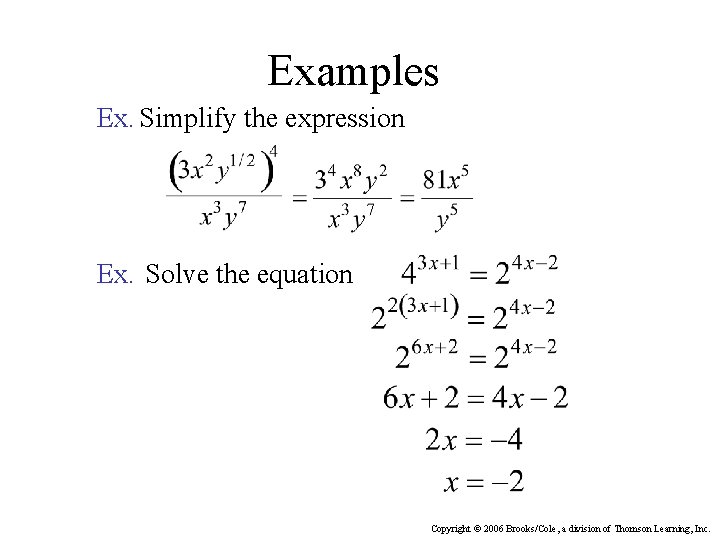
Examples Ex. Simplify the expression Ex. Solve the equation Copyright © 2006 Brooks/Cole, a division of Thomson Learning, Inc.

Logarithms The logarithm of x to the base b is defined by Ex. Copyright © 2006 Brooks/Cole, a division of Thomson Learning, Inc.
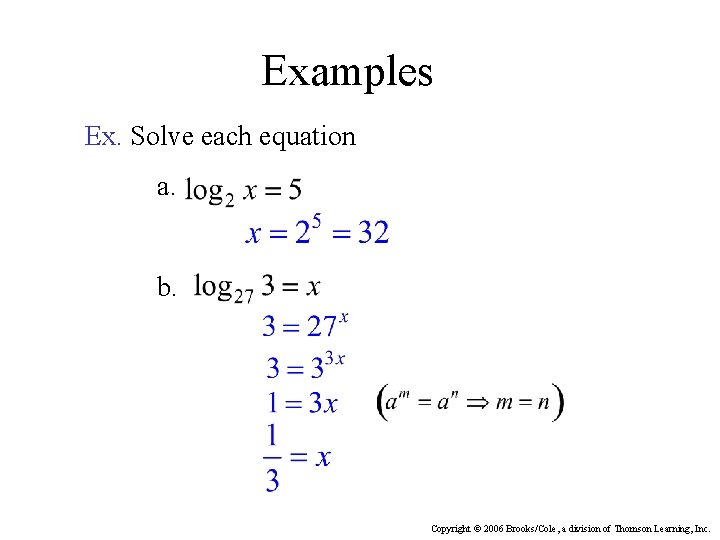
Examples Ex. Solve each equation a. b. Copyright © 2006 Brooks/Cole, a division of Thomson Learning, Inc.

Laws of Logarithms Notation: Common Logarithm Natural Logarithm Copyright © 2006 Brooks/Cole, a division of Thomson Learning, Inc.

Example Use the laws of logarithms to simplify the expression: Copyright © 2006 Brooks/Cole, a division of Thomson Learning, Inc.

Logarithmic Function The logarithmic function of x to the base b is defined by Properties: 1. 2. 3. 4. 5. Domain: (0, ) Range: x-intercept: (1, 0) Continuous on (0, ) Increasing on (0, ) if b > 1 Decreasing on (0, ) if b < 1 Copyright © 2006 Brooks/Cole, a division of Thomson Learning, Inc.

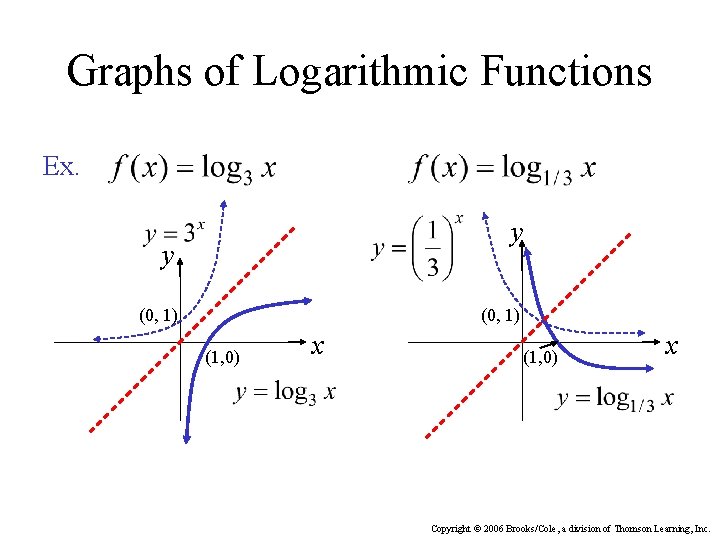
Graphs of Logarithmic Functions Ex. y y (0, 1) (1, 0) x Copyright © 2006 Brooks/Cole, a division of Thomson Learning, Inc.
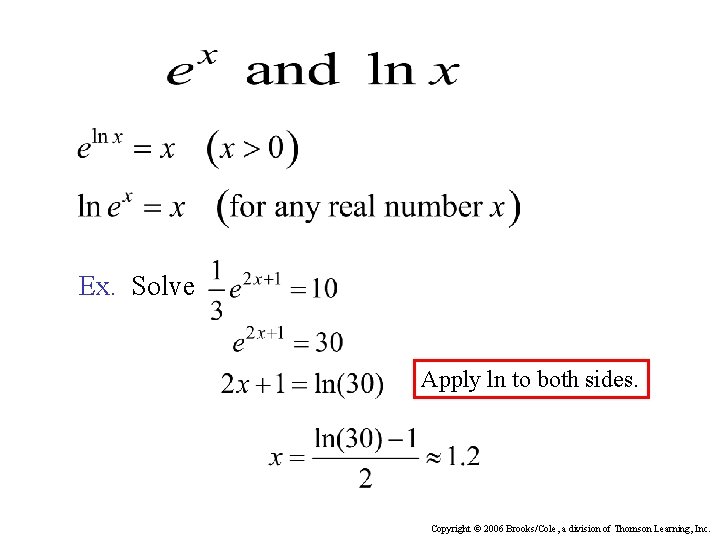
Ex. Solve Apply ln to both sides. Copyright © 2006 Brooks/Cole, a division of Thomson Learning, Inc.

Example A normal child’s systolic blood pressure may be approximated by the function where p(x) is measured in millimeters of mercury, x is measured in pounds, and m and b are constants. Given that m = 19. 4 and b = 18, determine the systolic blood pressure of a child who weighs 92 lb. Copyright © 2006 Brooks/Cole, a division of Thomson Learning, Inc.

Compound Interest Formula A = The accumulated amount after mt periods P = Principal r = Nominal interest rate per year m = Number of periods/year t = Number of years Copyright © 2006 Brooks/Cole, a division of Thomson Learning, Inc.

Example Find the accumulated amount of money after 5 years if $4300 is invested at 6% per year compounded quarterly. = $5791. 48 Copyright © 2006 Brooks/Cole, a division of Thomson Learning, Inc.

Example How long will it take an investment of $10, 000 to grow to $15, 000 if it earns an interest at the rate of 12% / year compounded quarterly? Copyright © 2006 Brooks/Cole, a division of Thomson Learning, Inc.

Effective Rate of Interest reff = Effective rate of interest r = Nominal interest rate/year m = number of conversion periods/year Ex. Find the effective rate of interest corresponding to a nominal rate of 6. 5% per year, compounded monthly. It is about 6. 7% per year. Copyright © 2006 Brooks/Cole, a division of Thomson Learning, Inc.

Present Value Formula for Compound Interest A = The accumulated amount after mt periods P = Principal r = Nominal interest rate/year m = Number of periods/year t = Number of years Copyright © 2006 Brooks/Cole, a division of Thomson Learning, Inc.

Example Find the present value of $4800 due in 6 years at an interest rate of 9% per year compounded monthly. Copyright © 2006 Brooks/Cole, a division of Thomson Learning, Inc.

Continuous Compound Interest Formula A = The accumulated amount after t years P = Principal r = Nominal interest rate per year t = Number of years Copyright © 2006 Brooks/Cole, a division of Thomson Learning, Inc.

Example Find the accumulated amount of money after 25 years if $7500 is invested at 12% per year compounded continuously. Copyright © 2006 Brooks/Cole, a division of Thomson Learning, Inc.

Differentiation of Exponential Functions Derivative of Exponential Function Chain Rule for Exponential Functions If f (x) is a differentiable function, then Copyright © 2006 Brooks/Cole, a division of Thomson Learning, Inc.

Examples Find the derivative of Find the relative extrema of + Relative Min. f (0) = 0 Relative Max. f (-1) = – -1 + 0 x Copyright © 2006 Brooks/Cole, a division of Thomson Learning, Inc.

Differentiation of Logarithmic Functions Derivative of Exponential Function Chain Rule for Exponential Functions If f (x) is a differentiable function, then Copyright © 2006 Brooks/Cole, a division of Thomson Learning, Inc.

Examples Find the derivative of Find an equation of the tangent line to the graph of Slope: Equation: Copyright © 2006 Brooks/Cole, a division of Thomson Learning, Inc.

Logarithmic Differentiation 1. Take the Natural Logarithm on both sides of the equation and use the properties of logarithms to write as a sum of simpler terms. 2. Differentiate both sides of the equation with respect to x. 3. Solve the resulting equation for . Copyright © 2006 Brooks/Cole, a division of Thomson Learning, Inc.

Examples Use logarithmic differentiation to find the derivative of Apply ln Properties of ln Differentiate Solve Copyright © 2006 Brooks/Cole, a division of Thomson Learning, Inc.

Exponential Growth/Decay Models A quantity Q whose rate of growth/decay at any time t is directly proportional to the amount present at time t can be modeled by: Growth Decay Q 0 is the initial quantity k is the growth/decay constant Copyright © 2006 Brooks/Cole, a division of Thomson Learning, Inc.

Example A certain bacteria culture experiences exponential growth. If the bacteria numbered 20 originally and after 4 hours there were 120, find the number of bacteria present after 6 hours. Copyright © 2006 Brooks/Cole, a division of Thomson Learning, Inc.

Learning Curves An exponential function may be applied to certain types of learning processes with the model: C, A, k are positive constants y y=C x Copyright © 2006 Brooks/Cole, a division of Thomson Learning, Inc.

Example Suppose that the temperature T, in degrees Fahrenheit, of an object after t minutes can be modeled using the following equation: 1. Find the temperature of the object after 5 minutes. 2. Find the time it takes for the temperature of the object to reach 190°. Copyright © 2006 Brooks/Cole, a division of Thomson Learning, Inc.

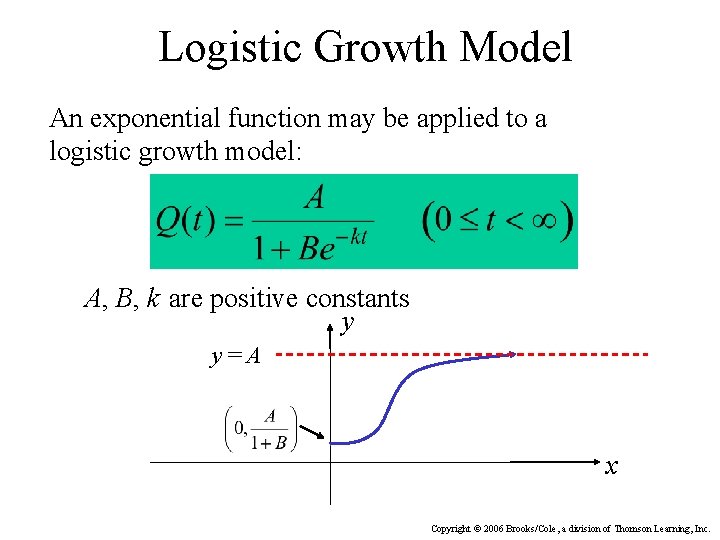
Logistic Growth Model An exponential function may be applied to a logistic growth model: A, B, k are positive constants y y=A x Copyright © 2006 Brooks/Cole, a division of Thomson Learning, Inc.

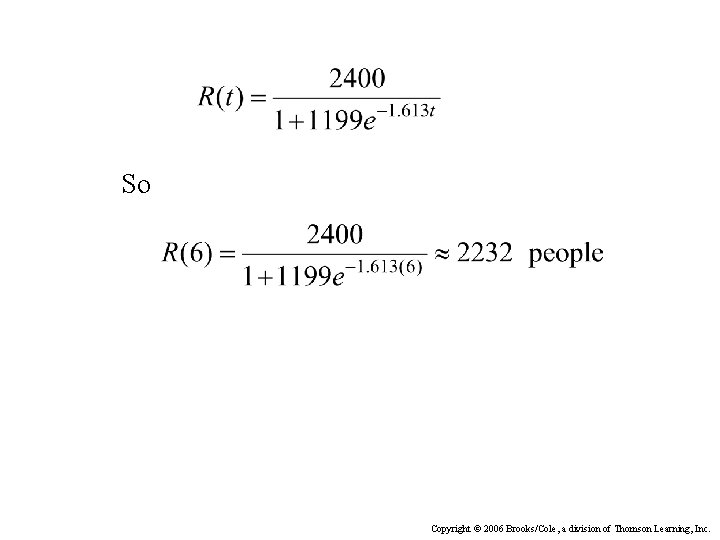
Example The number of people R, in a small school district who have heard a particular rumor after t days can be modeled by: If 10 people know the rumor after 1 day, find the number who heard it after 6 days. … Copyright © 2006 Brooks/Cole, a division of Thomson Learning, Inc.

So Copyright © 2006 Brooks/Cole, a division of Thomson Learning, Inc.

Example The number of soldiers at Fort Mac. Arthur who contracted influenza after t days during a flu epidemic is approximated by the exponential model: If 40 soldiers contracted the flu by day 7, find how many soldiers contracted the flu by day 15. … Copyright © 2006 Brooks/Cole, a division of Thomson Learning, Inc.

So Copyright © 2006 Brooks/Cole, a division of Thomson Learning, Inc.