Exploring Relationships Between Variables Scatterplots and Correlation Objectives

Exploring Relationships Between Variables Scatterplots and Correlation

Objectives Scatterplots p p p Correlation Scatterplots p Explanatory and response variables p Interpreting scatterplots p r has no units Outliers p r ranges from -1 to +1 p Influential points Categorical variables in scatterplots The correlation coefficient “r” r does not distinguish x and y

Basic Terminology p Univariate data: 1 variable is measured on each sample unit or population unit e. g. height of each student in a sample p Bivariate data: 2 variables are measured on each sample unit or population unit e. g. height and GPA of each student in a sample; (caution: data from 2 separate samples is not bivariate data)

Same goals with bivariate data that we had with univariate data p Graphical displays and numerical summaries p Seek overall patterns and deviations from those patterns p Descriptive measures of specific aspects of the data

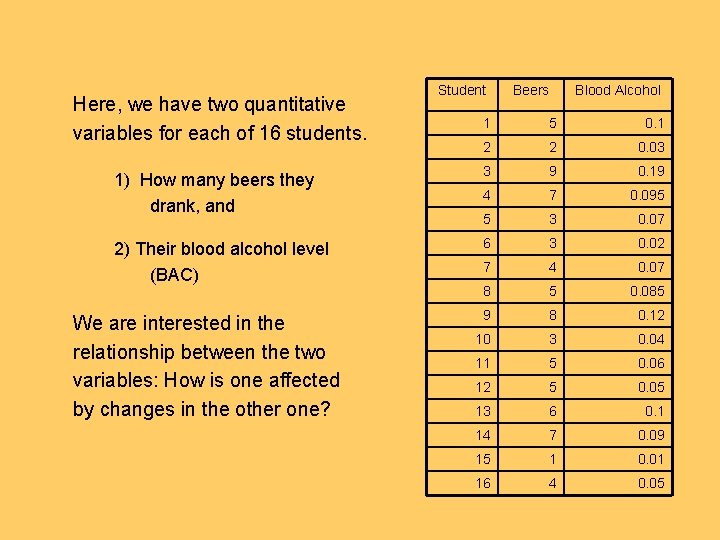
Here, we have two quantitative variables for each of 16 students. Student Beers Blood Alcohol 1 5 0. 1 2 2 0. 03 1) How many beers they drank, and 3 9 0. 19 4 7 0. 095 5 3 0. 07 2) Their blood alcohol level (BAC) 6 3 0. 02 7 4 0. 07 8 5 0. 085 9 8 0. 12 10 3 0. 04 11 5 0. 06 12 5 0. 05 13 6 0. 1 14 7 0. 09 15 1 0. 01 16 4 0. 05 We are interested in the relationship between the two variables: How is one affected by changes in the other one?

Scatterplots p Useful method to graphically describe the relationship between 2 quantitative variables

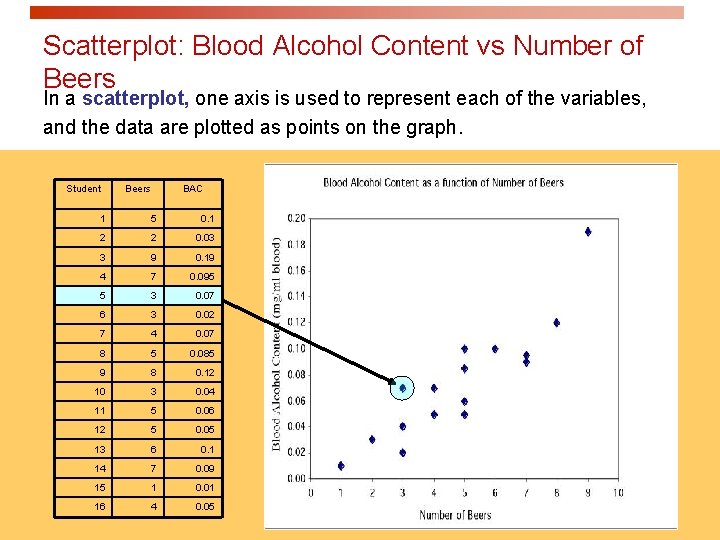
Scatterplot: Blood Alcohol Content vs Number of Beers In a scatterplot, one axis is used to represent each of the variables, and the data are plotted as points on the graph. Student Beers BAC 1 5 0. 1 2 2 0. 03 3 9 0. 19 4 7 0. 095 5 3 0. 07 6 3 0. 02 7 4 0. 07 8 5 0. 085 9 8 0. 12 10 3 0. 04 11 5 0. 06 12 5 0. 05 13 6 0. 1 14 7 0. 09 15 1 0. 01 16 4 0. 05

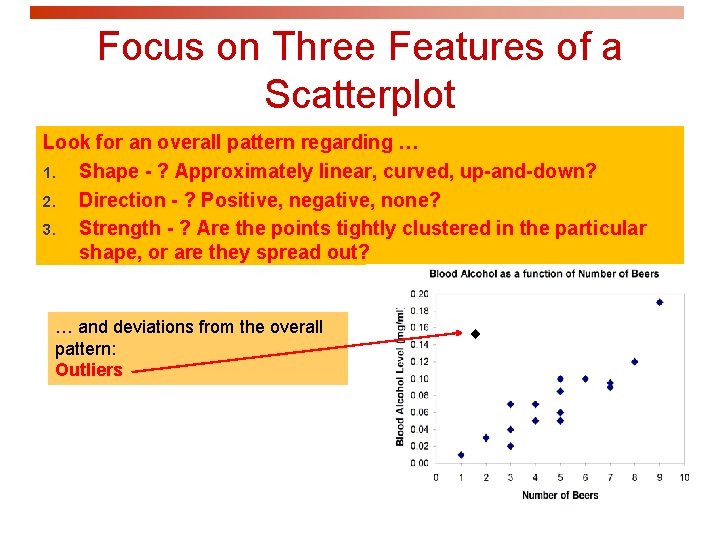
Focus on Three Features of a Scatterplot Look for an overall pattern regarding … 1. Shape - ? Approximately linear, curved, up-and-down? 2. Direction - ? Positive, negative, none? 3. Strength - ? Are the points tightly clustered in the particular shape, or are they spread out? … and deviations from the overall pattern: Outliers

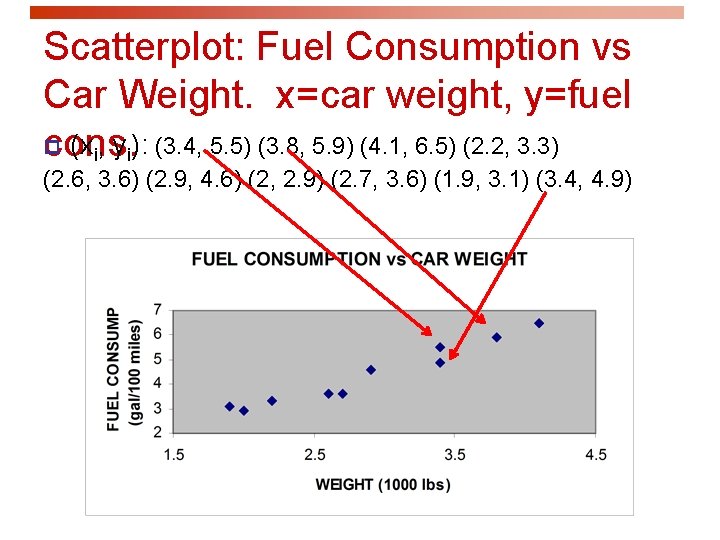
Scatterplot: Fuel Consumption vs Car Weight. x=car weight, y=fuel p (xi, yi): (3. 4, 5. 5) (3. 8, 5. 9) (4. 1, 6. 5) (2. 2, 3. 3) cons. (2. 6, 3. 6) (2. 9, 4. 6) (2, 2. 9) (2. 7, 3. 6) (1. 9, 3. 1) (3. 4, 4. 9)

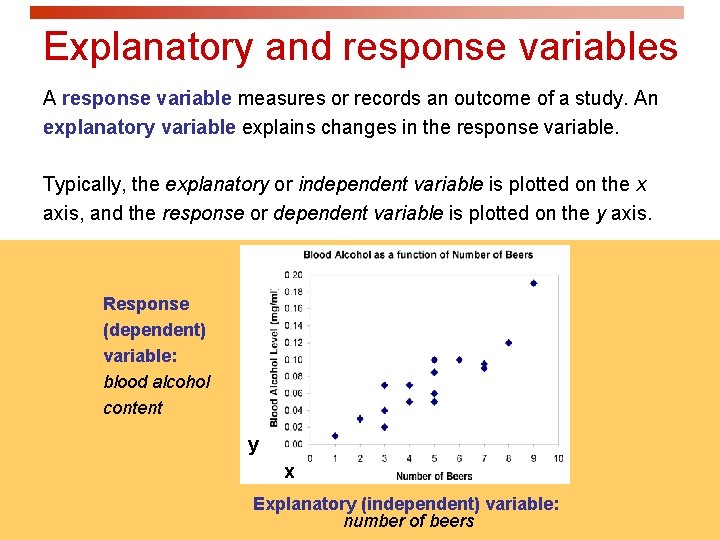
Explanatory and response variables A response variable measures or records an outcome of a study. An explanatory variable explains changes in the response variable. Typically, the explanatory or independent variable is plotted on the x axis, and the response or dependent variable is plotted on the y axis. Response (dependent) variable: blood alcohol content y x Explanatory (independent) variable: number of beers

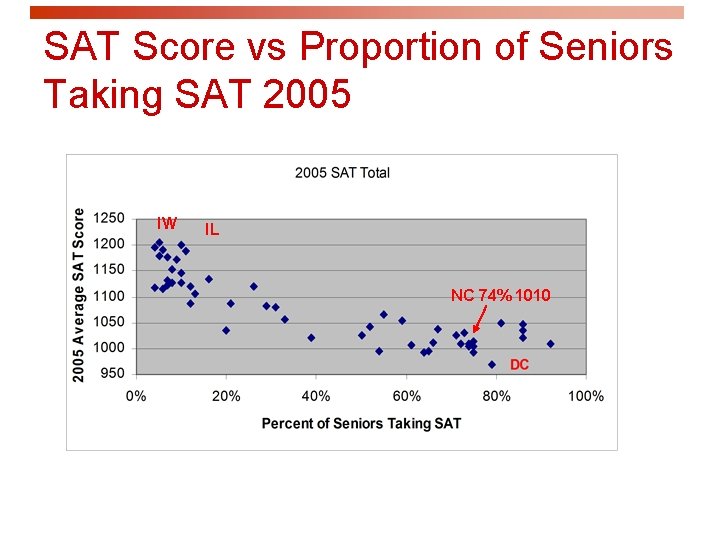
SAT Score vs Proportion of Seniors Taking SAT 2005 IW IL NC 74% 1010

Objectives Correlation p The correlation coefficient “r” p r does not distinguish x and y p r has no units p r ranges from -1 to +1 p Influential points

The correlation coefficient "r" The correlation coefficient is a measure of the direction and strength of the linear relationship between 2 quantitative variables. It is calculated using the mean and the standard deviation of both the x and y variables. Correlation can only be used to describe quantitative variables. Categorical variables don’t have means and standard deviations.

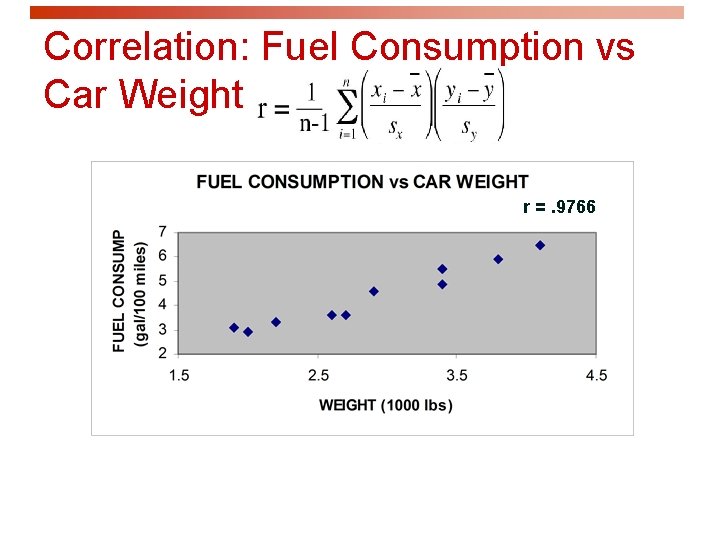
Correlation: Fuel Consumption vs Car Weight r =. 9766

Example: calculating correlation p p (x 1, y 1), (x 2, y 2), (x 3, y 3) (1, 3) (1. 5, 6) (2. 5, 8) Automate calculation of the correlation! (Excel, statcrunch, calculator, etc. )

Properties of Correlation p p p r is a measure of the strength of the linear relationship between x and y. No units [like demand elasticity in economics (-infinity, 0)] -1 < r < 1

Properties (cont. ) r ranges from -1 to+1 "r" quantifies the strength and direction of a linear relationship between 2 quantitative variables. Strength: how closely the points follow a straight line. Direction: is positive when individuals with higher X values tend to have higher values of Y.

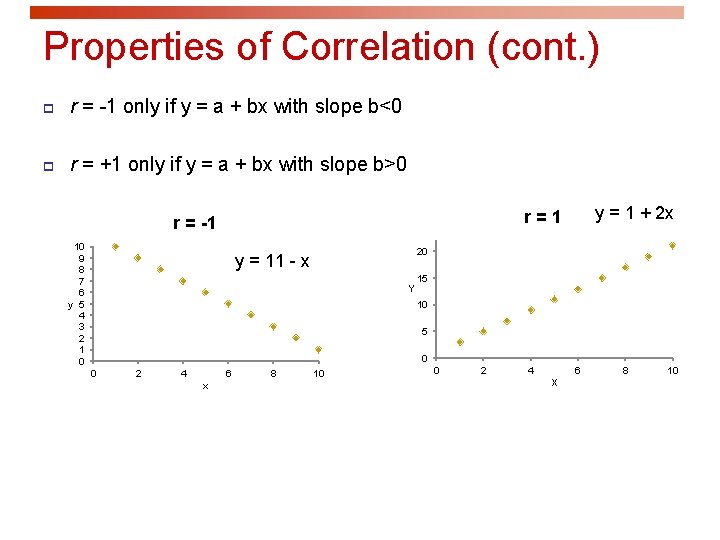
Properties of Correlation (cont. ) p r = -1 only if y = a + bx with slope b<0 p r = +1 only if y = a + bx with slope b>0 y = 1 + 2 x r=1 r = -1 10 9 8 7 6 y 5 4 3 2 1 0 20 y = 11 - x Y 15 10 5 0 0 2 4 6 x 8 10 0 2 4 6 X 8 10

Properties (cont. ) High correlation does not imply cause and effect CARROTS: Hidden terror in the produce department at your neighborhood grocery p Everyone who ate carrots in 1920, if they are still alive, has severely wrinkled skin!!! p Everyone who ate carrots in 1865 is now dead!!! p 45 of 50 17 yr olds arrested in Raleigh for juvenile delinquency had eaten carrots in the 2 weeks prior to their arrest !!!

Properties (cont. ) Cause and Effect p There is a strong positive correlation between the monetary damage caused by structural fires and the number of firemen present at the fire. (More firemen-more damage) p Improper training? Will no firemen present result in the least amount of damage?

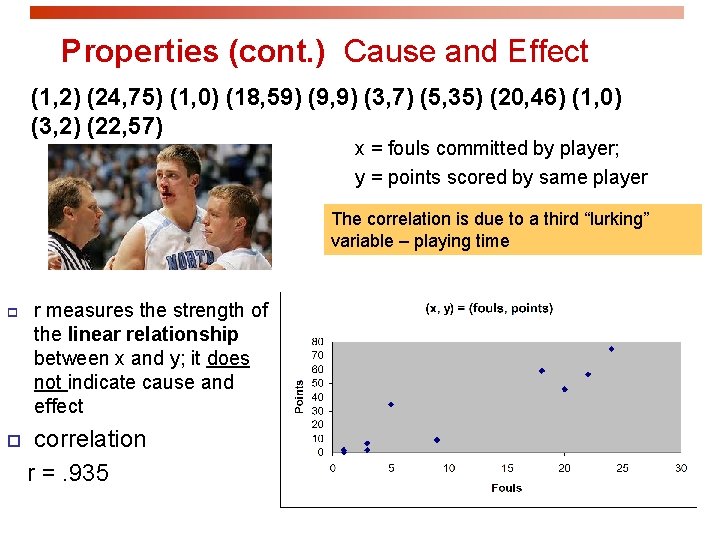
Properties (cont. ) Cause and Effect (1, 2) (24, 75) (1, 0) (18, 59) (9, 9) (3, 7) (5, 35) (20, 46) (1, 0) (3, 2) (22, 57) x = fouls committed by player; y = points scored by same player The correlation is due to a third “lurking” variable – playing time p p r measures the strength of the linear relationship between x and y; it does not indicate cause and effect correlation r =. 935