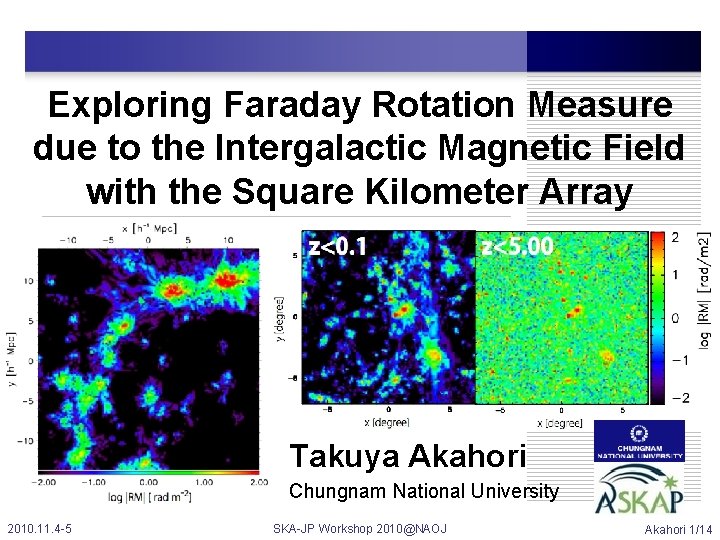
Exploring Faraday Rotation Measure due to the Intergalactic

Exploring Faraday Rotation Measure due to the Intergalactic Magnetic Field with the Square Kilometer Array Takuya Akahori Chungnam National University 2010. 11. 4 -5 SKA-JP Workshop 2010@NAOJ Akahori 1/14

Contents • Introduction • Faraday Rotation Measure (RM) due to the Intergalactic Magnetic Field (IGMF) – Part 1. present-day local universe – Part 2. cosmological effect – Part 3. galactic foreground • Summary and Future References: Akahori, Ryu (2010), Ap. J, 723, 476 ー (2010) to be submitted Akahori, SKA-Japan sub-SWG “Cosmic Magnetism”, Chap. 4 2010. 11. 4 -5 SKA-JP Workshop 2010@NAOJ 2

Introduction: Baryon in our Universe Baryon Phase • ICM (>107 K) Intra-Cluster Medium • WHIM (105 -7 K) Warm-Hot Intergalactic Medium • Others Baryon Phase Diagram from cosmo. simulation (Piro+ 07) Ionized Medium ICM/WHIM 2010. 11. 4 -5 Magnetized? Inter-Galactic Magnetic Field SKA-JP Workshop 2010@NAOJ IGMF 3

Introduction: IGMF and RM Evidences of Magnetization • ICM: RM ~100 [rad m-2] IGMF ~1 -10 [μG] – Kolmogorov? (Vogt & Ensslin 05; Guidetti+ 08; Bonafede+ 10) WHIM: RM < 10 [rad m-2] ? IGMF ~ ? • WHIM: RM < 10 [rad m ] ? IGMF ~ ? Where is the large-scale structure? RM through the ICM Govoni+ (10) All sky RM map Taylor, Stil, Sunstrum (09) IGMF remains largely unknown 2010. 11. 4 -5 SKA-JP Workshop 2010@NAOJ 4

Model: Our Model for the IGMF • Goal: Predict RM of WHIM & test it by future obs. • Method: Simulation of the cosmological structure formation + turbulence dynamo model (Ryu+ 08) – MHD…still hard to treat evolution of turbulence and amplification of the IGMF correctly 100 h-1 Mpc Energy density turbulence dynamo model 1. vorticity energy εw 2. regard εw as εturb 3. εB/εturb=f(t/teddy) 4. B=(8πεB)1/2 ICM Ryu+ (08) 10 -4μG Ryu+ (08) |B| 10μG WHIM 2010. 11. 4 -5 time [teddy] Cho & Ryu (09) SKA-JP Workshop 2010@NAOJ 5

1 Present-day Local universe: Profiles Log 10 |RM| 2. 0 [rad m-2] 1. 0 0. 0 -1. 0 -2. 0 -50 -25 0 [h-1 Mpc] 25 50 • RM: ~100 (GCs), ~10 (Groups), ~0. 01 -1 (filaments) • RM: a random walk process, peaked at the center 2010. 11. 4 -5 SKA-JP Workshop 2010@NAOJ 6

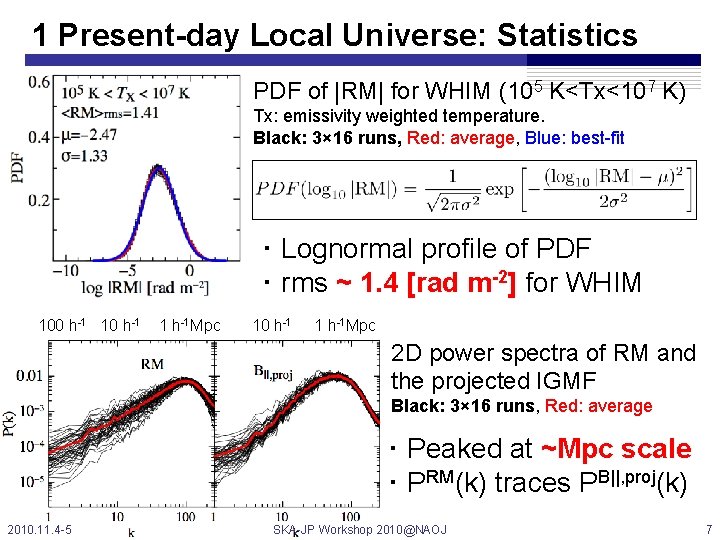
1 Present-day Local Universe: Statistics PDF of |RM| for WHIM (105 K<Tx<107 K) Tx: emissivity weighted temperature. Black: 3× 16 runs, Red: average, Blue: best-fit ・Lognormal profile of PDF ・rms ~ 1. 4 [rad m-2] for WHIM 100 h-1 1 h-1 Mpc 10 h-1 1 h-1 Mpc 2 D power spectra of RM and the projected IGMF Black: 3× 16 runs, Red: average ・Peaked at ~Mpc scale ・PRM(k) traces PB||, proj(k) 2010. 11. 4 -5 SKA-JP Workshop 2010@NAOJ 7

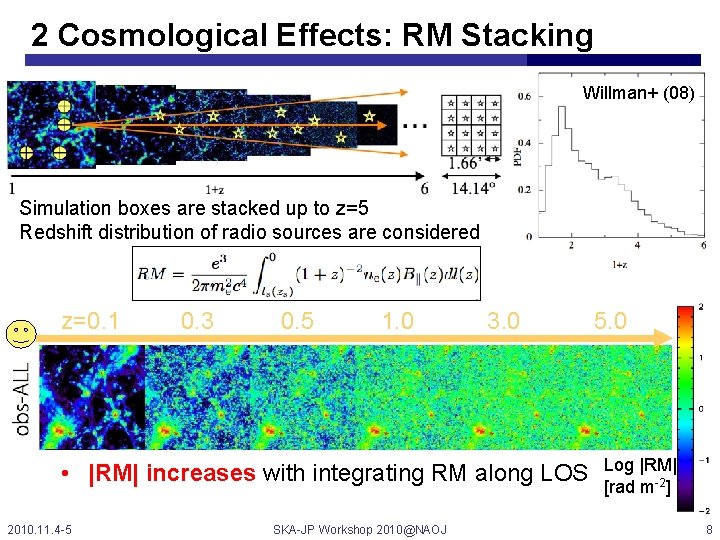
2 Cosmological Effects: RM Stacking Willman+ (08) Simulation boxes are stacked up to z=5 Redshift distribution of radio sources are considered z=0. 1 0. 3 0. 5 1. 0 3. 0 • |RM| increases with integrating RM along LOS 2010. 11. 4 -5 SKA-JP Workshop 2010@NAOJ 5. 0 Log |RM| [rad m-2] 8

2 Cosmological Effecs: rms Value Subtl. of ICM in the integration temperature Tx=4 ke. V ALL CLS TM 7 Average of 200 runs Subtl. of ICM after the integration [rad m-2] RM of WHIM (in) RM of WHIM (after) 2010. 11. 4 -5 1 Mpc Tx=1. 5 ke. V Line of sight 107 K 7 -10 6 -7 TS 8 ALL Map Pixcels w Tx>107 K & Sx>10 -8 e/s/cm 2/sr TS 0 ALL Map Pixcels w Tx>107 K & Sx>10 -10 e/s/cm 2/sr SKA-JP Workshop 2010@NAOJ 9

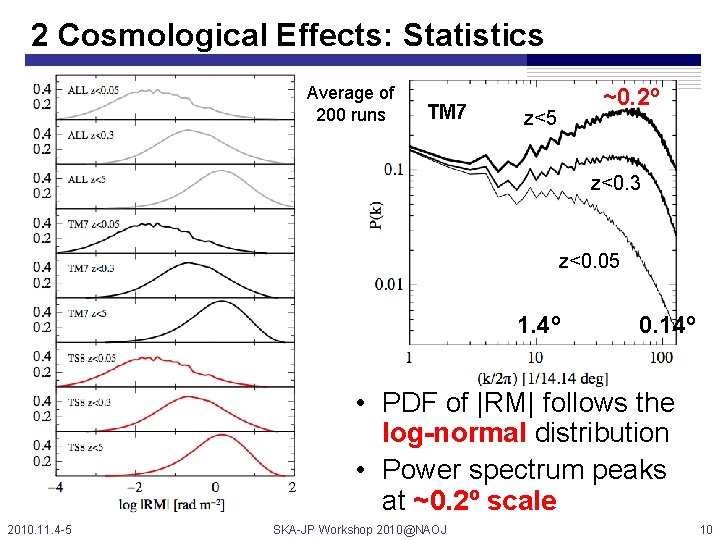
2 Cosmological Effects: Statistics Average of 200 runs TM 7 ~0. 2º z<5 z<0. 3 z<0. 05 1. 4º 0. 14º • PDF of |RM| follows the log-normal distribution • Power spectrum peaks at ~0. 2º scale 2010. 11. 4 -5 SKA-JP Workshop 2010@NAOJ 10

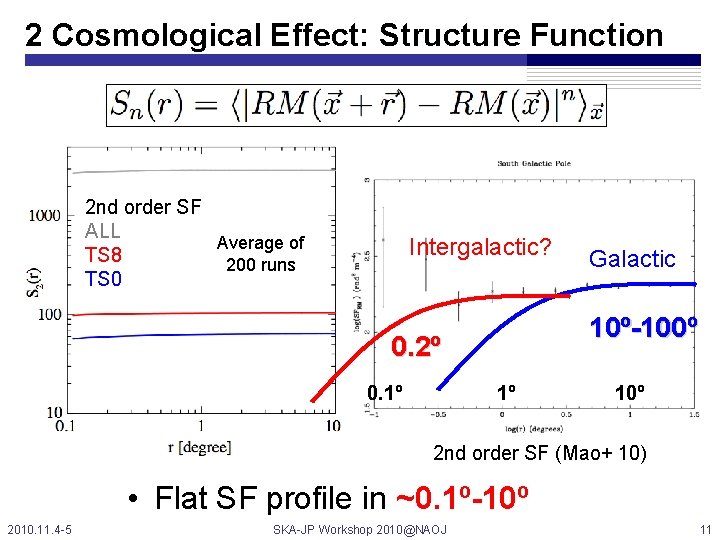
2 Cosmological Effect: Structure Function 2 nd order SF ALL Average of TS 8 200 runs TS 0 Intergalactic? 10º-100º 0. 2º 0. 1º Galactic 1º 10º 2 nd order SF (Mao+ 10) • Flat SF profile in ~0. 1º-10º 2010. 11. 4 -5 SKA-JP Workshop 2010@NAOJ 11

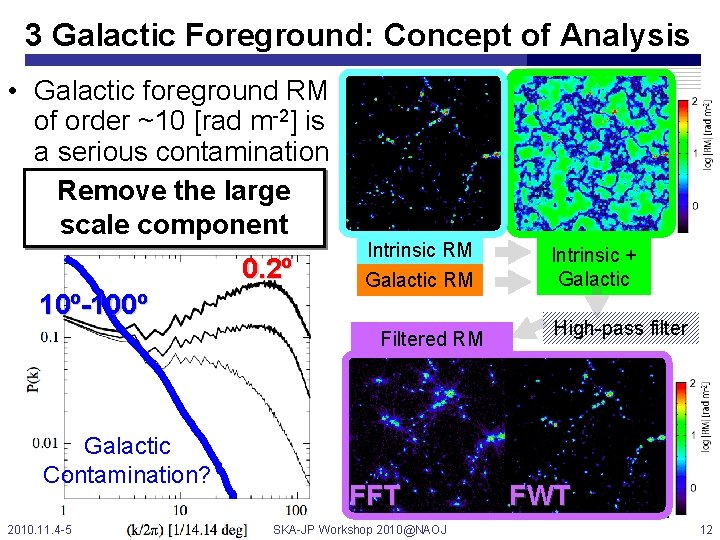
3 Galactic Foreground: Concept of Analysis • Galactic foreground RM of order ~10 [rad m-2] is a serious contamination Remove the large scale component 0. 2º 10º-100º Intrinsic RM Galactic RM Filtered RM Galactic Contamination? 2010. 11. 4 -5 FFT SKA-JP Workshop 2010@NAOJ Intrinsic + Galactic High-pass filter FWT 12

Summary RM in filaments is discussed using a model IGMF • Present-day local universe – rms ~ 1 [rad m-2], lognormal, peak at ~Mpc • Cosmological effects – rms ~ several [rad m-2], lognormal, peak at ~0. 2º • Galactic Foreground – High-pass filters (FFT/FWT) may work well Our estimated RM could be tested with the SKA A concept design for SKA Phase 1 (Garrett+ 10) 2010. 11. 4 -5 SKA-JP Workshop 2010@NAOJ 13

Future • Wide-band observation – RM ranges from ~0. 1 to ~100 rad m-2 • Collaboration with galaxy community – Modeling of galactic foreground – Development of RM analysis • Participation in projects – ASKAP/POSSUM – Japan SKA consortium SWG – Korea SKA consortium? 2010. 11. 4 -5 SKA-JP Workshop 2010@NAOJ Sofue, Machida, Kudo (10) 14