Exploration of Topological Phases with Quantum Walks Takuya

Exploration of Topological Phases with Quantum Walks Takuya Kitagawa Mark Rudner Erez Berg Yutaka Shikano Eugene Demler Harvard University Tokyo Institute of Technology/MIT Harvard University Thanks to Mikhail Lukin Funded by NSF, Harvard-MIT CUA, AFOSR, DARPA, MURI

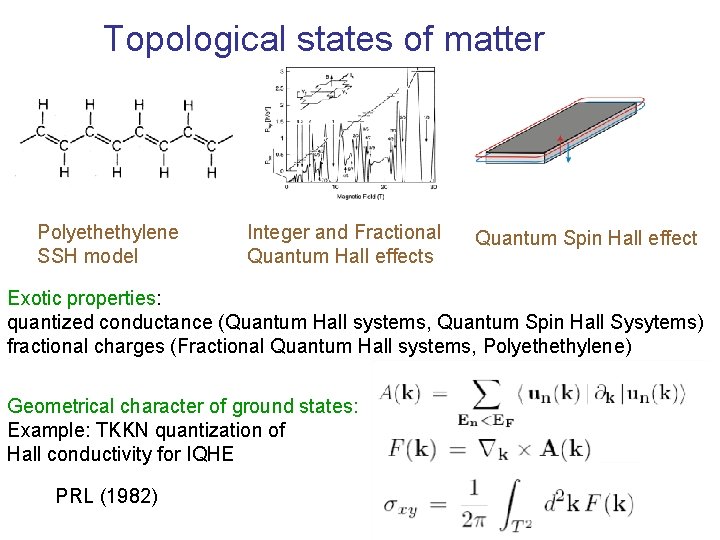
Topological states of matter Polyethethylene SSH model Integer and Fractional Quantum Hall effects Quantum Spin Hall effect Exotic properties: quantized conductance (Quantum Hall systems, Quantum Spin Hall Sysytems) fractional charges (Fractional Quantum Hall systems, Polyethethylene) Geometrical character of ground states: Example: TKKN quantization of Hall conductivity for IQHE PRL (1982)

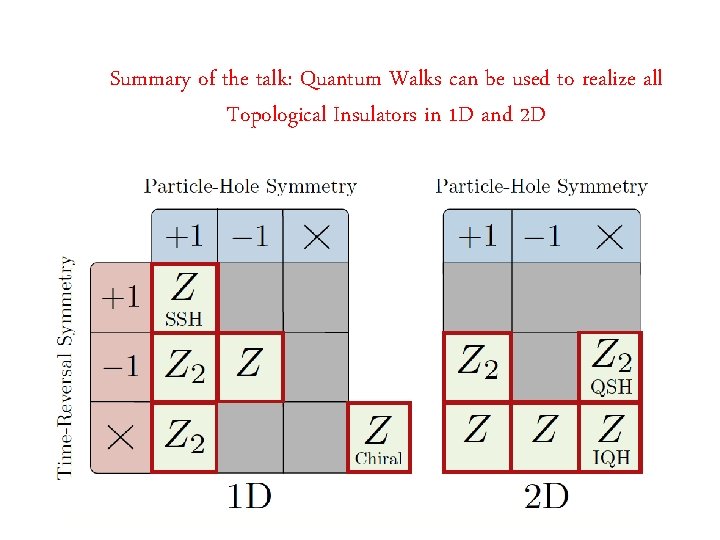
Summary of the talk: Quantum Walks can be used to realize all Topological Insulators in 1 D and 2 D

Outline 1. Introduction to quantum walk What is (discrete time) quantum walk (DTQW)? Experimental realization of quantum walk 2. 1 D Topological phase with quantum walk Hamiltonian formulation of DTQW Topology of DTQW 3. 2 D Topological phase with quantum walk Quantum Hall system without Landau levels Quantum spin Hall system

Discrete quantum walks

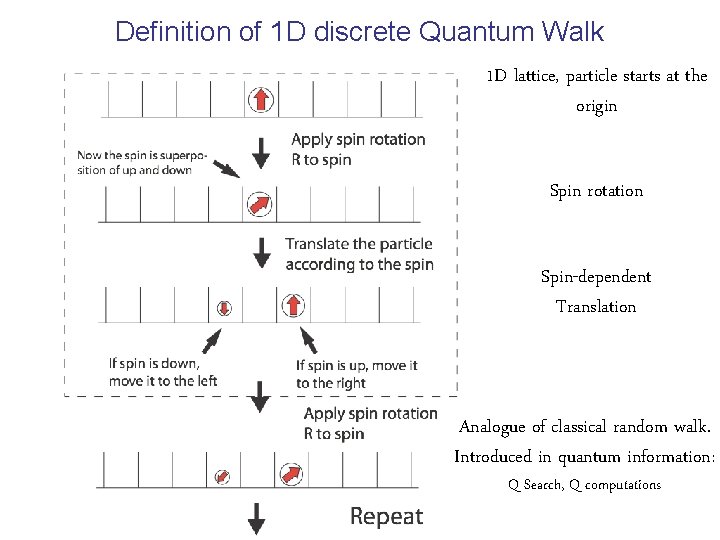
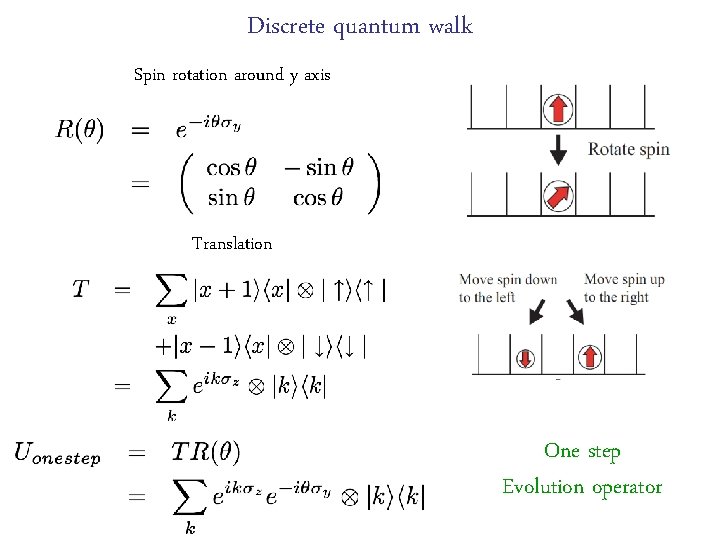
Definition of 1 D discrete Quantum Walk 1 D lattice, particle starts at the origin Spin rotation Spin-dependent Translation Analogue of classical random walk. Introduced in quantum information: Q Search, Q computations

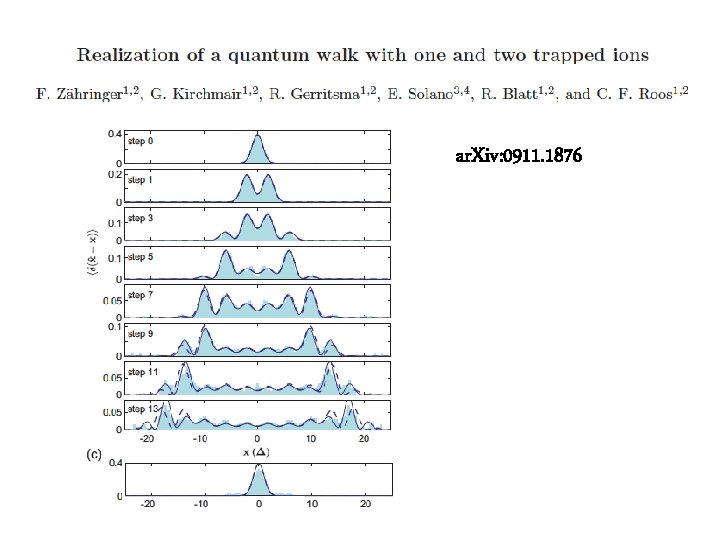
ar. Xiv: 0911. 1876

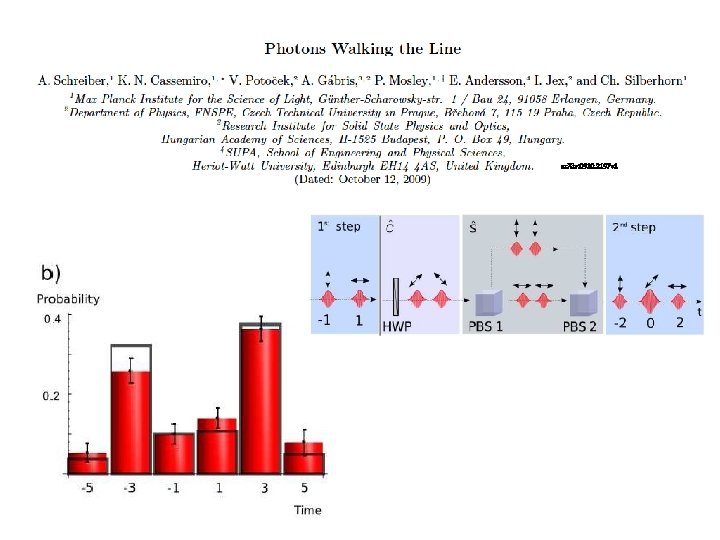
ar. Xiv: 0910. 2197 v 1

Quantum walk in 1 D: Topological phase

Discrete quantum walk Spin rotation around y axis Translation One step Evolution operator

Effective Hamiltonian of Quantum Walk Interpret evolution operator of one step as resulting from Hamiltonian. Stroboscopic implementation of Heff Spin-orbit coupling in effective Hamiltonian

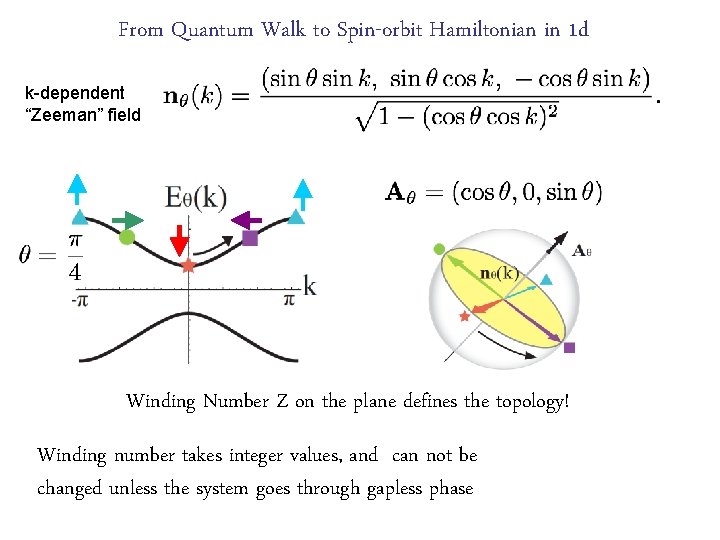
From Quantum Walk to Spin-orbit Hamiltonian in 1 d k-dependent “Zeeman” field Winding Number Z on the plane defines the topology! Winding number takes integer values, and can not be changed unless the system goes through gapless phase

Symmetries of the effective Hamiltonian Chiral symmetry Particle-Hole symmetry For this DTQW, Time-reversal symmetry For this DTQW,

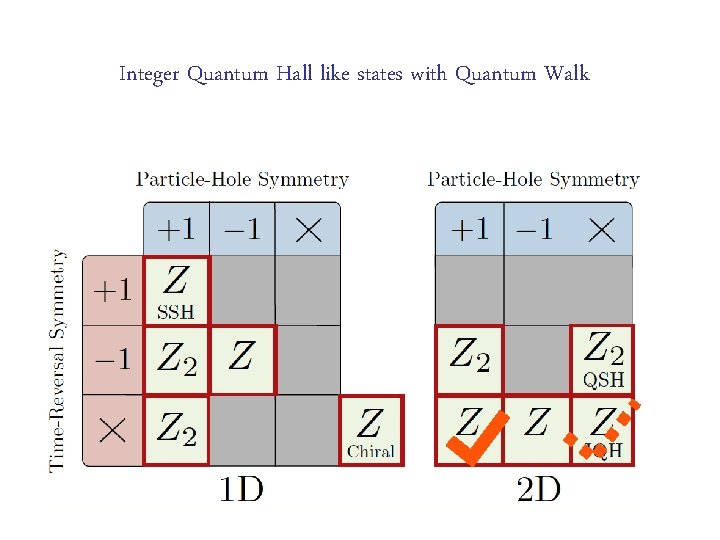
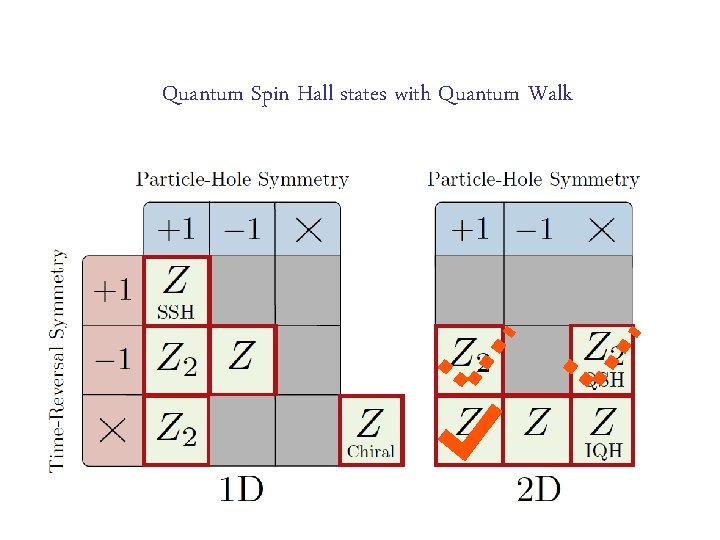
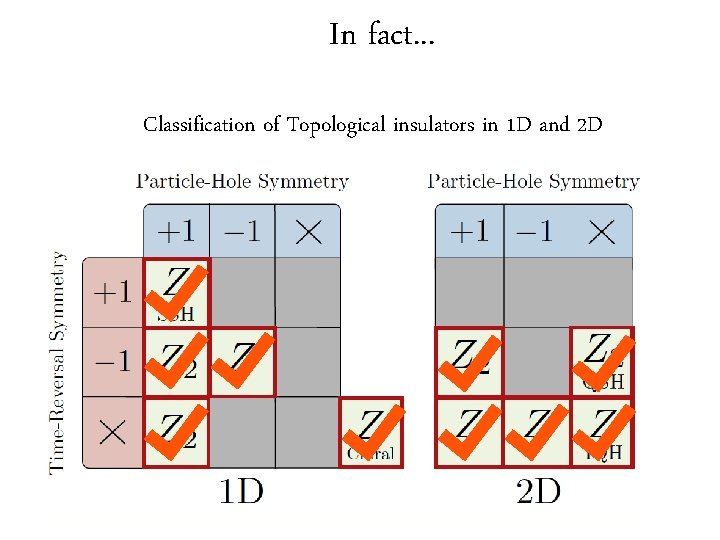
Classification of Topological insulators in 1 D and 2 D

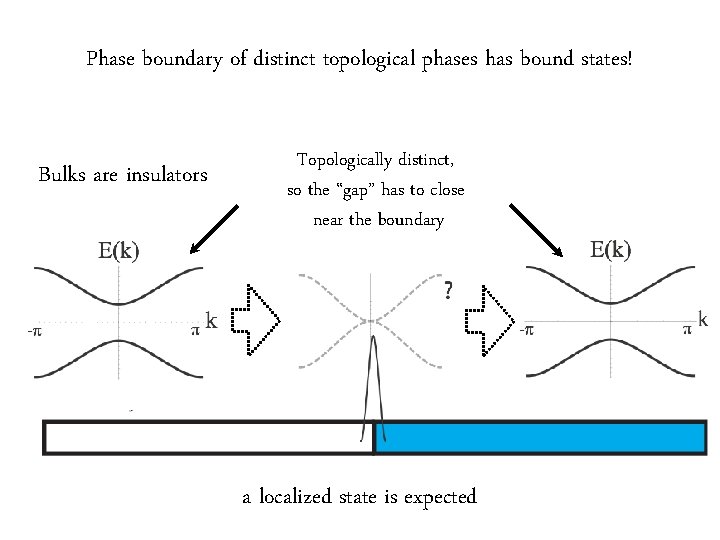
Detection of Topological phases: localized states at domain boundaries

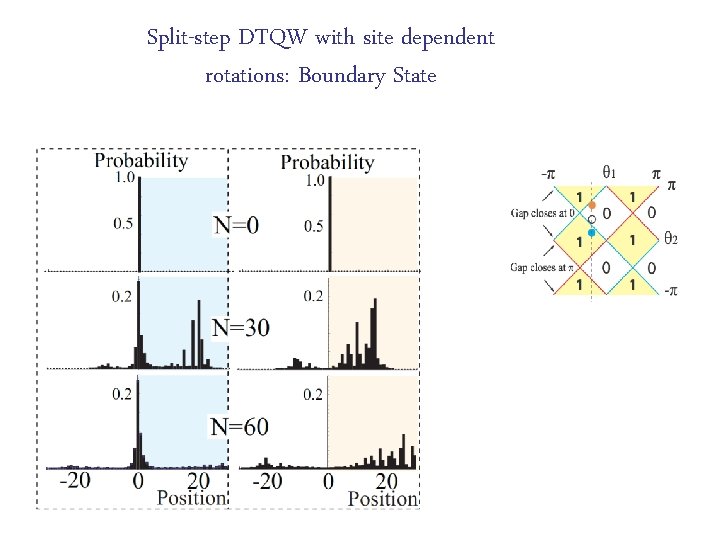
Phase boundary of distinct topological phases has bound states! Bulks are insulators Topologically distinct, so the “gap” has to close near the boundary a localized state is expected

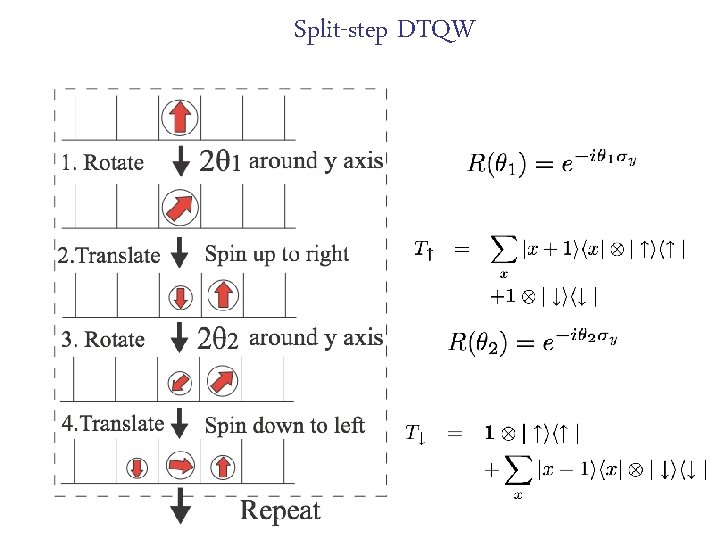
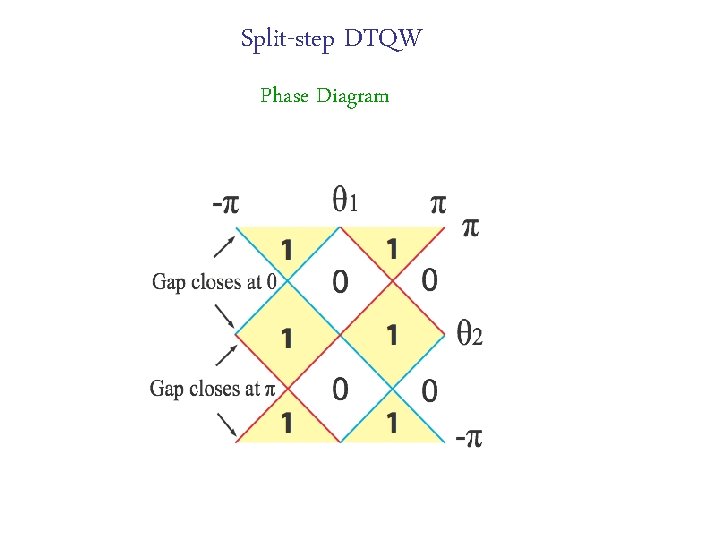
Split-step DTQW

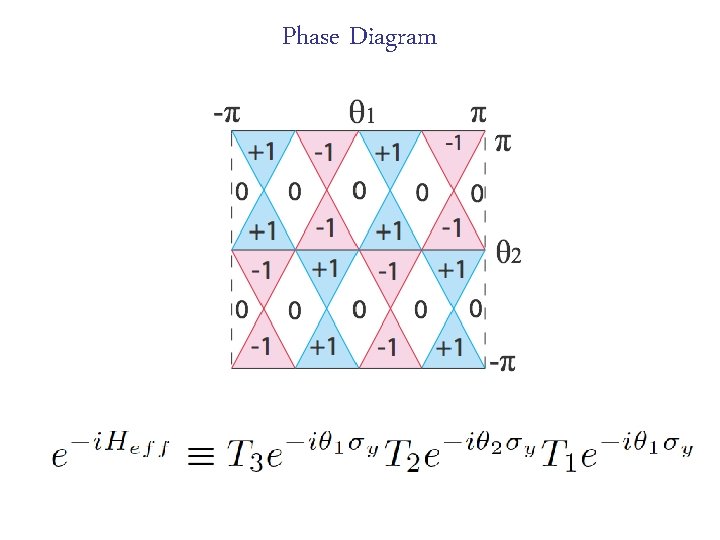
Split-step DTQW Phase Diagram

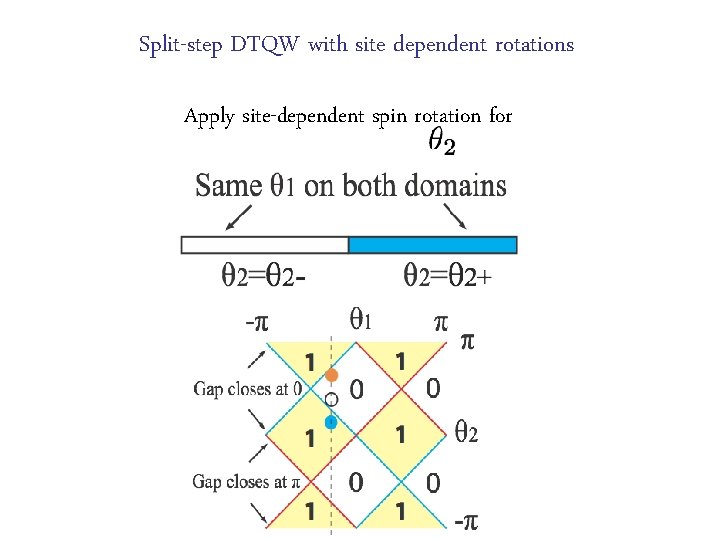
Split-step DTQW with site dependent rotations Apply site-dependent spin rotation for

Split-step DTQW with site dependent rotations: Boundary State

Quantum Hall like states: 2 D topological phase with non-zero Chern number Quantum Hall system

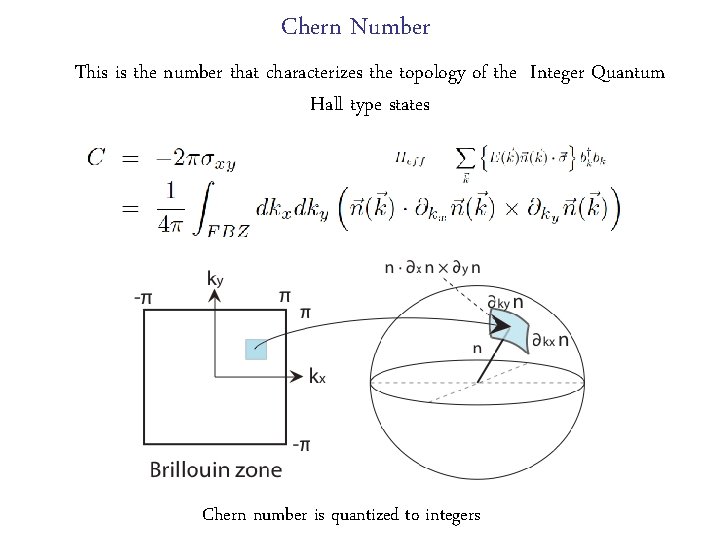
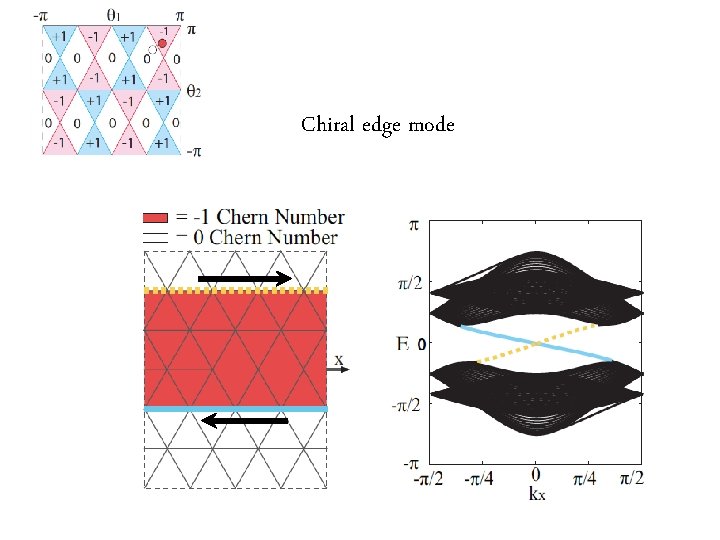
Chern Number This is the number that characterizes the topology of the Integer Quantum Hall type states Chern number is quantized to integers

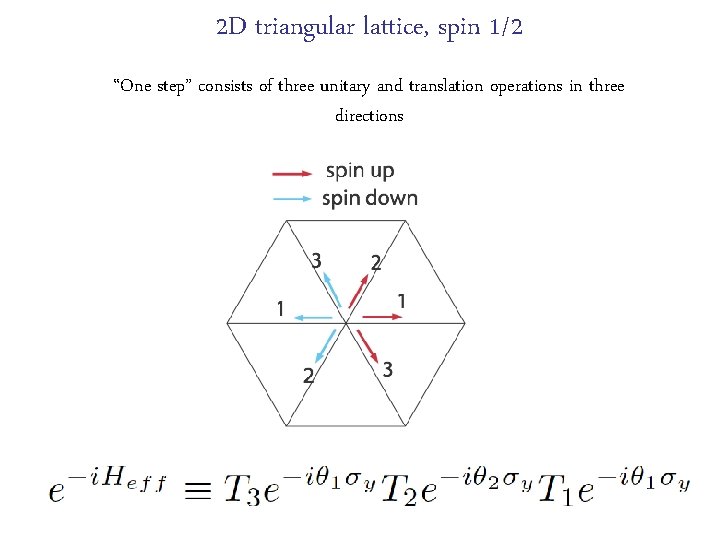
2 D triangular lattice, spin 1/2 “One step” consists of three unitary and translation operations in three directions

Phase Diagram

Chiral edge mode

Integer Quantum Hall like states with Quantum Walk

2 D Quantum Spin Hall-like system with time-reversal symmetry

Introducing time reversal symmetry Introduce another index, A, B Given , time reversal symmetry with is satisfied by the choice of

Take If to be the DTQW for 2 D triangular lattice has non-zero Chern number, the total system is in non-trivial phase of QSH phase

Quantum Spin Hall states with Quantum Walk

In fact. . . Classification of Topological insulators in 1 D and 2 D

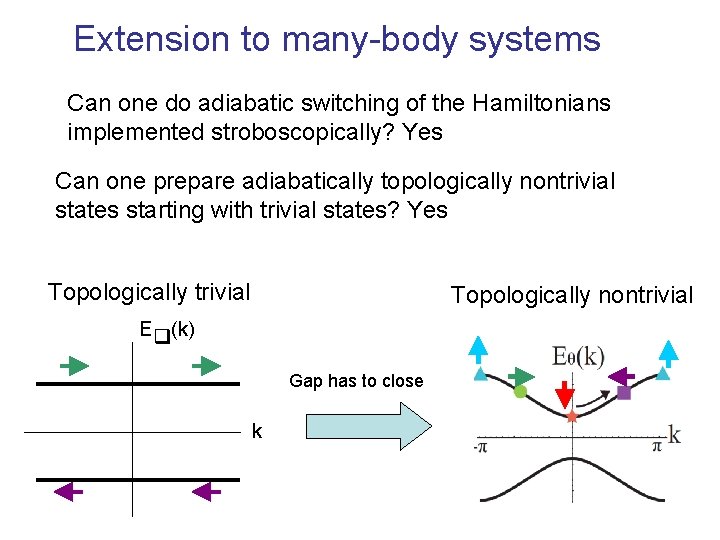
Extension to many-body systems Can one do adiabatic switching of the Hamiltonians implemented stroboscopically? Yes Can one prepare adiabatically topologically nontrivial states starting with trivial states? Yes Topologically trivial Topologically nontrivial Eq(k) Gap has to close k

Conclusions • Quantum walk can be used to realize all of the classified topological insulators in 1 D and 2 D. • Topology of the phase is observable through the localized states at phase boundaries.