Exploration and Apprenticeship Learning in Reinforcement Learning Pieter

Exploration and Apprenticeship Learning in Reinforcement Learning Pieter Abbeel and Andrew Y. Ng Stanford University

Overview n n Reinforcement learning in systems with unknown dynamics. Algorithms such as E 3 (Kearns and Singh, 2002) learn the dynamics by using exploration policies. Aggressive exploration is dangerous for many systems. We show that in apprenticeship learning, when we have a teacher demonstration of the task, this explicit exploration step is unnecessary and instead we can just use exploitation policies. Pieter Abbeel and Andrew Y. Ng

Reinforcement learning formalism n Markov Decision Process (MDP), n n n (S, A, Psa , H, s 0, R). Policy : S ! A. Utility of a policy H n n U( ) = E [ R(st) | ]. t=0 Goal: find policy that maximizes U( ). Pieter Abbeel and Andrew Y. Ng

Motivating example Collect flight data. • Textbook. How model to fly helicopter for data collection? How to ensure that • Specification entire flight envelope is covered by the data collection process? Accurate dynamics model Psa Learn model from data. Pieter Abbeel and Andrew Y. Ng

Learning the dynamical model Have good model of dynamics? n NO YES State-of-the-art: E 3 algorithm, Kearns and Singh (2002). (And its variants/extensions: Kearns and Koller, 1999; Kakade, Kearns and Langford, 2003; Brafman and Tennenholtz, 2002. ) “Exploit” “Explore” Pieter Abbeel and Andrew Y. Ng

Aggressive manual exploration Pieter Abbeel and Andrew Y. Ng

Learning the dynamical model Have good model of impractical: dynamics? Exploration policies are they do not even try to perform well. n NO YES State-of-the-art: E 3 algorithm, Kearns and Singh (2002). Can we avoid explicit exploration and just exploit? (And its variants/extensions: Kearns and Koller, 1999; Kakade, Kearns and Langford, 2003; Brafman and Tennenholtz, 2002. ) “Exploit” “Explore” Pieter Abbeel and Andrew Y. Ng

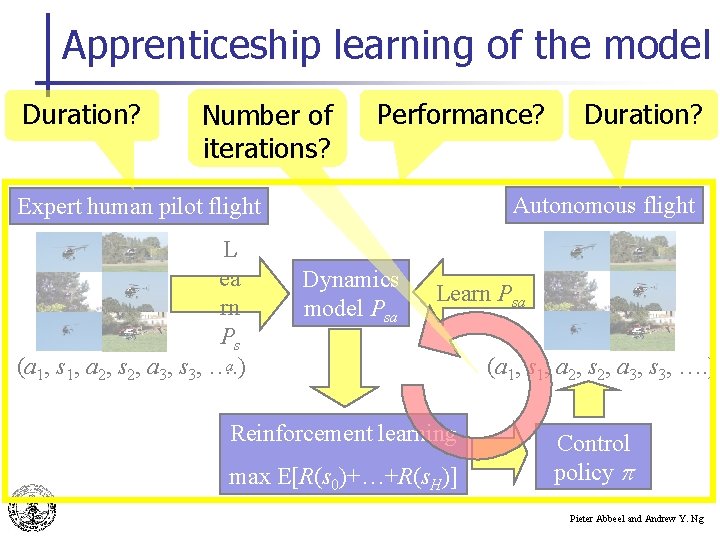
Apprenticeship learning of the model Duration? Number of iterations? Performance? Autonomous flight Expert human pilot flight L ea rn Ps a (a 1, s 1, a 2, s 2, a 3, s 3, …. ) Duration? Dynamics model Psa Learn Psa Reinforcement learning max E[R(s 0)+…+R(s. H)] (a 1, s 1, a 2, s 2, a 3, s 3, …. ) Control policy Pieter Abbeel and Andrew Y. Ng

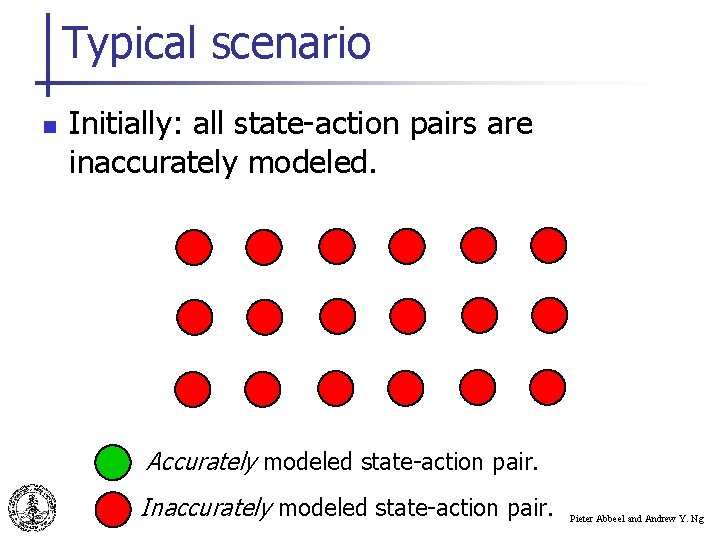
Typical scenario n Initially: all state-action pairs are inaccurately modeled. Accurately modeled state-action pair. Inaccurately modeled state-action pair. Pieter Abbeel and Andrew Y. Ng

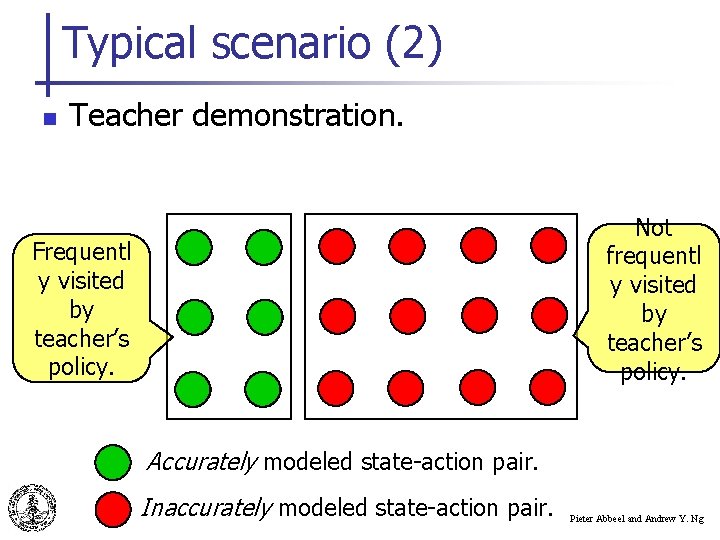
Typical scenario (2) n Teacher demonstration. Not frequentl y visited by teacher’s policy. Frequentl y visited by teacher’s policy. Accurately modeled state-action pair. Inaccurately modeled state-action pair. Pieter Abbeel and Andrew Y. Ng

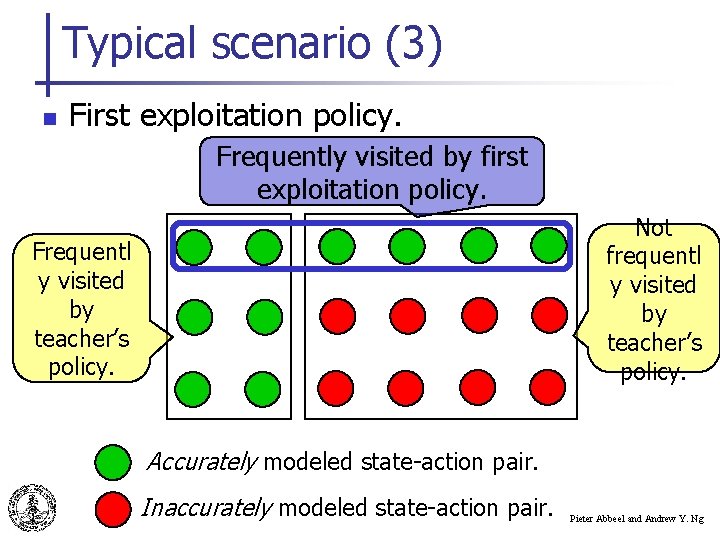
Typical scenario (3) n First exploitation policy. Frequently visited by first exploitation policy. Not frequentl y visited by teacher’s policy. Frequentl y visited by teacher’s policy. Accurately modeled state-action pair. Inaccurately modeled state-action pair. Pieter Abbeel and Andrew Y. Ng

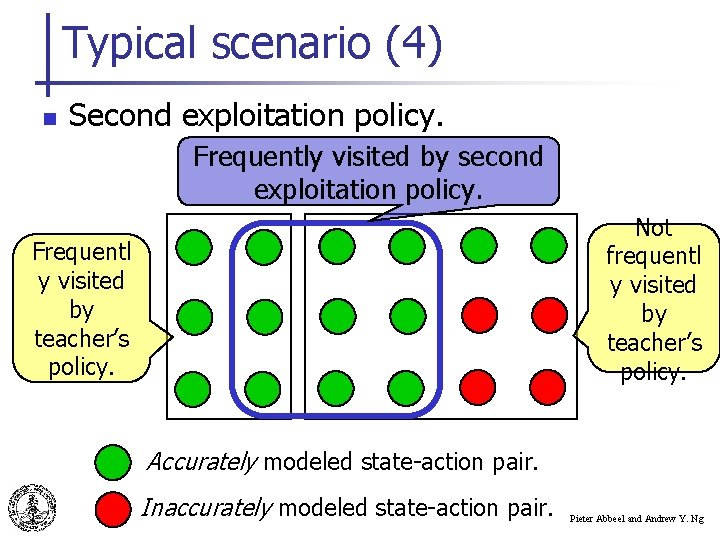
Typical scenario (4) n Second exploitation policy. Frequently visited by second exploitation policy. Not frequentl y visited by teacher’s policy. Frequentl y visited by teacher’s policy. Accurately modeled state-action pair. Inaccurately modeled state-action pair. Pieter Abbeel and Andrew Y. Ng

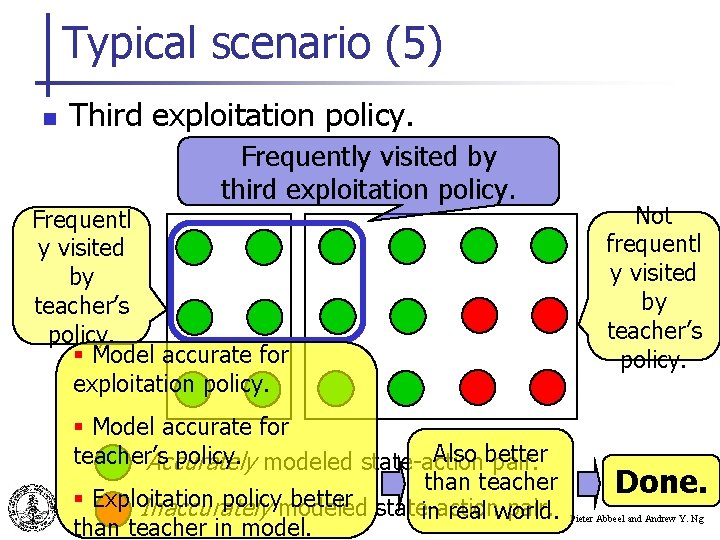
Typical scenario (5) n Third exploitation policy. Frequently visited by third exploitation policy. Frequentl y visited by teacher’s policy. § Model accurate for exploitation policy. § Model accurate for Also better teacher’s policy. modeled state-action Accurately pair. than teacher § Exploitation policymodeled better state-action Inaccurately pair. in real world. than teacher in model. Not frequentl y visited by teacher’s policy. Done. Pieter Abbeel and Andrew Y. Ng

Two dynamics models n Discrete dynamics: n n Finite S and A. Dynamics Psa are described by state transition probabilities P(s’|s, a). Learn dynamics from data using maximum likelihood. Continuous, linear dynamics: n n n Continuous valued states and actions. (S = <n. S, A = <n. A). st+1 = G (st) + H at + wt. Estimate G, H from data using linear regression. Pieter Abbeel and Andrew Y. Ng

Performance guarantees Let any , > 0 be given. Theorem. For U( ) ¸ U( T) - within N=O(poly(1/ , H, Rmax, )) iterations with probability 1 - , it suffices: Nteacher= (poly(1/ , H, Rmax, )), Nexploit = (poly(1/ , 1/message: , H, Rmax, )). n. Take-home To perform as well as teacher, it suffices: a poly number of iterations a poly number of teacher demonstrations a poly number of trials with each exploitation policy. so long as a demonstration is available, it is =not |S|, |Anecessary | (discrete), to explicitly explore; = n. S, n. A, ||it G||suffices , ||H|| (continuous). to only exploit. Fro Pieter Abbeel and Andrew Y. Ng

Proof idea n n n From initial pilot demonstrations, our model/simulator Psa will be accurate for the part of the state space (s, a) visited by the pilot. Our model/simulator will correctly predict the helicopter’s behavior under the pilot’s policy T. Consequently, there is at least one policy (namely T) that looks capable of flying the helicopter well in our simulation. Thus, each time we solve the MDP using the current model/simulator Psa, we will find a policy that successfully flies the helicopter according to Psa. If, on the actual helicopter, this policy fails to fly the helicopter---despite the model Psa predicting that it should--then it must be visiting parts of the state space that are inaccurately modeled. Hence, we get useful training data to improve the model. This can happen only a small number of times. Pieter Abbeel and Andrew Y. Ng

Learning with non-IID samples n n IID = independent and identically distributed. Our algorithm n n n n All future states depend on current state. Exploitation policies depend on states visited. States visited depend on past exploitation policies. Exploitation policies depend on past exploitation policies. Very complicated non-IID sample generating process. Standard learning theory/convergence bounds (e. g. , Hoeffding inequalities) cannot be used in our setting. Martingales, Azuma’s inequality, optional stopping theorem. Pieter Abbeel and Andrew Y. Ng

Related Work n n n Schaal & Atkeson, 1994: open-loop policy as starting point for devil-sticking, slow exploration of state space. Smart & Kaelbling, 2000: model-free Qlearning, initial updates based on teacher. Supervised learning of a policy from demonstration, e. g. , n n Sammut et al. (1992); Pomerleau (1989); Kuniyhoshi et al. (1994); Amit & Mataric (2002), … Apprenticeship learning for unknown reward function (Abbeel & Ng, 2004). Pieter Abbeel and Andrew Y. Ng

Conclusion n n Reinforcement learning in systems with unknown dynamics. Algorithms such as E 3 (Kearns and Singh, 2002) learn the dynamics by using exploration policies, which are dangerous/impractical for many systems. We show that this explicit exploration step is unnecessary in apprenticeship learning, when we have an initial teacher demonstration of the task. We attain near-optimal performance (compared to the teacher) simply by repeatedly executing “exploitation policies'' that try to maximize rewards. In finite-state MDPs, our algorithm scales polynomially in the number of states; in continuous-state linearly parameterized dynamical systems, it scales polynomially in the dimension of the state space. Pieter Abbeel and Andrew Y. Ng

End of talk, additional slides for poster after this Pieter Abbeel and Andrew Y. Ng

Samples from teacher n n n Dynamics model: st+1 = G (st) + H at + wt Parameter estimates after k samples: (G(k), H(k))= arg min. G, H loss(k)(G, H) k = arg min. G, H (st+1 – (G (st) + H at))2 t=0 Consider: Z(k) = loss(k)(G, H) – E[loss(k)(G, H)] n Then: E[Z(k) | history up to time k-1] = Z(k-1) n n Thus: Z(0), Z(1), … is a martingale sequence. Using Azuma’s inequality (a standard martingale result) we prove convergence. Pieter Abbeel and Andrew Y. Ng

Samples from exploitation policies n Consider: Z(k) = exp(loss(k)(G*, H*) – loss(k)(G, H)) n Then: E[Z(k) | history up to time k-1] = Z(k-1) n n Thus: Z(0), Z(1), … is a martingale sequence. Using the optional stopping theorem (a standard martingale result) we prove true parameters G*, H* outperform G, H with high probability for all k=0, 1, … Pieter Abbeel and Andrew Y. Ng