Explaining the Fallacies Implications for the Roles of












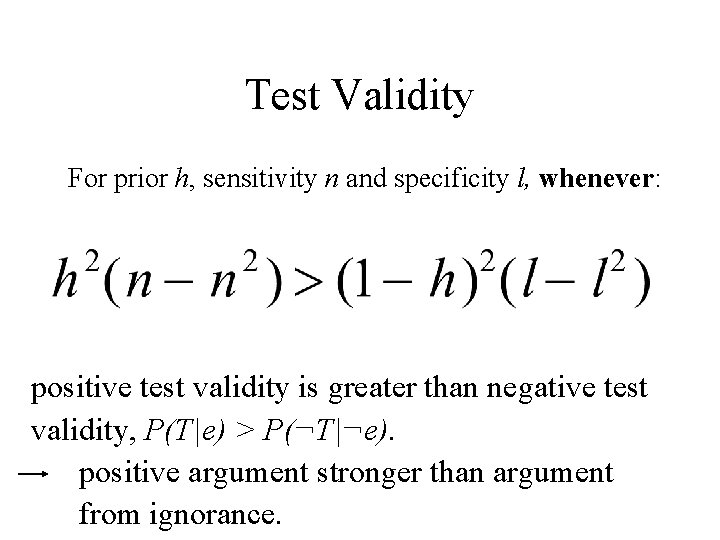

















- Slides: 39

Explaining the Fallacies Implications for the Roles of Probability and Logic in Argumentation Ulrike Hahn Cardiff University Mike Oaksford Birkbeck College London

The Fallacies • Original catalogue Aristotle; additions from middle ages to present time (e. g. , Locke) Catalogue of (some) fallacies: equivocation; irrelevance; circularity; consequent; ad verecundium (authority); ad hominem, ad ignorantiam; ad populum; ad misericordiam; ad consequentiam; ad baculum; post hoc ergo propter hoc; slippery slope arguments

Fallacies Circular arguments: God exists, because the Bible says so, and the Bible is the word of God. Argument from ignorance: Ghosts exist, because nobody has proven that they don’t

Fallacies Circular arguments: God exists, because the Bible says so, and the Bible is the word of God. Argument from ignorance: Ghosts exist, because nobody has proven that they don’t

The Question • why are they fallacious? • can single formal account be given? • can formal account be given for any individual one?

Past Attempts • Logic as objective standard of validity • Classical logics have failed here - fallacies exist in introductory logic texts under header of “informal reasoning fallacies”

Past Attempts • Logic as objective standard of validity • Classical logics have failed here - fallacies exist in introductory logic texts under header of “informal reasoning fallacies” • The problem: – Some fallacies seem logically valid, but nevertheless poor arguments – Many have exceptions that don’t seem quite as bad

Circularity again. . God exists, because God exists

Circularity ctd. • God exists, because the Bible says so, and the Bible is the word of God • Electrons exist because their signature effects can be seen with a particle accelerator

A Bayesian Account of the Argument from ignorance • Ghosts exist, because no-one has proved they don’t • This drug is safe, since no-one has found any side effects Both arguments present a conclusion (C) and evidence (e) • C: Ghosts exist, This drug is safe • e: Nobody has proved Ghosts don’t exist, No evidence that the drug is not safe To calculate the strength of each argument use Bayes’ Theorem:

When are they good arguments? (If drug A were toxic, it would produce toxic effects in legitimate tests) Drug A has not produced toxic effects in such tests Therefore, A is not toxic

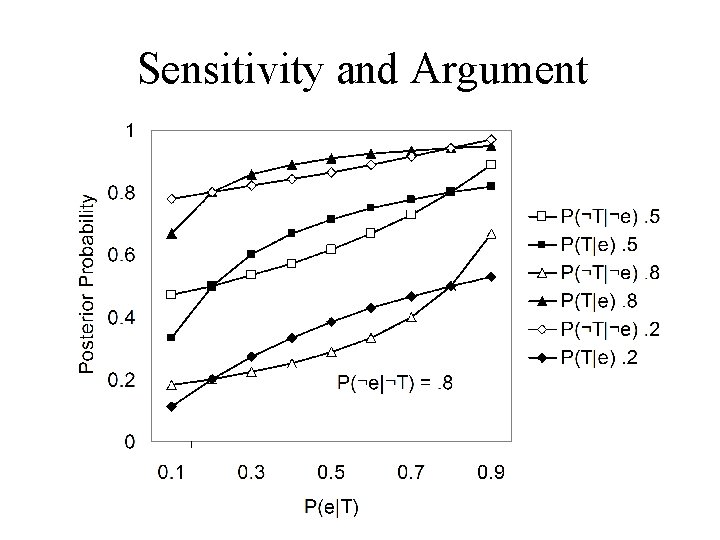
Polarity: positive vs. negative evidence Given: test sensitivity - P(e|T) test specificity - P(¬e|¬T) degree of prior belief in T - P(T) Can derive via Bayes’ theorem: Negative vs. positive test validity: P(¬T|¬e) vs. P(T|e)
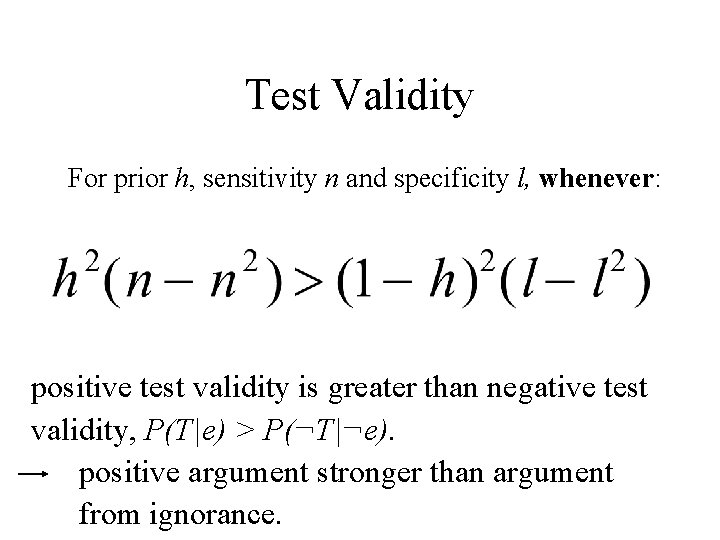
Test Validity For prior h, sensitivity n and specificity l, whenever: positive test validity is greater than negative test validity, P(T|e) > P(¬T|¬e). positive argument stronger than argument from ignorance.

Sensitivity and Argument Strength

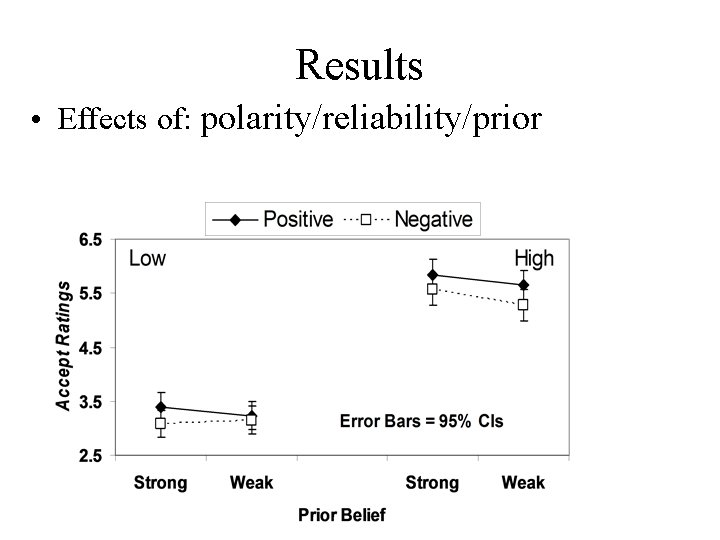
Sample Materials (HOB, 2005) • Brenda: Do you think it is beneficial to privatise public transportation? • Adam: I am fairly convinced that it is beneficial to privatise public transportation. • Brenda: You can be more than fairly convinced; you can be certain that it is beneficial. • Adam: Why do you say that? • Brenda: Because I read a newspaper interview with the members of a non-governmental research body and they said that it is beneficial considering the improved service quality and the reduction in the overall operating costs.

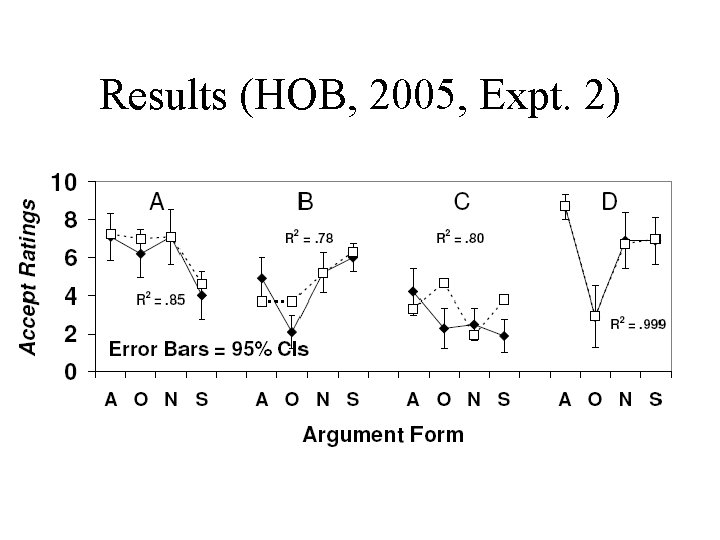
Results • Effects of: polarity/reliability/prior

back to ghosts…: Ghosts exist, because nobody has proven that they don’t !!not just neg. evidence but also 2 opposite polarities: not proven (exist) -> not exist vs. not proven( not exist) -> exist

Epistemic Closure • not(not p) = p • not says (not p) = ? …could say p or nothing at all • not says (not p) ≈ says p

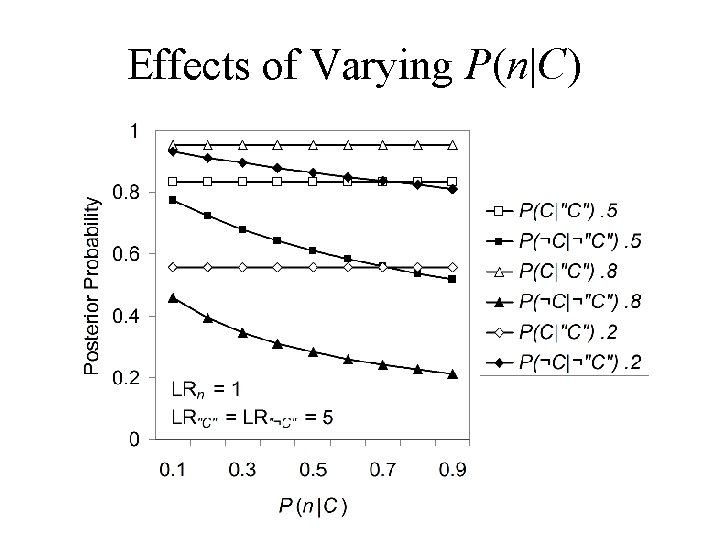
Modelling Epistemic Closure: Saying Nothing • Sources • Either “C, ” “¬C, ” or they say nothing about C, n • Sensitivity = P(“C”|C), Specificity = P(“¬C”|¬C) • Closure • If closed then P(n) = 0 and P(¬“C”) = P(“¬C”) • If not closed P(¬“C”) = P(“¬C”) + P(n)

Effects of Varying P(n|C)

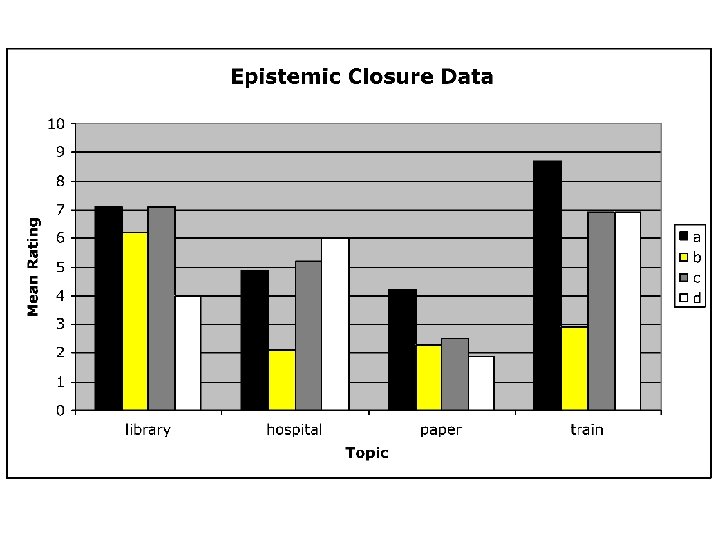
Example: Newspaper reports of secret treaty a: b: c: d: says(exists) -> treaty exists NOT says(NOT exists) -> exists says(NOT exists) –> NOT exists NOT says(exists) – >NOT exists


Results (HOB, 2005, Expt. 2)

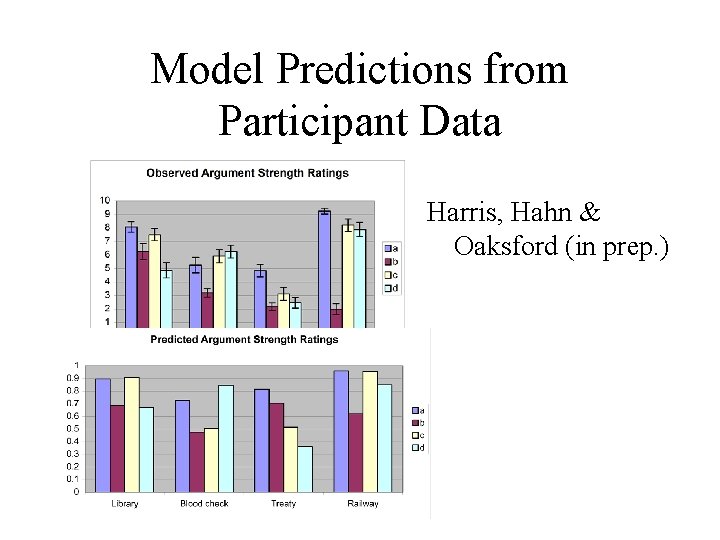
Model Predictions from Participant Data Harris, Hahn & Oaksford (in prep. )

Circularity again • God exists, because the Bible says so, and the bible is the word of God • Electrons exist because their signature effects can be seen with a particle accelerator • Both (equally) logically valid if presupposition is included as explicit premise

Circularity again • God exists, because the Bible says so, and the bible is the word of God • Electrons exist because their signature effects can be seen with a particle accelerator • Both (equally) logically valid if presupposition is included as explicit premise

Circularity: A Bayesian Perspective Shogenji (2000): probabilistic reconstruction shows some circular arguments can work: need of hypothesis in interpreting the data does not preclude data from increasing posterior belief in hypothesis Hahn & Oaksford (2006, 2007): constraint satisfaction networks, hierarchical Bayesian modelling = testable predictions about strong vs. weak circular arguments - supported by data in Hahn & Oaksford, 2007

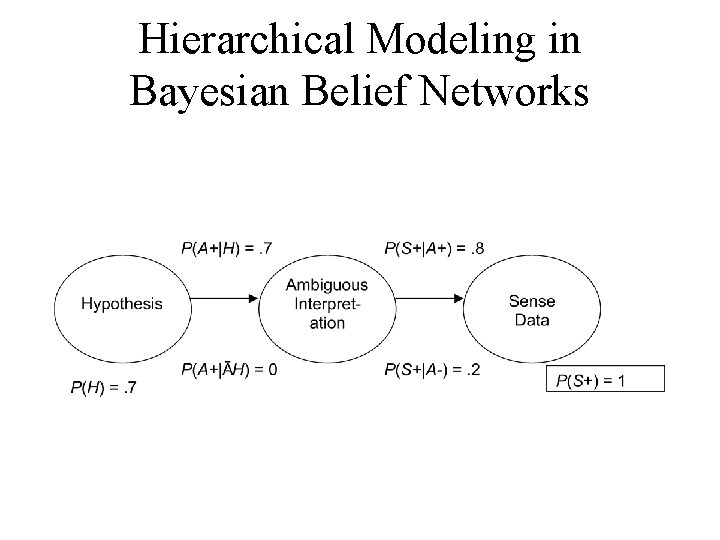
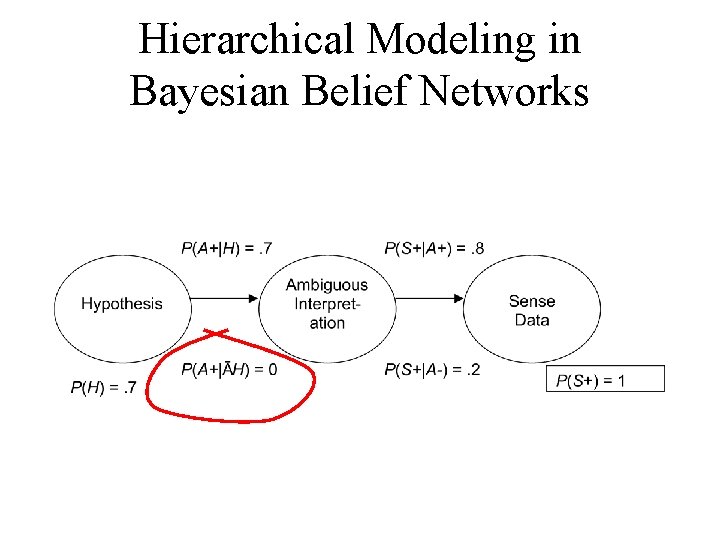
Bayesian formalization of selfdependent justification • Hierarchical Bayesian Modeling Examples contain: 1. Observation or ‘sense data’ 2. Interpretation or ‘ambiguous data’ 3. Hypothesis

Bayesian formalization of selfdependent justification • Hierarchical Bayesian Modeling Examples contain: 1. Sense data (3 cm tracks cloud chamber) 2. Ambiguous data (trace of electron) 3. Hypothesis (electron exists)

Hierarchical Modeling in Bayesian Belief Networks

Hierarchical Modeling in Bayesian Belief Networks

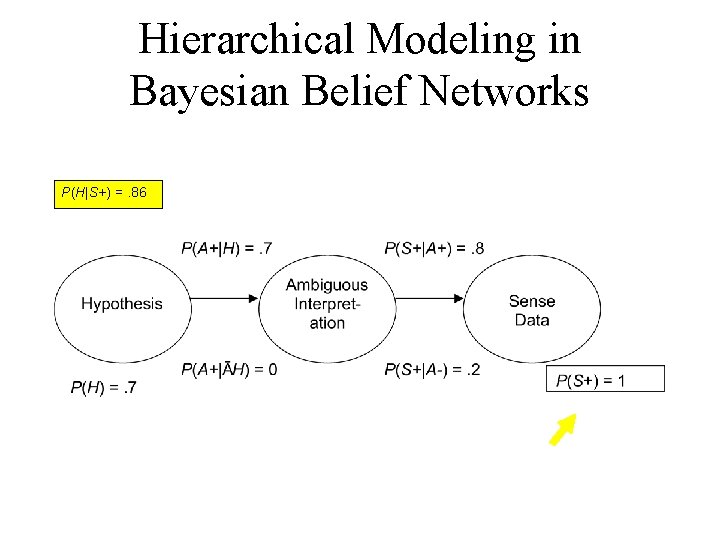
Hierarchical Modeling in Bayesian Belief Networks P(H|S+) =. 86

Slippery Slope Arguments ‘Legalizing cannabis will lead to increased heroin use’ …a kind of consequentialist argument prevalent in political, legal and moral discourse. . . involves probabilities and utilities: maximization of expected utility Experimental tests in Corner, Hahn & Oaksford, 2006

Summary • A Bayesian, normative reconstruction of core fallacies • Exp. evidence that people are sensitive to key variables determining argument strength as defined by Bayesian account • Account extends to other fallacies (Hahn & Oaksford, Synthese, 2006) • Expands to day-to-day informal reasoning/argument Bayesian analyses of scientific reasoning (e. g. , Howson & Urbach, 1989) • Bayesian probability as general, normative theory of argument strength?

Implications for Logic and Argumentation • Bayesian approach succeeds where classical logic failed because – – can deal with uncertain information capture inductive inference quantitative conditioning provides rule for dynamic updating, that is, belief revision

“Argumentation is a verbal, social, and rational activity aimed at convincing a reasonable critic of the acceptability of a standpoint by putting forward a constellation of propositions justifying or refuting the propositions expressed in the standpoint” (van Eemeren & Grootendorst, 2004, p 1) Argumentation is about (rationally) changing people’s beliefs (cf. circularity, paradoxes of material implication)

Logic & Argumentation Wealth of non-classical logics, but fallacies? Probability logic this needs to preserve key strengths – can deal with uncertain information – inductive inference – conditioning provides rule for dynamic updating, that is, belief revision that is quantitative FOProbabilistic languages such as MEBN, Bayesian Logic Programs

Leibniz “this language will be the greatest instrument of reason, ” for “when there are disputes among persons, we can simply say: Let us calculate, without further ado, and see who is right” (The Art of Discovery (1685); C, 176 (W, 51)).

Thanks to… Adam Corner Adam Harris Hatice Bayindir