EXPERIMENTS WITH LARGE GAMMA DETECTOR ARRAYS Lecture VI

EXPERIMENTS WITH LARGE GAMMA DETECTOR ARRAYS Lecture VI Ranjan Bhowmik Inter University Accelerator Centre New Delhi -110067 Lecture VI SERC-6 School March 13 - April 2, 2006

Measurement of Nuclear Moments Lecture VI SERC-6 School March 13 - April 2, 2006 2

g-Factor n n n Current loop produces a magnetic dipole moment m = i. A/c Moving charge loop has a moment m = (e/T)* pr 2/c = evr/2 c = (e/2 mc) ħ There is a similar equation for the internal charges in a proton due to its intrinsic spin Total magnetic moment contribution due to protons in a nucleus m =gl + gss Neutrons can only contribute due to the spin We have Lecture VI gl = m. N gl = 0 T gs = 5. 5857 m. N for proton gs = -3. 8256 m. N for neutron SERC-6 School March 13 - April 2, 2006 3

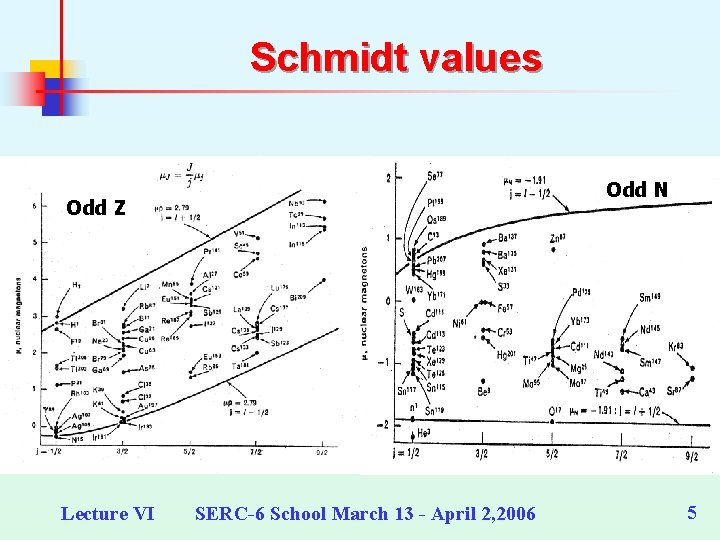
Schmidt Values The magnetic moment of a nucleus is defined as the expectation value of m along the spin direction J For a single independent nucleon this is calculated to be Substituting j = s and s =1/2 we get for j= l + 1/2 for j = l - 1/2 Lecture VI SERC-6 School March 13 - April 2, 2006 4

Schmidt values Odd N Odd Z Lecture VI SERC-6 School March 13 - April 2, 2006 5

Deviations for Schmidt Values n n n For near closed-shell nuclei deviations arise due to motion of the odd nucleon affecting the charge distribution in the core Intrinsic moments affected by nuclear medium velocity dependent spin-orbit term introduces a correction Excitation of the core : coupling to vibrational states Truncated model space in shell-model calculations The 'empirical' g-factors that reproduce the observed gfactors in s-d and f-p shell nuclei are : gs = 0. 75 gsbare glπ= 1. 1 µN glν = − 0. 1 µN NPA 694(2000)157 Lecture VI SERC-6 School March 13 - April 2, 2006 6

Deformed Nuclei n n For deformed nuclei, [Nn. Z LW] orbitals are not pure single particle wave functions but admixtures of different -values Measurement of g-factor is a sensitive test of the wave function g-factor of the levels in a band is given by : § Intrinsic g-factor is given in terms of the single particle configurations § Rotational g-factor Lecture VI SERC-6 School March 13 - April 2, 2006 7

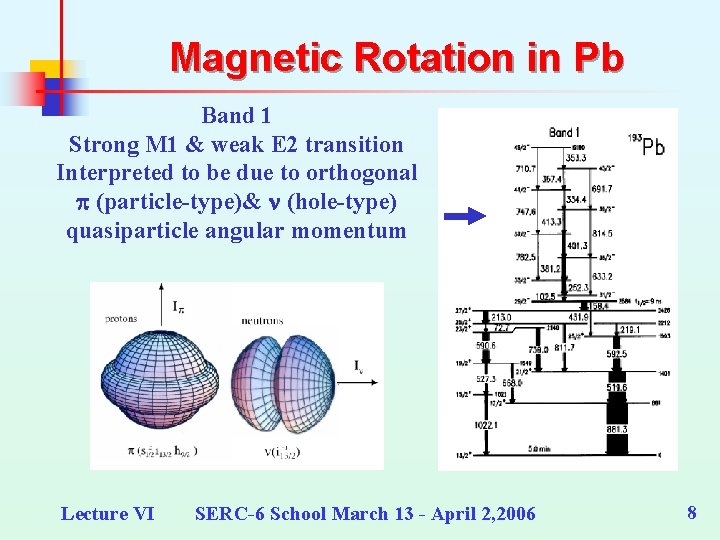
Magnetic Rotation in Pb Band 1 Strong M 1 & weak E 2 transition Interpreted to be due to orthogonal p (particle-type)& n (hole-type) quasiparticle angular momentum Lecture VI SERC-6 School March 13 - April 2, 2006 8

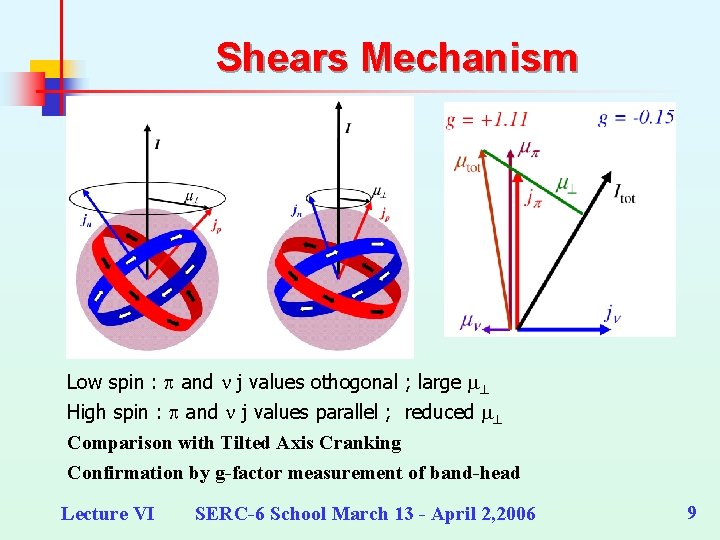
Shears Mechanism Low spin : p and n j values othogonal ; large m High spin : p and n j values parallel ; reduced m Comparison with Tilted Axis Cranking Confirmation by g-factor measurement of band-head Lecture VI SERC-6 School March 13 - April 2, 2006 9

Measurement of g-factor A nucleus with magnetic moment m will precess in an external magnetic field B with the Larmor frequency w. L In fusion reaction, the nuclear spin is preferentially oriented perpendicular to the beam direction, leading to an anisotropy in angular distribution The effect of precession of the spin in the external field is to rotate the angular distribution in time t by an angle Dq = w. Lt Level with mean life time t will rotate by Lecture VI w. L t SERC-6 School March 13 - April 2, 2006 10

Larmor Frequency n n Larmor frequency in an external magnetic field w. L=gm. NB/ħ Corresponds to a time period T=p/w = 60 ns(g/B) g in Nuclear Magneton, B in Tesla External magnetic field varies over wide range n 1 -2 Tesla iron-core electromagnet n 5 -12 Tesla superconducting solenoid n 10 -100 Tesla static field in ferromagnet n 103 -104 Tesla transient magnetic field for fast moving ions in a magnetized material Depending on the lifetime t different types of field employed Lecture VI SERC-6 School March 13 - April 2, 2006 11

Techniques for measuring g-factor Depending on the life time of the state, various methods can be employed : Life times 1 ns - 1 ms Time Differential Perturbed Angular Distribution (TDPAD) Lifetimes 1 ps – 1 ns Implantation & Perturbed Angular Correlation (IMPAC) Transient Field method Transient field with Plunger Long Lived Isomers ( ~ ms) Stroboscopy Lecture VI NMR SERC-6 School March 13 - April 2, 2006 12

TDPAD Technique n n n Stop the recoiling nuclei in a diamagnetic cubic lattice Apply external magnetic field ~ Tesla perp. To beam dir. Decay curve of the isomer by delayed coincidence or pulsed beam Put detectors at q in the reaction plane Compare the ratio of counts in +q and -q detectors Decay curve in the presence of external field where Lecture VI SERC-6 School March 13 - April 2, 2006 13

TDPAD measurement in 214 Fr n n n n produced in 208 Pb(11 B, 5 n) g-g delayed coincidence with 1068 ke. V line of 214 Fr Mean life for 11+ isomer t =148 ns External field 2. 4 T Plotted ratio R(t) R ~ ¾ a 2 sin(2 w. Lt) sin(2 q) Maximum sensitivity at q=45 NPA 567(1994)445 g = 0. 511

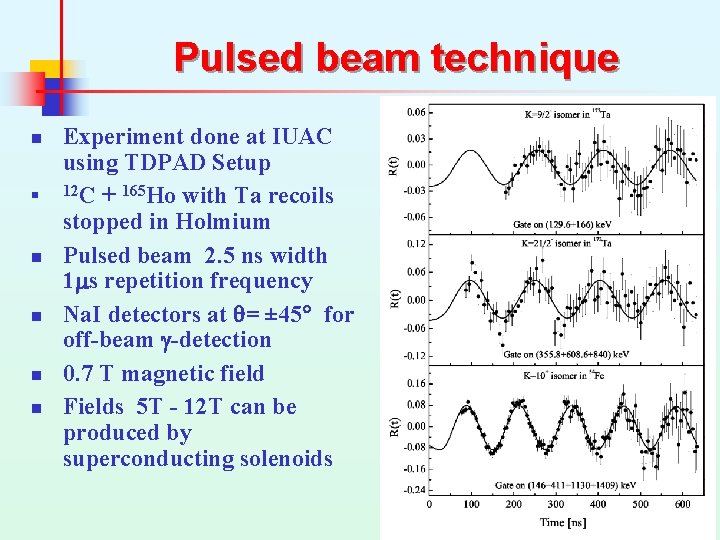
Pulsed beam technique n n n Experiment done at IUAC using TDPAD Setup 12 C + 165 Ho with Ta recoils stopped in Holmium Pulsed beam 2. 5 ns width 1 ms repetition frequency Na. I detectors at q= ± 45 for off-beam g-detection 0. 7 T magnetic field Fields 5 T - 12 T can be produced by superconducting solenoids

g-Factor measurement in 193 Pb Lecture VI SERC-6 School March 13 - April 2, 2006 16

Electric Quadrupole Moment n Strong electric field gradient In a non-cubic lattice Hyperfine splitting DE =[3 m 2 -J(J+1)]e. QVzz/[4 J(2 J-1)] Transition frequency harmonics of ħw. Q = 3 e. QVzz/[4 J(2 J-1)] Typical field gradient Vzz ~ 1018 V/cm 2 Time period ~ 20 ns for Q = 1 barn In a polycrystalline material no preferential direction Angular correlations attenuated due to hyperfine interaction n W(q, t) = 1 + S Gkk(t) ak Pk(cosq) n n n n Attenuation factor Gkk(t) = S S 2 n cos(nwt) Relative amplitude of the harmonics depend on spin J Lecture VI SERC-6 School March 13 - April 2, 2006 17

Measurement of Static Quadrupole Moment 16 O + 159 Tb with recoiling 169 Ta stopping in the target Hexagonal lattice Large electric field gradient Vzz ~ 6. 1017 V/cm 2 Na. I detectors at 0 and 90 5/2 - Attenuation factor calculated from angular anisotropy: Shows periodic structure in time dependence from which w and spin I can be calculated Lecture VI SERC-6 School March 13 - April 2, 2006 18

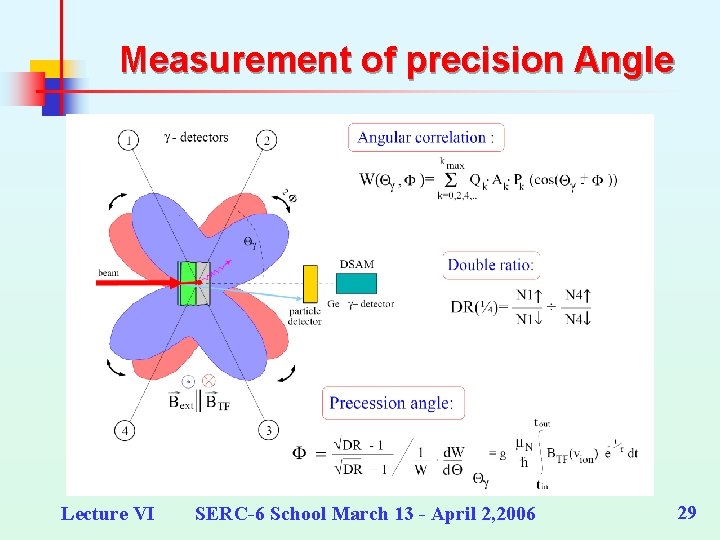
Extension to short lifetimes n n For short lifetimes, not possible to measure the entire wt cycle Periodically switch the magnetic field 'up' and 'down' Put detectors at q and preferably also at p q To measure the field up-down counting asymmetry and systematic error, get Double ratio r where & are the counts in 'field up' and 'field down' position § Another ratio r 4 is which corrects for beam spot change Lecture VI SERC-6 School March 13 - April 2, 2006 19

Small Precision Angle n Small rotation Dq < 100 mrad n Precession angle given by Dq n n where e =(1+r)/(1 -r) S is the logarithmic derivative of angular distribution n S is maximum at q ~ 45 in fusion reaction n g-factor estimated from g = w ħ /Bm. N = (Dq. ħ)/t. Bm. N n For Coulomb Excitation W(q) ~ Z 20 = sin 2 q cos 2 q S Maximum at 22. 5 , 67. 5 Lifetime t must be known Lecture VI SERC-6 School March 13 - April 2, 2006 20

IMPAC Technique n n n Energetic recoils implanted in a ferromagnetic host Large internal magnetic field ~ 30 - 100 T Static field can be aligned by applying a small external magnetic field ~ 0. 01 – 0. 1 T perpendicular to beam direction Rotation Dq can be measured either by angular distribution or by angular correlation Corrections required for transient field and feeding delay Corrections small if lifetime large compared to feeding time and stopping time Lecture VI SERC-6 School March 13 - April 2, 2006 21

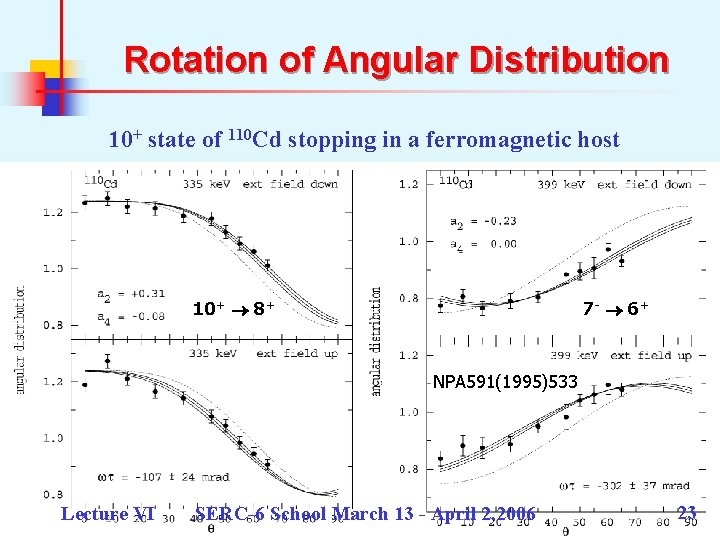
g-factor measurement in 110 Cd n n n n n 110 Cd populated in 13 C + 100 Mo reaction Target evaporated on a 4 mg/cm 2 Gd foil cooled to LN 2 External field of 0. 05 T to polarize internal field Field reversed every 15 min Lifetime of 10+ level ~ 800 ps >> stopping time (~ 2 ps) Feeding and transient field corrections neglected Static hyperfine field in Gd ~ 30 T at 92 K From the shift in angular distribution in ‘field up’ & ‘field down’ conditions, precession angle calculated 7 - level ( t ~ 1 ns) fed from 10+ level, large feeding correction Lecture VI SERC-6 School March 13 - April 2, 2006 22

Rotation of Angular Distribution 10+ state of 110 Cd stopping in a ferromagnetic host 10+ 8+ 7 - 6 + NPA 591(1995)533 Lecture VI SERC-6 School March 13 - April 2, 2006 23

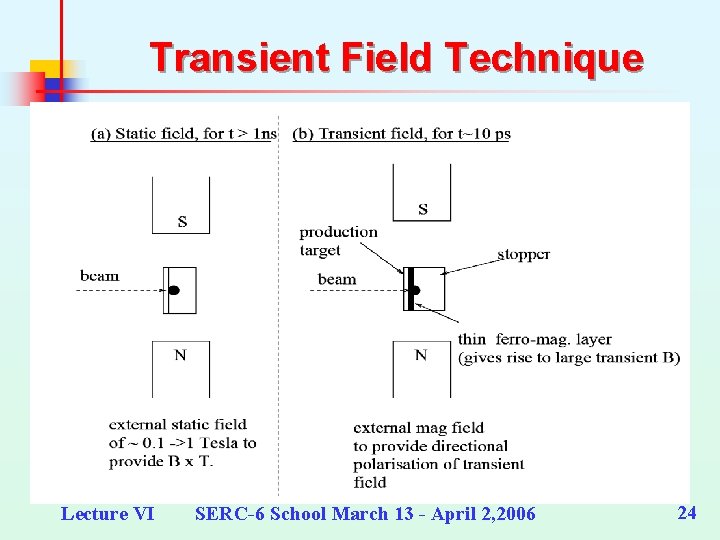
Transient Field Technique Lecture VI SERC-6 School March 13 - April 2, 2006 24

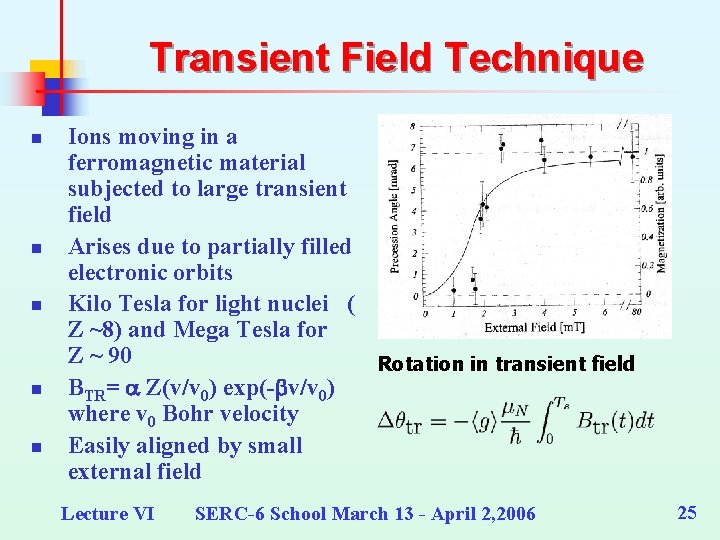
Transient Field Technique n n n Ions moving in a ferromagnetic material subjected to large transient field Arises due to partially filled electronic orbits Kilo Tesla for light nuclei ( Z ~8) and Mega Tesla for Z ~ 90 Rotation in transient field BTR= a Z(v/v 0) exp(-bv/v 0) where v 0 Bohr velocity Easily aligned by small external field Lecture VI SERC-6 School March 13 - April 2, 2006 25

Transient Field Method Direct feeding of low spin levels in Coulomb Excitation B field Magnetisation Target recoil Beam In Ferromagnetic layer B field direction is set Coulex Recoil Nuclear spin Target Ferromagnetic Layer Lecture VI Stopper Recoiling Coulex nuclear spins aligned perp. to beam Precess about B field Angular distribution of decay gamma emission rotated SERC-6 School March 13 - April 2, 2006 26

g-factor in Inverse Kinematics Lecture VI SERC-6 School March 13 - April 2, 2006 27

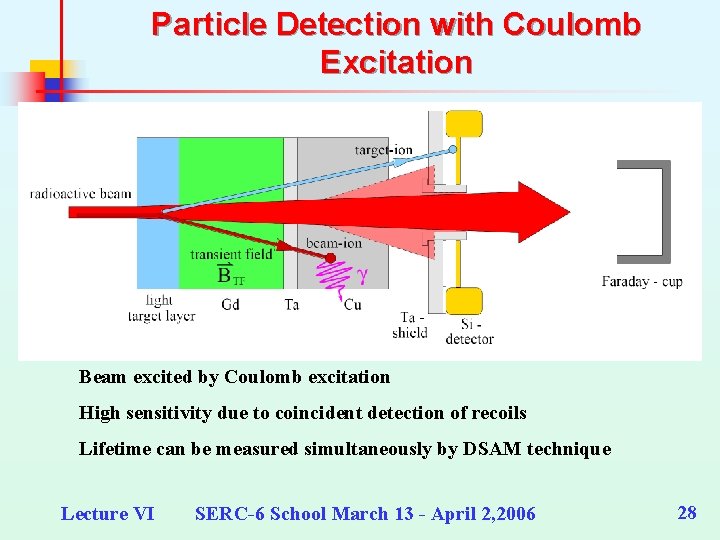
Particle Detection with Coulomb Excitation Beam excited by Coulomb excitation High sensitivity due to coincident detection of recoils Lifetime can be measured simultaneously by DSAM technique Lecture VI SERC-6 School March 13 - April 2, 2006 28

Measurement of precision Angle Lecture VI SERC-6 School March 13 - April 2, 2006 29

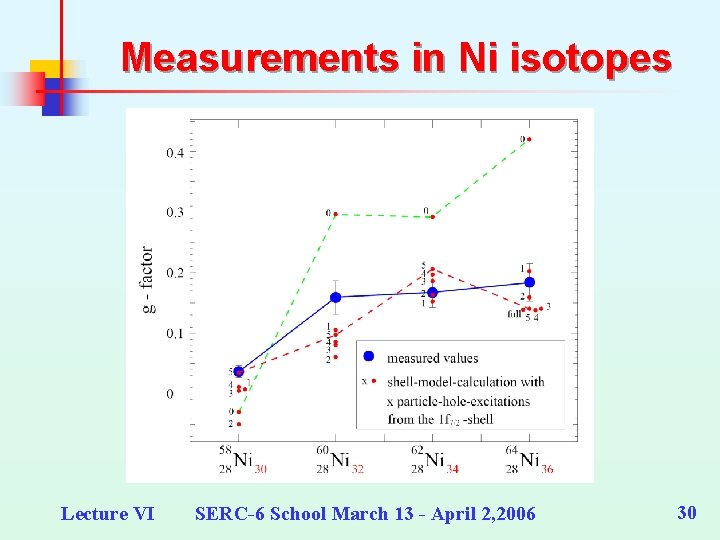
Measurements in Ni isotopes Lecture VI SERC-6 School March 13 - April 2, 2006 30

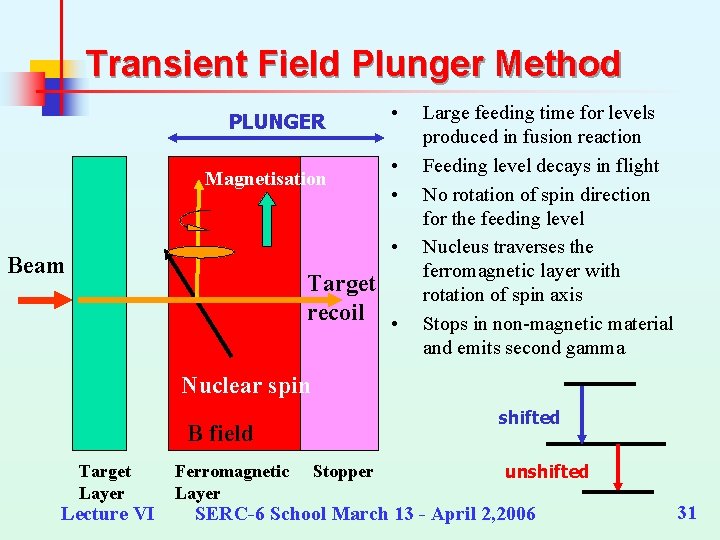
Transient Field Plunger Method PLUNGER • Magnetisation • • • Beam Target recoil • Large feeding time for levels produced in fusion reaction Feeding level decays in flight No rotation of spin direction for the feeding level Nucleus traverses the ferromagnetic layer with rotation of spin axis Stops in non-magnetic material and emits second gamma Nuclear spin shifted B field Target Layer Lecture VI Ferromagnetic Layer Stopper unshifted SERC-6 School March 13 - April 2, 2006 31

Lecture VI SERC-6 School March 13 - April 2, 2006 32