EXPERIMENTO FACTORIAL 23 En este modelo factorial particular

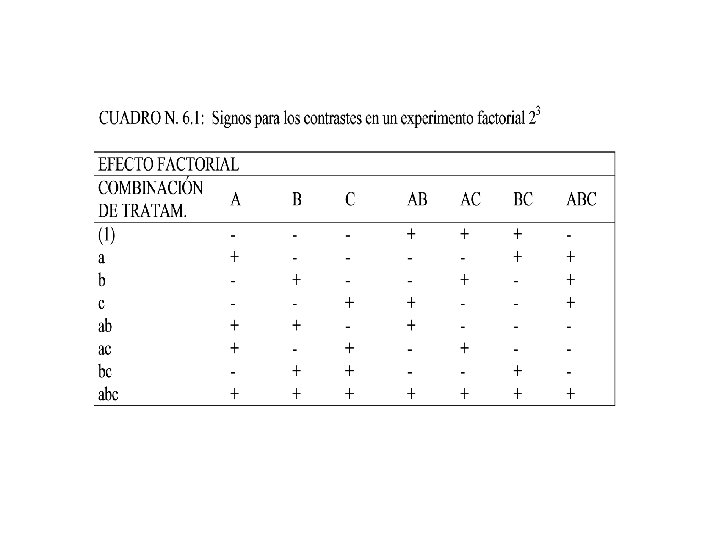
EXPERIMENTO FACTORIAL 23 En este modelo factorial particular existen 3 factores A, B, C cada uno con dos niveles y con 8 combinaciones de tratamientos: (1), a, b, c, ab, ac, bc, abc. Las combinaciones de tratamientos y los signos algebraicos apropiados para contraste utilizados en el cálculo de las sumas de cuadrado para los efectos principales y de interacción, se presenta en el siguiente cuadro:

• De acuerdo al cuadro 4. 1 se puede determinar la suma de cuadrados para el efecto del contraste A : • Suma de cuadrados para el contraste B

Suma del cuadrado de contrastes de C Suma del cuadrado de contrastes AB Suma del cuadrado de contrastes de AC

• Suma de cuadrados para el contraste BC Suma de cuadrados para el contraste ABC Para un experimento factorial 2^k las sumas de cuadrados con único grado de libertad para los efectos principales y de interacción se obtienen elevando al cuadrado los contrastes apropiados en los totales de los tratamientos y dividiendo entre (2^k)(n), donde n es el numero de repeticiones de las combinaciones de tratamientos.

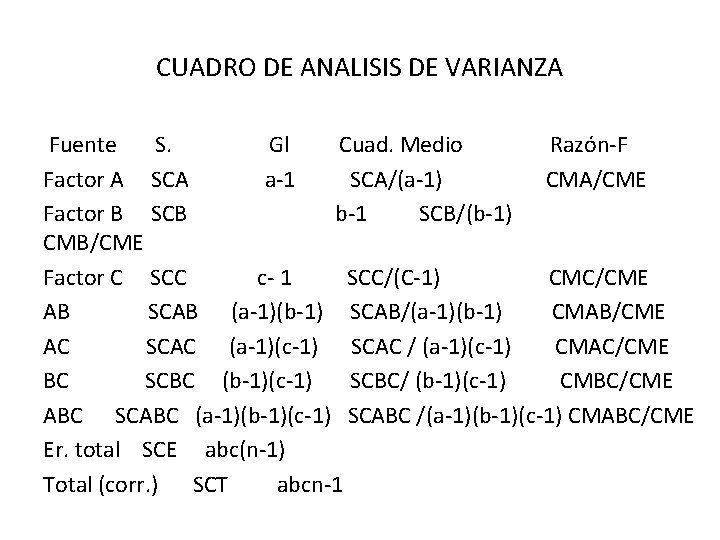
CUADRO DE ANALISIS DE VARIANZA Fuente S. Gl Cuad. Medio Razón-F Factor A SCA a-1 SCA/(a-1) CMA/CME Factor B SCB b-1 SCB/(b-1) CMB/CME Factor C SCC c- 1 SCC/(C-1) CMC/CME AB SCAB (a-1)(b-1) SCAB/(a-1)(b-1) CMAB/CME AC SCAC (a-1)(c-1) SCAC / (a-1)(c-1) CMAC/CME BC SCBC (b-1)(c-1) SCBC/ (b-1)(c-1) CMBC/CME ABC SCABC (a-1)(b-1)(c-1) SCABC /(a-1)(b-1)(c-1) CMABC/CME Er. total SCE abc(n-1) Total (corr. ) SCT abcn-1

Ejemplo • Se presenta un estudio de efecto que tiene el porcentaje de conservantes 10 y 12% , la temperatura a - 20 y -10 y la rapidez en el volumen a 200 y 250 sobre la línea de envasado de yogur, suponga que se usa solo dos niveles de porcentaje de conservantes , dos niveles de conservantes y el volumen de rapidez también a dos niveles los datos se dan a continuaqciaon :

CUADRO No. 6. 2 • _________________ • Temperatura (B) • 200 250 • Rapidez (C) • 1 2 % (A) C 10 -1 -1 -1 1 o -1 0 0 1 s 12 0 2 2 6 v. 1 1 3 5 ________________

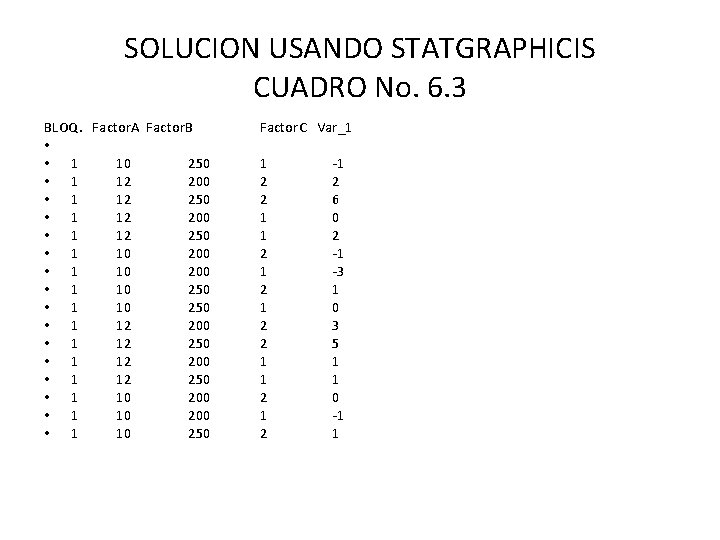
SOLUCION USANDO STATGRAPHICIS CUADRO No. 6. 3 BLOQ. Factor. A Factor. B • • 1 10 250 • 1 12 200 • 1 12 250 • 1 10 200 • 1 10 250 Factor. C Var_1 1 2 2 1 1 2 1 2 -1 2 6 0 2 -1 -3 1 0 3 5 1 1 0 -1 1

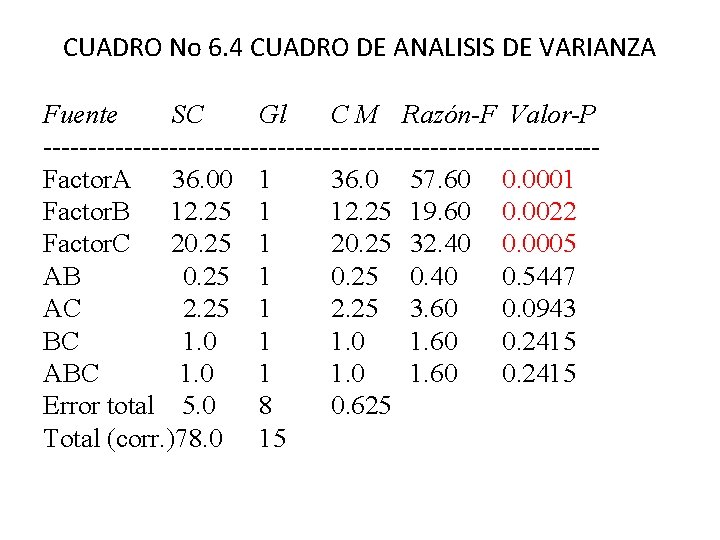
CUADRO No 6. 4 CUADRO DE ANALISIS DE VARIANZA Fuente SC Gl C M Razón-F Valor-P -------------------------------Factor. A 36. 00 1 36. 0 57. 60 0. 0001 Factor. B 12. 25 19. 60 0. 0022 Factor. C 20. 25 1 20. 25 32. 40 0. 0005 AB 0. 25 1 0. 25 0. 40 0. 5447 AC 2. 25 1 2. 25 3. 60 0. 0943 BC 1. 0 1. 60 0. 2415 ABC 1. 0 1. 60 0. 2415 Error total 5. 0 8 0. 625 Total (corr. )78. 0 15

TECNICA DE YATES PARA EL CALCULO DE CONTRASTES Yates invento una técnica sistemática para obtener los efectos factoriales. Las combinaciones de tratamientos y las observaciones deben escribirse en forma estándar. Para un factor la forma estándar será (1). a. Para dos factores se agregan (1), a, b y ab, obtenidas de multiplicar las primeras combinaciones de tratamientos por la letra b. Para tres factores será entonces: (1), a, b, c, ab, ac, bc, abc.

METODOLOGIA • Se colocan las combinaciones de tratamientos y los resultados totales correspondientes en una columna en su orden estándar. • Se desarrolla la mitad superior de una columna marcada con (1) sumando los dos primeros resultados después los siguientes dos y así sucesivamente. La mitad inferior se obtiene restando el primero al segundo de cada uno de estos factores pares. • Se repite la operación usando los resultados de la columna (1) para obtener la columna (2). Esta operación se repite hasta la k columna para un experimento factorial 2 a la k

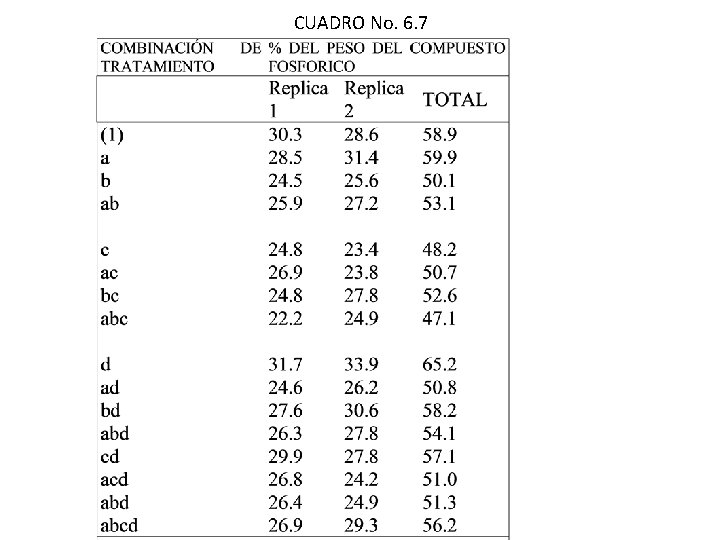
EJEMPLO En un experimento de laboratorio se desea probar el efecto de 4 factores y su interacción sobre la concentración (porcentaje del peso) de cierto compuesto fosfórico en materiales fundidos. Las variables son: (A), porcentaje de fosforo en la refinación; (B), porcentaje de material fundido; (C), tiempo de derretimiento y (D), tiempo de retención. Los 4 factores se varían en un experimento factorial 24 tomando dos muestra y midiendo su contenido en cada combinación de tratamientos. Efectué el análisis de varianza mediante la técnica de YATES.

• El primer valor de la k-ésima columna será el gran total de resultados, en el experimento. Cada uno de los restantes será un contraste en los totales de los tratamientos. Finalmente, la suma de cuadrados para los efectos principales y de interacción se obtienen elevando al cuadrado los valores de la columna (k) y dividiéndolos entre (2 k)(n), donde, n es el numero de replicas y 2 k la suma de cuadrados de los coeficientes de los contrastes individuales.

CUADRO No. 6. 7

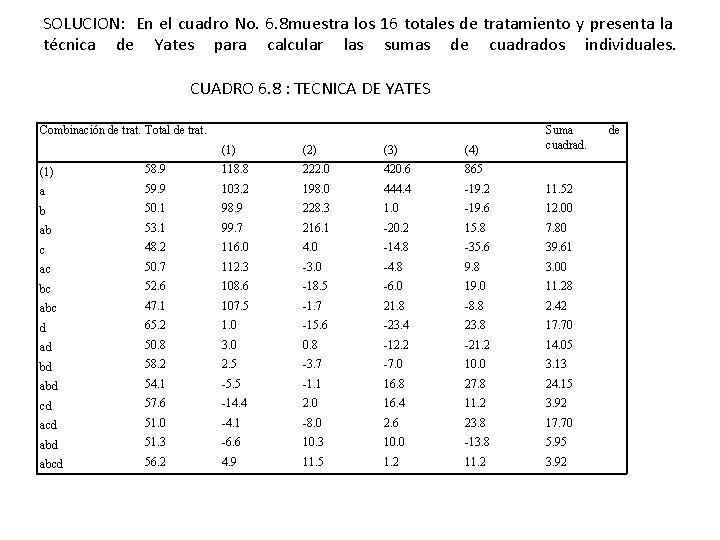
SOLUCION: En el cuadro No. 6. 8 muestra los 16 totales de tratamiento y presenta la técnica de Yates para calcular las sumas de cuadrados individuales. CUADRO 6. 8 : TECNICA DE YATES Combinación de trat. Total de trat. (1) (2) (3) (4) Suma cuadrad. (1) 58. 9 118. 8 222. 0 420. 6 865 a 59. 9 103. 2 198. 0 444. 4 -19. 2 11. 52 b 50. 1 98. 9 228. 3 1. 0 -19. 6 12. 00 ab 53. 1 99. 7 216. 1 -20. 2 15. 8 7. 80 c 48. 2 116. 0 4. 0 -14. 8 -35. 6 39. 61 ac 50. 7 112. 3 -3. 0 -4. 8 9. 8 3. 00 bc 52. 6 108. 6 -18. 5 -6. 0 19. 0 11. 28 abc 47. 1 107. 5 -1. 7 21. 8 -8. 8 2. 42 d 65. 2 1. 0 -15. 6 -23. 4 23. 8 17. 70 ad 50. 8 3. 0 0. 8 -12. 2 -21. 2 14. 05 bd 58. 2 2. 5 -3. 7 -7. 0 10. 0 3. 13 abd 54. 1 -5. 5 -1. 1 16. 8 27. 8 24. 15 cd 57. 6 -14. 4 2. 0 16. 4 11. 2 3. 92 acd 51. 0 -4. 1 -8. 0 2. 6 23. 8 17. 70 abd 51. 3 -6. 6 10. 3 10. 0 -13. 8 5. 95 abcd 56. 2 4. 9 11. 5 1. 2 11. 2 3. 92 de

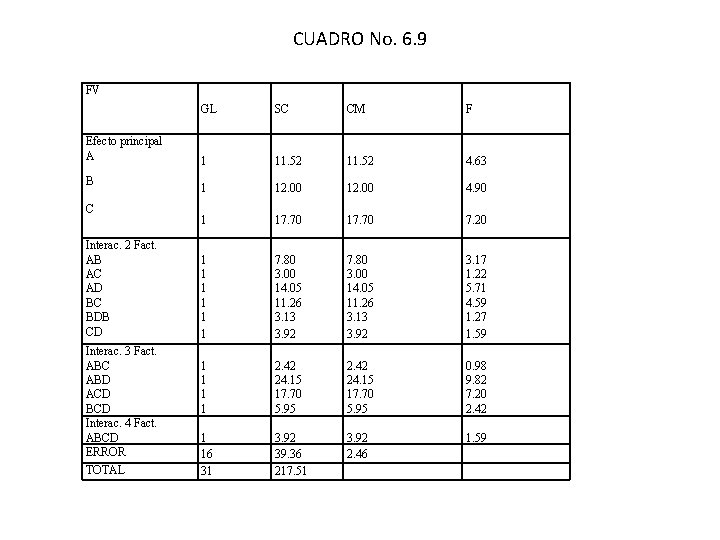
SUMA DE CUADRADOS La suma de cuadrados del total esta dado por : Ahora se puede iniciar el análisis de varianza como se indica en el cuadro No 6. 9 nótese que las interacciones AD, BC, ABD y ACD son significativas cuando se comparan con F(0. 05)(1, 16)=4. 49. las pruebas sobre los efectos principales (los que, en presencia de interacciones, pueden considerarse los efectos promedios sobre los niveles de otros factores) indican significancia de cada caso.

Con frecuencia el investigador ya sabe que ciertas interacciones en un experimento factorial 2 k son significantes y que no deben figurar en el modelo. Por ejemplo, en un experimento factorial 24 se puede postular un modelo que contenga solamente los efectos de interacciones de dos factores y después funcionar la suma de cuadrados y los correspondientes grados de libertad de las restantes interacciones de alto orden con error puro. Esto se hace en la practica en lugar de tomar varias replicas.

CUADRO No. 6. 9 FV Efecto principal A B C Interac. 2 Fact. AB AC AD BC BDB CD Interac. 3 Fact. ABC ABD ACD BCD Interac. 4 Fact. ABCD ERROR TOTAL GL SC CM F 1 11. 52 4. 63 1 12. 00 4. 90 1 17. 70 7. 20 1 1 1 1 16 31 7. 80 3. 00 14. 05 11. 26 3. 13 3. 92 2. 42 24. 15 17. 70 5. 95 3. 92 39. 36 217. 51 7. 80 3. 00 14. 05 11. 26 3. 13 3. 92 2. 42 24. 15 17. 70 5. 95 3. 92 2. 46 3. 17 1. 22 5. 71 4. 59 1. 27 1. 59 0. 98 9. 82 7. 20 2. 42 1. 59

PRACTICA No. 6 THE END