Experimental Verification of the Fluctuation Theorem in ExpansionCompression

Experimental Verification of the Fluctuation Theorem in Expansion/Compression Processes of a Single-Particle Gas Lee Dong-yun¹, Chulan Kwon², Hyuk Kyu Pak¹ Department of physics, Pusan National University, Korea¹ Department of physics, Myongji University, Korea² Nonequilibrium Statistical Physics of Complex Systems, KIAS, July 8, 2014

BIO-SOFT MATTER PHYSICS LAB Ph. D studnt: Dong Yun Lee Collaborator: Chulan Kwon Page 2

Outline Introduction Experiment Results Page 3

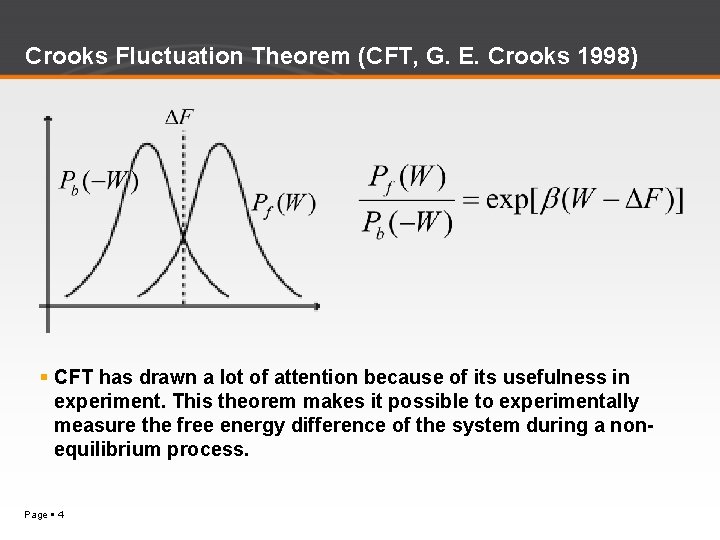
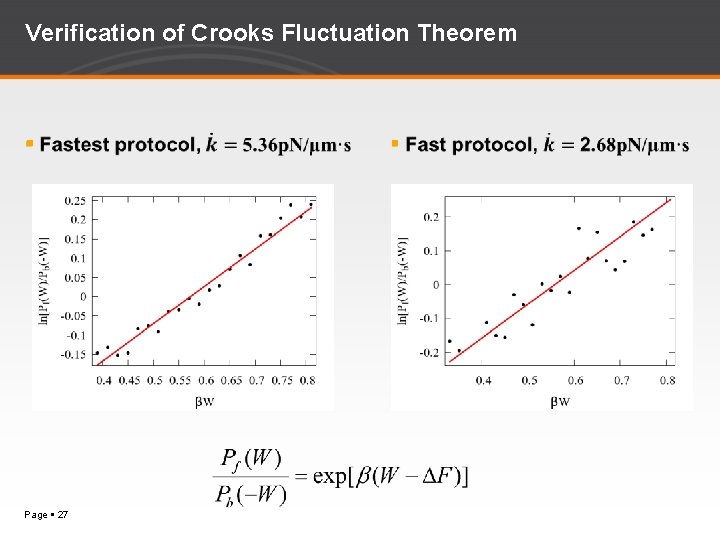
Crooks Fluctuation Theorem (CFT, G. E. Crooks 1998) CFT has drawn a lot of attention because of its usefulness in experiment. This theorem makes it possible to experimentally measure the free energy difference of the system during a nonequilibrium process. Page 4

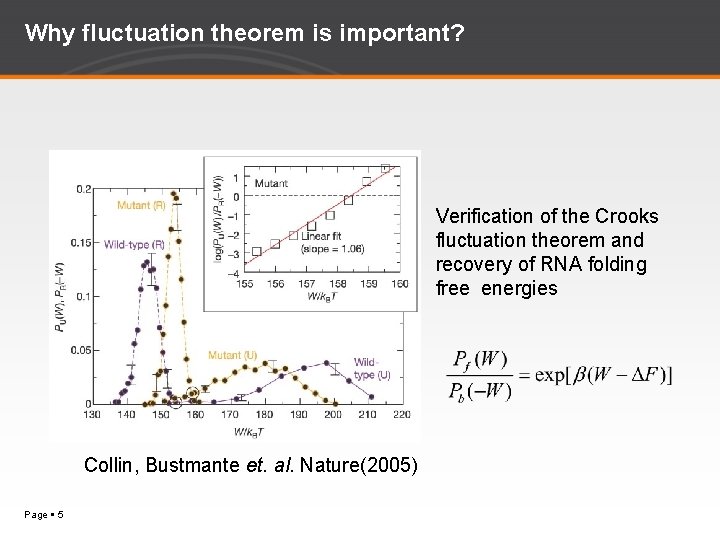
Why fluctuation theorem is important? Verification of the Crooks fluctuation theorem and recovery of RNA folding free energies Collin, Bustmante et. al. Nature(2005) Page 5

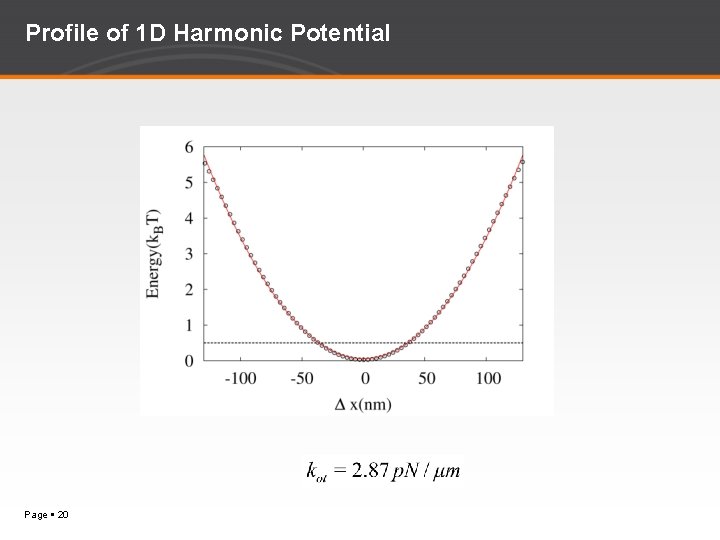
Idea Consider a particle trapped in a 1 D harmonic potential where is a trap strength of the potential. When the trap strength is either increasing or decreasing isothermally in time, the particle is driven from equilibrium. Since the size of the system is finite, one can test the fluctuation theorems in this system. We measure the work distribution and determine the free energy difference of the process by using Crooks fluctuation theorem. Page 6

Free Energy Difference of the System Harmonic oscillator (in 1 D) forward - Hamiltonian is given by backward - Partition function is - Free energy difference between two equilibrium states at the same temperature is - Forward process : , Backward process: - During these processes: Page 7

1 D Brownian Motion of Single Particle in Heat Bath Page 8 Thermodynamic 1 st Law

1 D Brownian Motion of Single Particle in Heat Bath Thermodynamic 1 st Law In equilibrium, In non-equilibrium steady state, Page 9

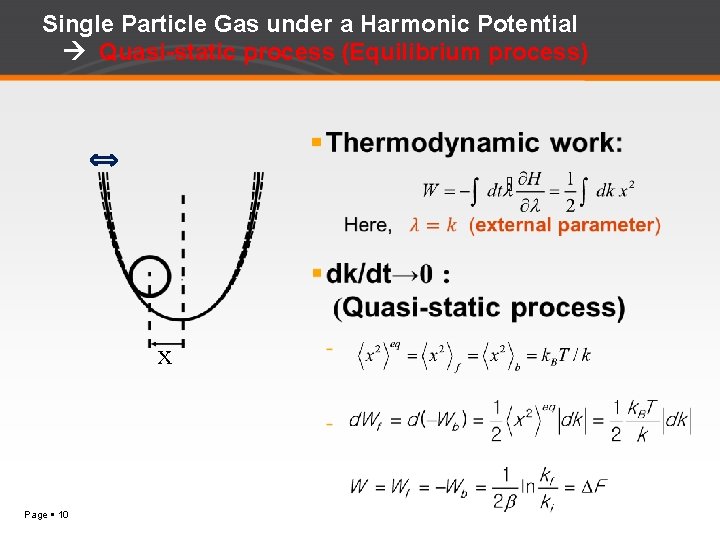
Single Particle Gas under a Harmonic Potential Quasi-static process (Equilibrium process) x Page 10

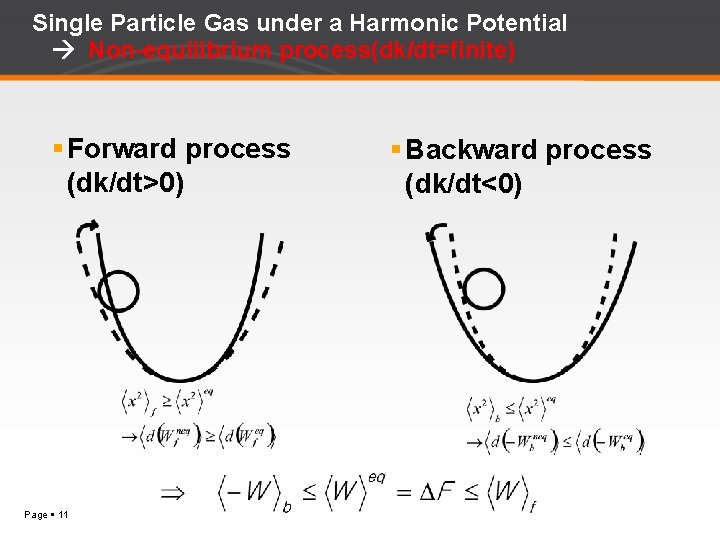
Single Particle Gas under a Harmonic Potential Non-equilibrium process(dk/dt=finite) Forward process (dk/dt>0) Page 11 Backward process (dk/dt<0)

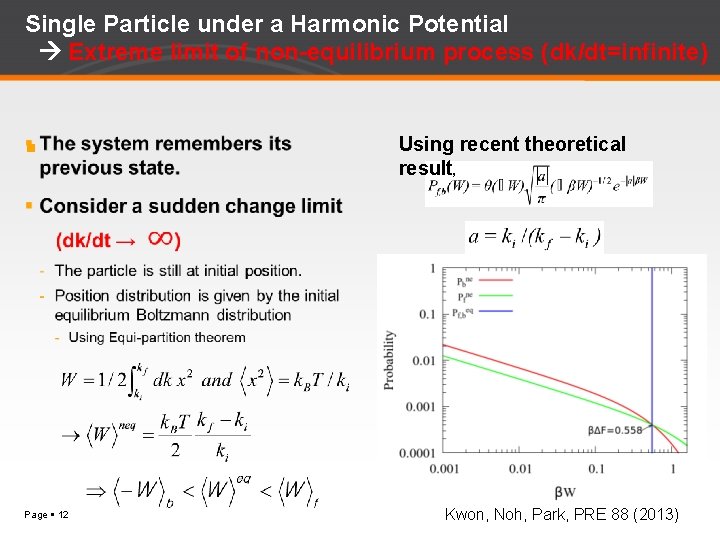
Single Particle under a Harmonic Potential Extreme limit of non-equilibrium process (dk/dt=infinite) Page 12 Using recent theoretical result, Kwon, Noh, Park, PRE 88 (2013)

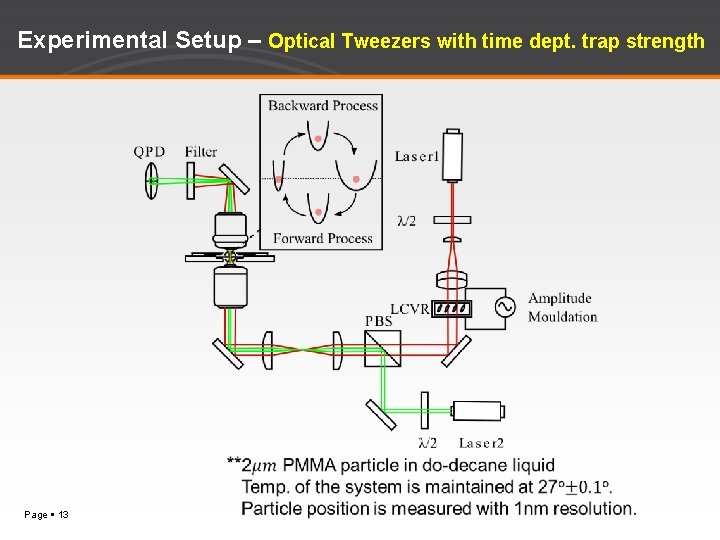
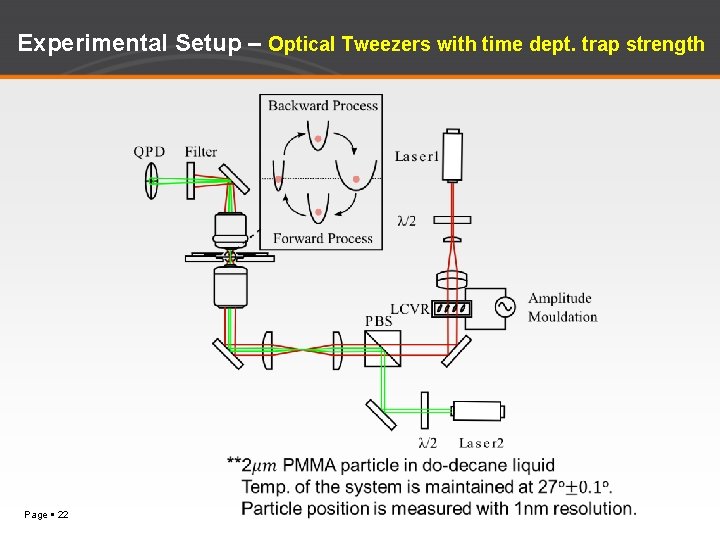
Experimental Setup – Optical Tweezers with time dept. trap strength Page 13

Optical Tweezers Developed by A. Ashkin By strongly focusing a laser beam, one can create a large electric field gradient which can create a force on a colloidal particle with a radial displacement from the center of the trap. Potential Energy For small displacements the force is a Hooke’s law force. O Page 14

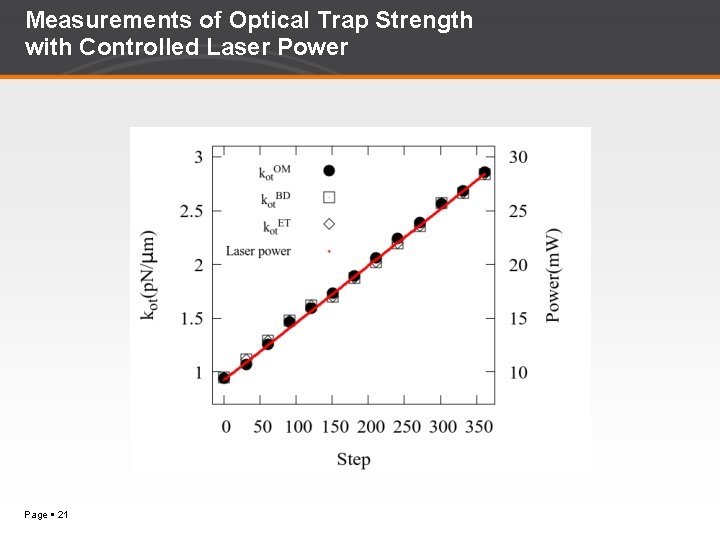
Control of the Trap Strength The optical trap strength is proportional to the laser power. Therefore, when the laser power is changed linearly in time, the optical strength should be increased or decreased linearly in time. The laser power is controlled using LCVR(Liquid Crystal Variable Retarders) which allows manipulation of polarization states by applying an electric field to the liquid crystal. Page 15

Laser Power Stability Since the optical trap strength is proportional to the laser power, it is important to have a stable laser power in time. A feedback control of the laser power is used to reduce the long time fluctuation of the laser power. During the experiment, the fluctuation of laser power is less than ± 0. 5%. Page 16

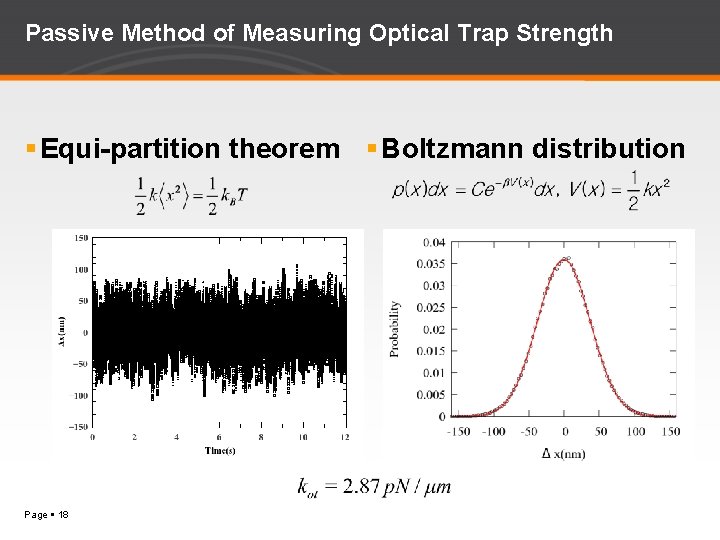
Measurements of Optical Trap Strength The optical trap strength is calibrated with three different methods - Equi-partition theorem - Boltzmann distribution method - Oscillating optical tweezers method Page 17

Passive Method of Measuring Optical Trap Strength Equi-partition theorem Boltzmann distribution Page 18

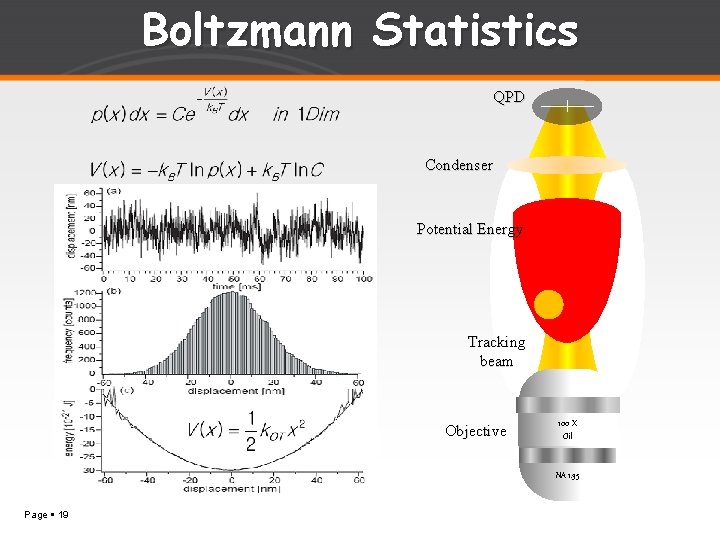
Boltzmann Statistics QPD Condenser Potential Energy Tracking beam Objective 100 X Oil NA 1. 35 Page 19

Profile of 1 D Harmonic Potential Page 20

Measurements of Optical Trap Strength with Controlled Laser Power Page 21

Experimental Setup – Optical Tweezers with time dept. trap strength Page 22

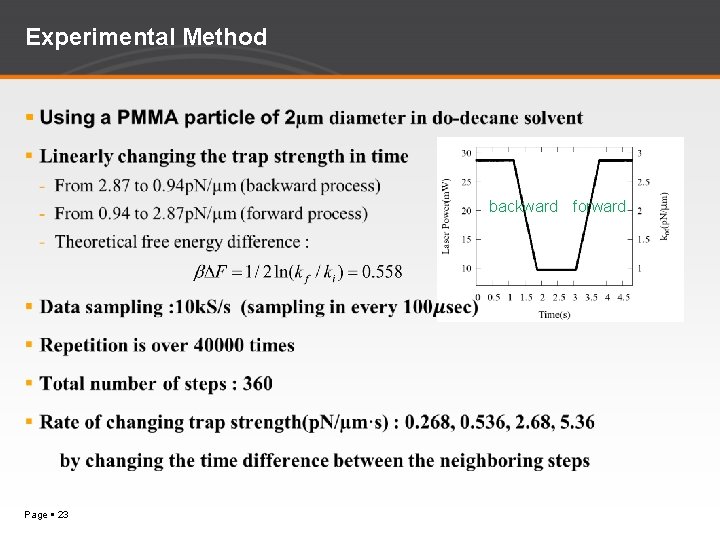
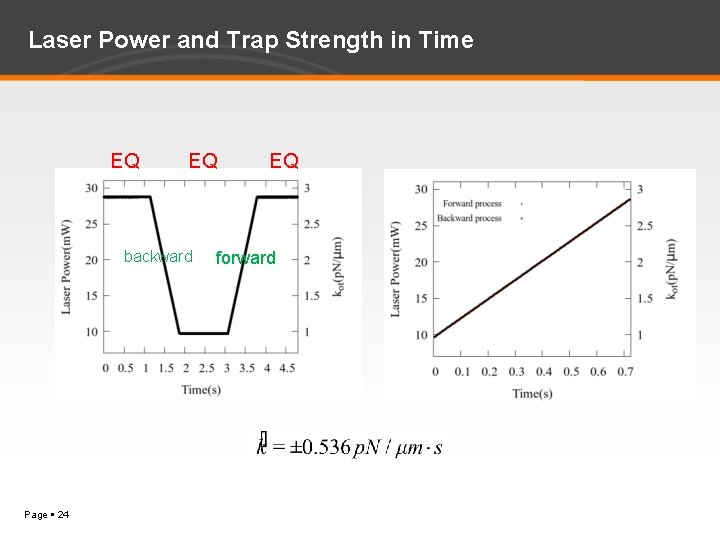
Experimental Method backward forward Page 23

Laser Power and Trap Strength in Time EQ EQ backward Page 24 EQ forward

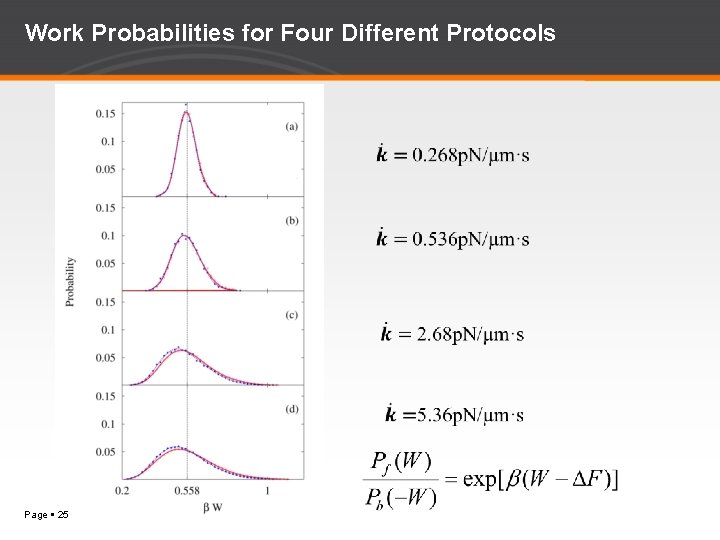
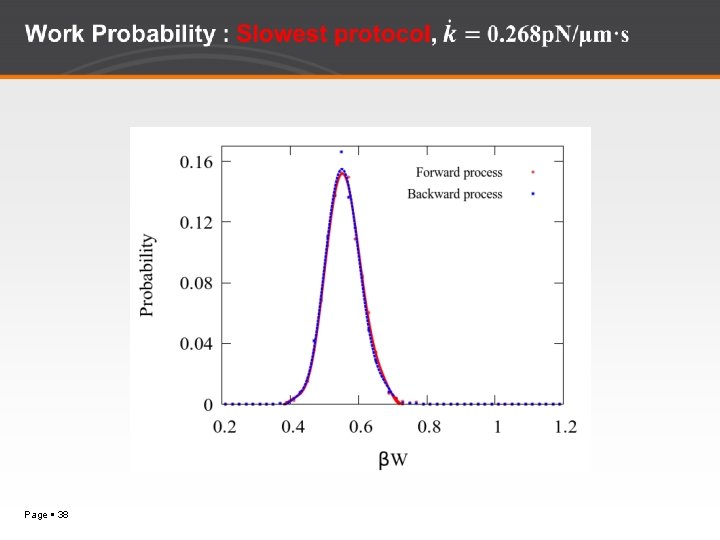
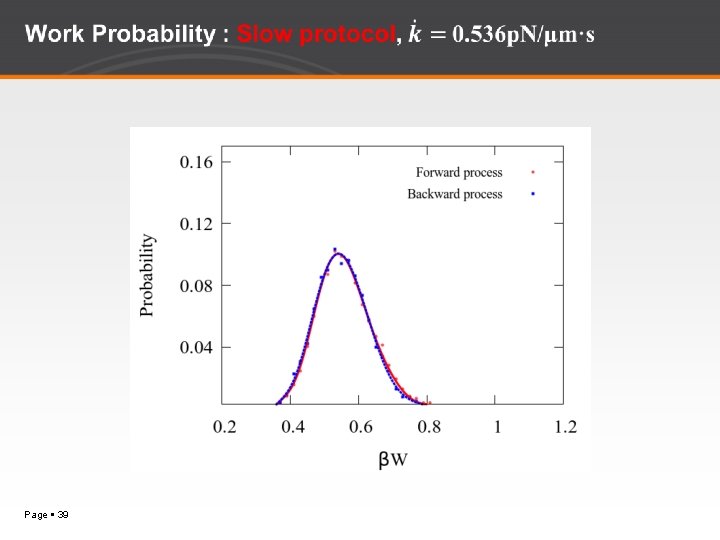
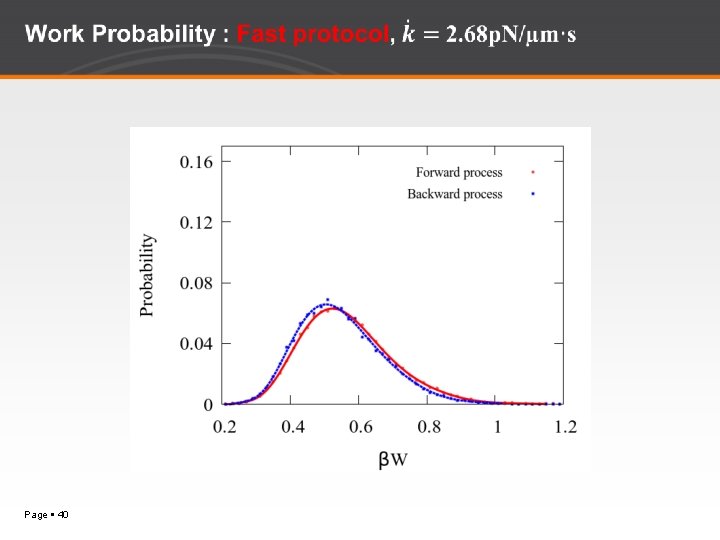
Work Probabilities for Four Different Protocols Page 25

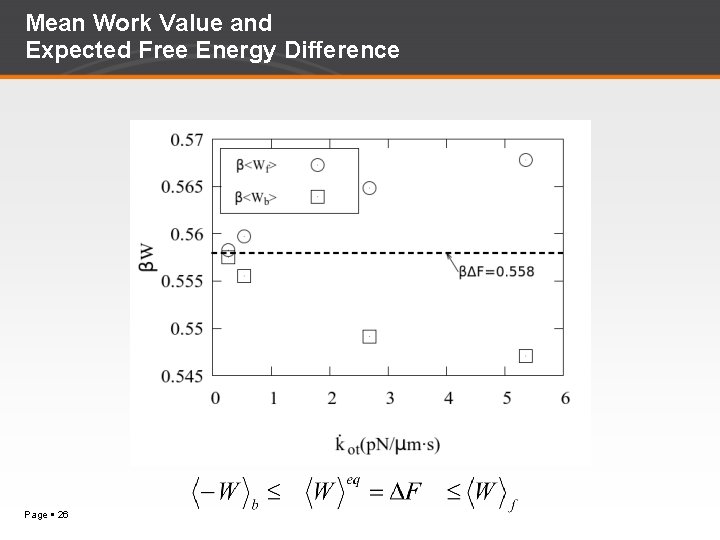
Mean Work Value and Expected Free Energy Difference Page 26

Verification of Crooks Fluctuation Theorem Page 27

Conclusion We experimentally demonstrated the CFT in an exactly solvable real system. We also showed that mean works obey in non-equilibrium processes. Useful to make a micrometer-sized stochastic heat engine. Page 28

Thank you for your attentions. Page

Supplement

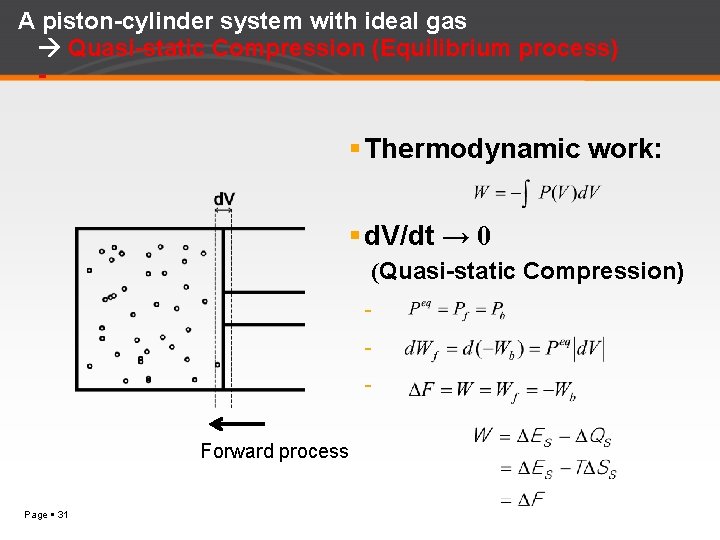
A piston-cylinder system with ideal gas Quasi-static Compression (Equilibrium process) - Thermodynamic work: d. V/dt → 0 (Quasi-static Compression) Forward process Page 31

A piston-cylinder system with ideal gas Non-equilibrium process (d. V/dt= finite) - Backward process (Expansion d. V/dt>0) Page 32 Forward process (Compression d. V/dt<0)

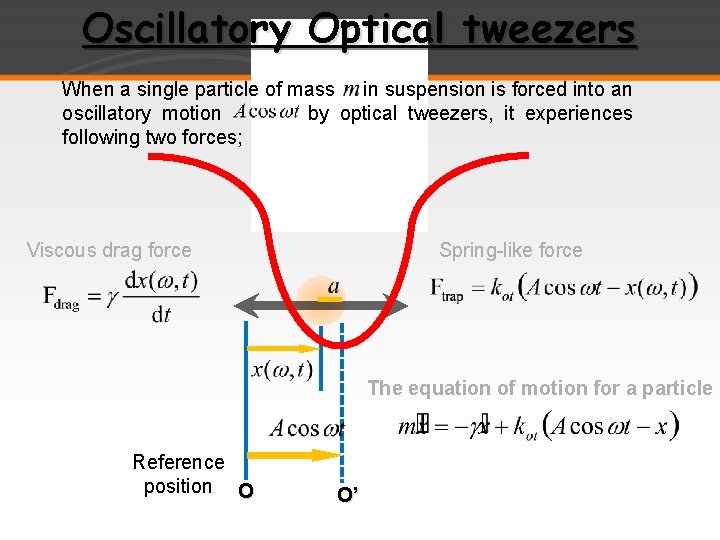
Oscillatory Optical tweezers When a single particle of mass in suspension is forced into an oscillatory motion by optical tweezers, it experiences following two forces; Viscous drag force Spring-like force The equation of motion for a particle Reference position O O’

Oscillatory Optical tweezers The equation of motion for a particle trapped by an oscillating trap in a viscous medium, as a function of Neglect the first term ( ) (In extremely overdamped case ), and assume a steady state solution in the form The amplitude and the phase of the displacement of a trapped particle is given by where the amplitude (D(ω)) and the phase shift (δ(ω)) can be measured directly with a lock-in amplifier and set-up of the oscillatory optical tweezers in the next page, .

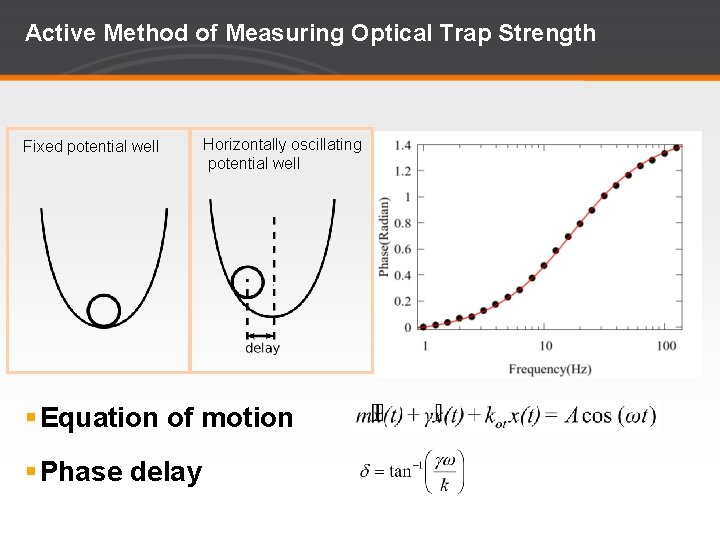
Active Method of Measuring Optical Trap Strength Fixed potential well Horizontally oscillating potential well Equation of motion Phase delay

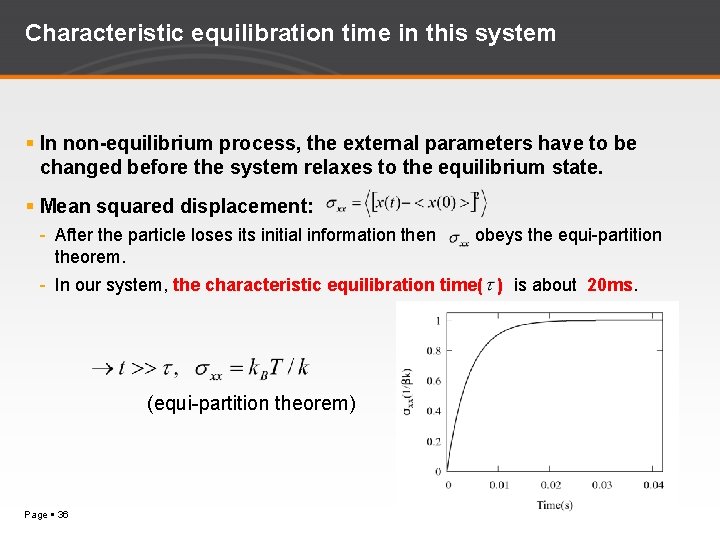
Characteristic equilibration time in this system In non-equilibrium process, the external parameters have to be changed before the system relaxes to the equilibrium state. Mean squared displacement: - After the particle loses its initial information then obeys the equi-partition theorem. - In our system, the characteristic equilibration time( ) is about 20 ms. (equi-partition theorem) Page 36

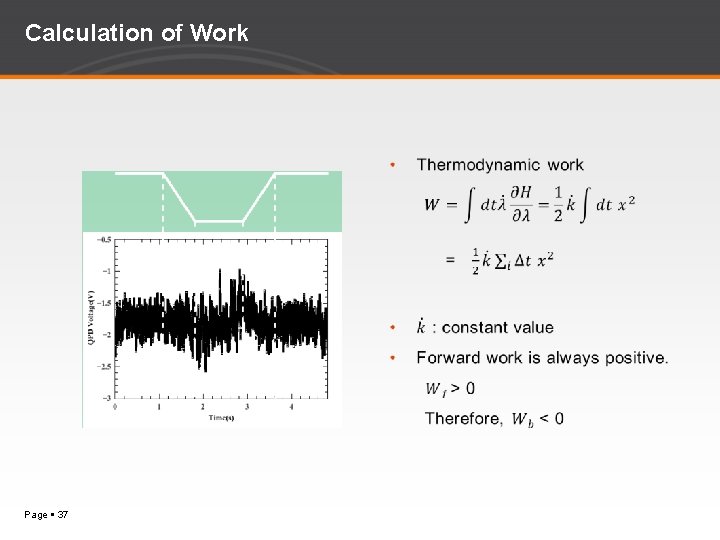
Calculation of Work Page 37

Page 38

Page 39

Page 40

Page 41