Experimental techniques Linearsweep voltammetry At low potential value

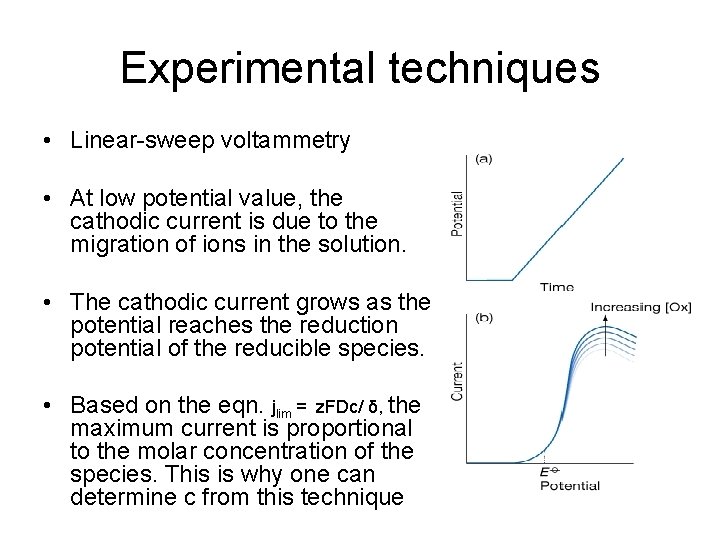
Experimental techniques • Linear-sweep voltammetry • At low potential value, the cathodic current is due to the migration of ions in the solution. • The cathodic current grows as the potential reaches the reduction potential of the reducible species. • Based on the eqn. jlim = z. FDc/ δ, the maximum current is proportional to the molar concentration of the species. This is why one can determine c from this technique

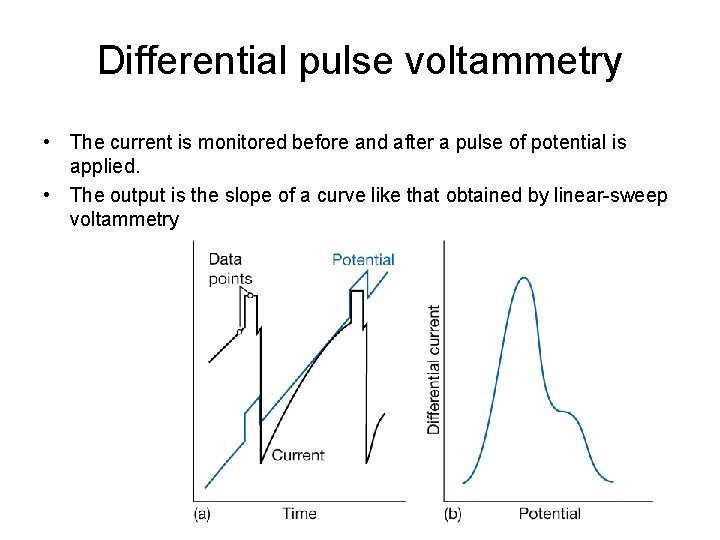
Differential pulse voltammetry • The current is monitored before and after a pulse of potential is applied. • The output is the slope of a curve like that obtained by linear-sweep voltammetry

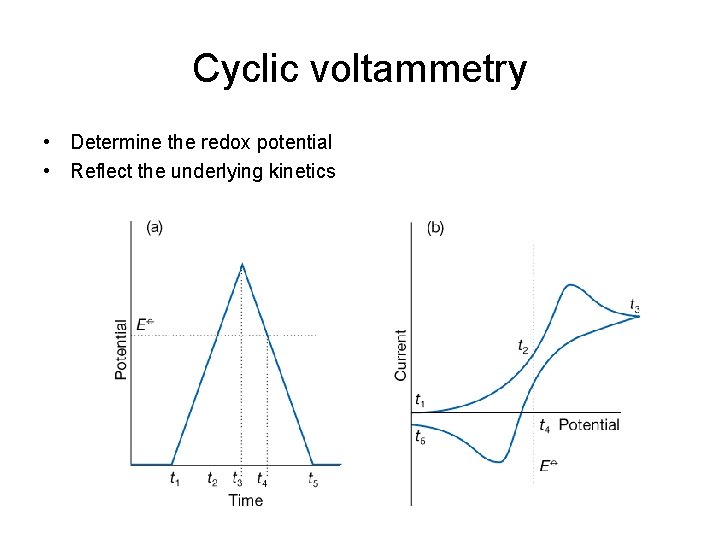
Cyclic voltammetry • Determine the redox potential • Reflect the underlying kinetics

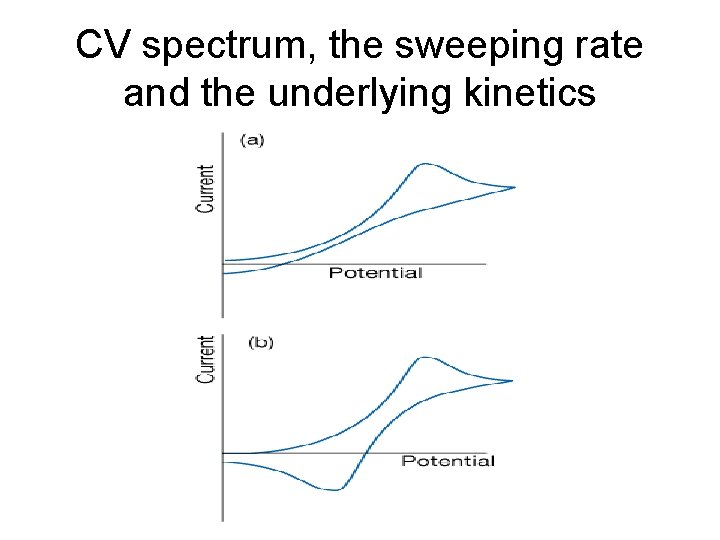
CV spectrum, the sweeping rate and the underlying kinetics

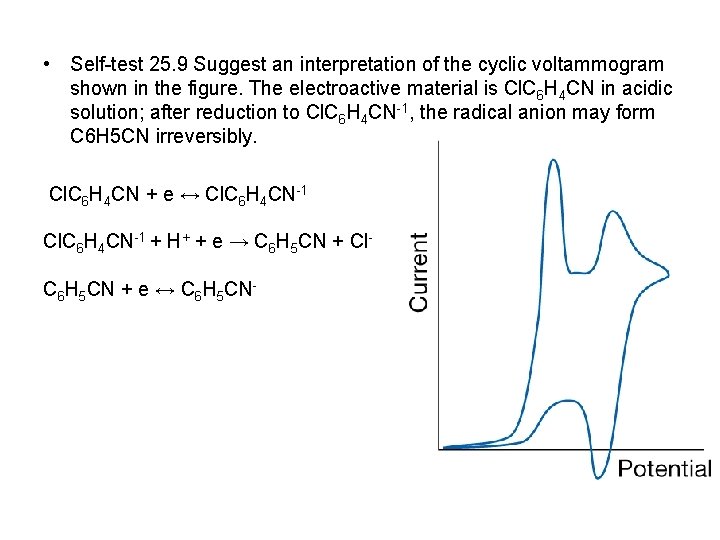
• Self-test 25. 9 Suggest an interpretation of the cyclic voltammogram shown in the figure. The electroactive material is Cl. C 6 H 4 CN in acidic solution; after reduction to Cl. C 6 H 4 CN-1, the radical anion may form C 6 H 5 CN irreversibly. Cl. C 6 H 4 CN + e ↔ Cl. C 6 H 4 CN-1 + H+ + e → C 6 H 5 CN + Cl. C 6 H 5 CN + e ↔ C 6 H 5 CN-

25. 11 Electrolysis • Cell overpotential: the sum of the overpotentials at the two electrodes and the ohmic drop due to the current through the electrolyte (IRs). • Electrolysis: To induce current to flow through an electrochemical cell and force a non-spontaneous cell reaction to occur. It requires that the applied potential difference exceed the zero-current potential by at least the cell overpotential. • Estimating the relative rates of electrolysis.

Working galvanic cells • In working galvanic cells, the overpotential leads to a smaller potential than under zero-current conditions. • The cell potential decreases as current is generated because it is then no longer working reversibly. • Consider the cell M|M+(aq)||M’+(aq)|M’ and ignore complications from liquid junctions. The potential of the cell E’ = ΔФR - ΔФL • As ΔФR = ER + ηR ; ΔФL = EL + ηL • E’ = E + ηR - ηL

• To emphasize that a working cell has a lower potential than a zerocurrent cell, we write • E’ = E - |ηR |- |ηL| One should also subtract the ohmic potential difference IRs E’ = E - |ηR |- |ηL| - IRs • The omhic term is a contribution to the cell’s irreversibility- it is a thermal dissipation. • E’ = E – IRs – 4 RT ln(I/9 Aj))/F j = (jo. Ljo. R)1/2 where jo. L and jo. R are the exchange current densities for the two electrodes (for single electron transfer and high overpotential) • The concentration overpotential also reduces the cell potential • see 25. 63 (8 th edition) or 29. 59 )7 th edition) • The full expression for the cell potential when a current I is being drawn: see eqn 25. 64 a or 29. 60

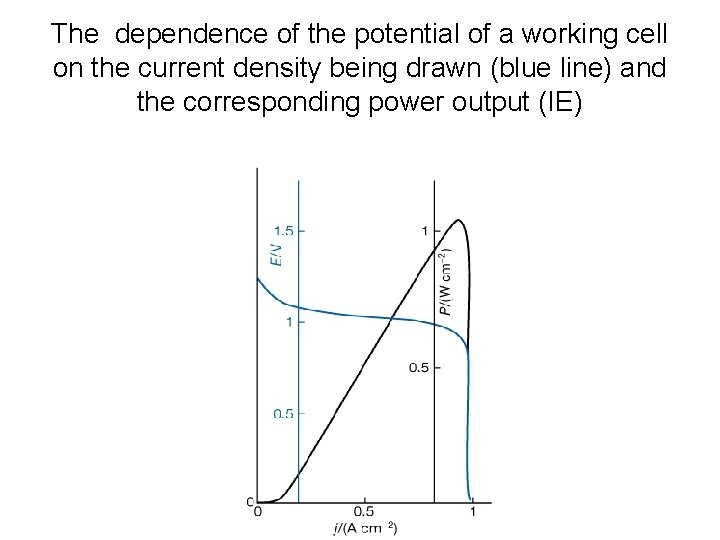
The dependence of the potential of a working cell on the current density being drawn (blue line) and the corresponding power output (IE)

Fuel Cells • Reactants are supplied from outside. • In hydrogen/oxygen cell, the electrolyte used is concentrated aqueous potassium hydroxide maintained at 200 o. C and 20 -40 atm. • The cathode reaction is O 2(g) + 2 H 2 O(l) + 4 e- → 4 OH-(aq) Eo = 0. 40 V • The anode reaction is oxidation H 2(g) + 2 OH-(aq) → 2 H 2 O(l) + 2 e • The overall reaction 2 H 2(g) + O 2(g) → 2 H 2 O(l) E = 1. 23 V • The advantage of the hydrogen/oxygen system is the large exchange current density of the hydrogen reaction, but the oxygen reaction has a small exchange current density.

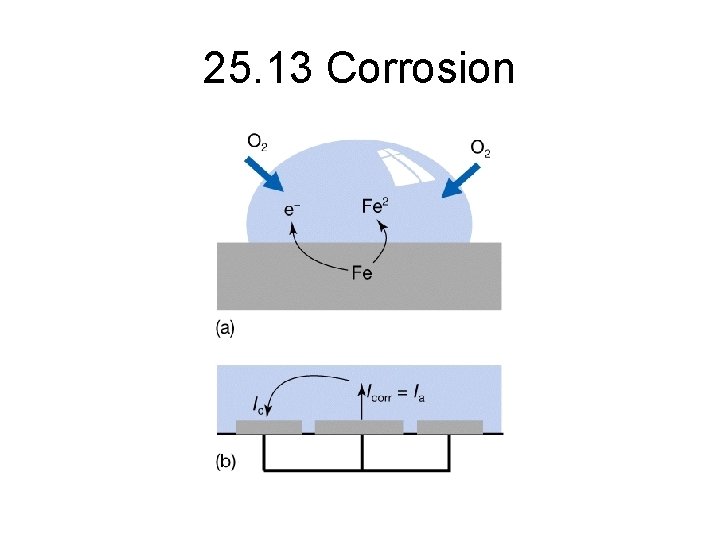
25. 13 Corrosion

• Consider the following half reactions: In acidic environment: (a) 2 H+(aq) + 2 e → H 2(g) Eo = 0 (b) 4 H+(aq) + O 2 + 4 e → 2 H 2 O(l) Eo = 1. 23 V In basic solution: (c) 2 H 2 O(l) + O 2(g) + 4 e → 4 OH-(aq) Eo = 0. 40 V • Consider the other half reaction: Fe 2+(aq) + 2 e → Fe(s) Eo = -0. 44 V • The potential difference suggests that iron can be oxidized under the above three conditions. • The thermodynamic discussion only indicates the tendency. The kinetic process shall also be examined.

• Self-test: The exchange current density of a Pt(s)|H 2(g)|H+(aq) electrode at 298 K is 0. 79 m. Acm-2. Calculate the current density when the over potential is +5. 0 m. V. What would be the current at p. H = 2. 0, the other conditions being the same? • Solution: Step 1: using Nernst equation to calculate E, Step 2: calculate η on the basis that there is no change in E’; η step 3: = E’ – E: J = j 0 fη

• 25. 23 b Suppose that the electrode potential is set at 0. 50 V. calculate the current density for the ratio of activities α(Cr 3+)/α(Cr 2+) in the range 0. 1 to 10. 0 and at 25 o. C.